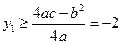(单词翻译:单击)
第一部分 选择题(共30分)
一、选择题:
1、比0大的数是( )
A -1 B 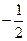 C 0 D 1
C 0 D 1

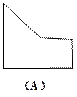
2、图1所示的几何体的主视图是( )





3、在6×6方格中,将图2—①中的图形N 平移后位置如图2—②所示,则图形N的平移方法中,正确的是( )
平移后位置如图2—②所示,则图形N的平移方法中,正确的是( )
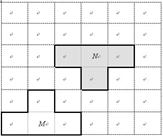

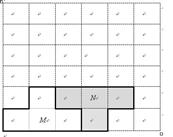
A 向下移动1格 B 向上移动1格 C 向上移动2格 D向 下移动2格
下移动2格

4、计算: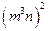 的结果是( )
的结果是( )
A 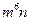 B
B 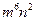 C
C 
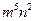 D
D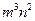

5、为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图3,该调查的方式是( ),图3中的a的值是( )

A 全面调查,26 B全面调查,24
C 抽样调查,26 D抽样调查,24

6、已知两数x,y之和是10,x比y的3倍大2,则下面所列方程组正确的是( )
A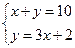 B
B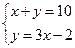
 C
C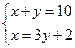 D
D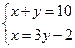

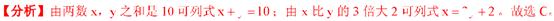
7、实数a在数轴上的位置如图4所示,则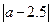 =( )
=( )
A 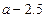 B
B 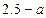 C
C 
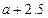 D
D 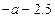


8、若代数式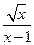 有意义,则实数x的取值范围是( )
有意义,则实数x的取值范围是( )
A 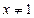 B
B 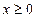 C
C 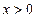 D
D 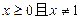

9、若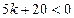 ,则关于x的一元二次方程
,则关于x的一元二次方程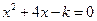 的根的情况是( )
的根的情况是( )
A 没有实数根  B有两个相等的实数根
B有两个相等的实数根
C 有两个不相等的实数根 D无法判断

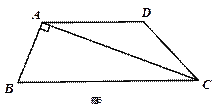
10、如图5,四边形ABCD是梯形,AD∥BC,CA是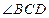 的平分线,且
的平分线,且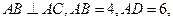 则
则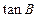 =( )
=( )
A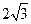 B
B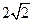 C
C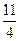 D
D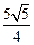

第二部分 非选择题(共120分)
二.填空题(本大题共6小题,每小题3分,满分18分)
11.点P在线段AB的垂直平分线上,PA=7,则PB=______________ .


12.广州某慈善机构全年共募集善款5250000元,将5250000用科学记数法表示为___________ .

13.分解因式: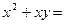 ___
___ ____________.
____________.

14.一次函数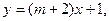 若
若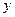 随
随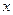 的增大而增大,则
的增大而增大,则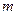 的取值范围是___________ .
的取值范围是___________ .

15.如图6,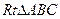 的斜边AB=16,
的斜边AB=16, 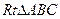 绕点O顺时针旋转后得到
绕点O顺时针旋转后得到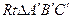 ,则
,则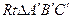 的斜边
的斜边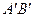 上的中线
上的中线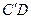 的长度为_____________ .
的长度为_____________ .


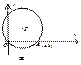
16.如图7,在平面直角坐标系中,点O为坐标原点,点P在第一象限,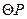 与
与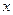 轴交于O,A两点,点A的坐标为(6,0),
轴交于O,A两点,点A的坐标为(6,0),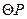 的半径为
的半径为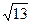 ,则点P的坐标为 ____________.
,则点P的坐标为 ____________.

三.解答题(本大题共9小题,满分10 2分,解答应写出文字说明,证明过程或演算步骤)
2分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分9分)
解方程:
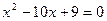 .
.

18.(本小题满分9分)
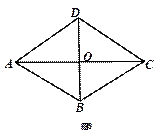
如图8,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.

19.(本小题满分10分)
先化简,再求值: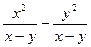 ,其中
,其中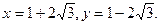

20.(本小题满分10分)
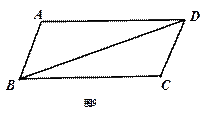
已知四边形ABCD是平行四边形(如 图9),把△ABD沿对角线BD翻折180°得到△AˊBD.
图9),把△ABD沿对角线BD翻折180°得到△AˊBD.
(1)利用尺规作出△AˊBD.(要求保留作图痕迹,不写作法);
(2)设D Aˊ 与BC交于点E,求证:△BAˊE≌△DCE.

21.(本小题满分12分)
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下:
11 10 6 15 9 16 13 12 0 8
2 8 10 17 6 13 7 5 7 3
12 10 7 11 3 6 8 14 15 12
(1) 求样本数据中为A级的频率;
(2) 试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3) 从样本数据为C级的人中随机抽取2人,用列举法求抽得2个人的“日均发微博条数”都是3的概率.



22.(本小题满分12分)
如图10, 在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.
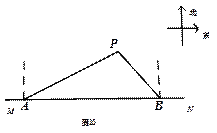
(1)求船P到海岸线MN的距离(精确到0.1海里);
(2)若船A、船B分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.


23.(本小题满分12分)
如图11,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数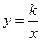 (x
(x >0,k≠0)的图像经过线段BC的中点D.
>0,k≠0)的图像经过线段BC的中点D.
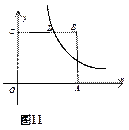
(1)求k的值;
(2)若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。



24.(本小题满分14分)
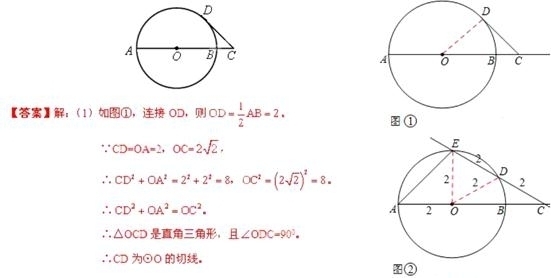
已知A B是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O 上运动(不与点B重合),连接CD,且CD=OA.
B是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O 上运动(不与点B重合),连接CD,且CD=OA.
(1)当OC=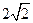 时(如图12),求证:CD是⊙O的切线;
时(如图12),求证:CD是⊙O的切线;
(2)当OC>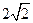 时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
①当D为CE中点时,求△ACE的周长;
②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE·ED的值;若不存在,请说明理由。


25、(本小题满分14分)
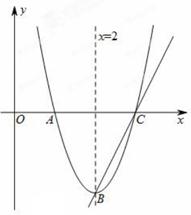
已知抛物线y1=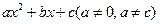 过点A(1,0),顶点为B,且抛物线不经过第三象限。
过点A(1,0),顶点为B,且抛物线不经过第三象限。
(1)使用a、c表示b;
(2)判断点B所在象限,并说明理由;
(3)若直线y2=2x+m经过点B,且于该抛物线交于另一点C(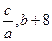 ),求当x≥1时y1的取值范围。
),求当x≥1时y1的取值范围。




2013广州中考数学参考答案:
一、DACBD, CBDAB
二、11、7 12、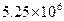 13、
13、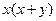
14、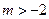 15、8 16、
15、8 16、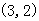
三、17、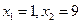
18、6
19、原式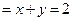
20、(1)画图略
(2)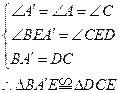
21、(1)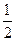 (2)500 (3)
(2)500 (3)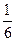
22、(1)15. (2)B船先到达
23、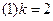 (2)
(2) 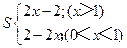
24(1)略 (2)① ②存在,两个,AE·ED=4
②存在,两个,AE·ED=4
25、(1)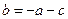
(2)B在第四象限。理由如下
∵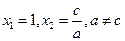
所以抛物线与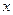 轴有两个交点
轴有两个交点
又因为抛物线不经过第三象限
所以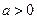 ,且顶点在第四象限
,且顶点在第四象限
(3)∵
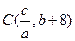 ,且在抛物线上,∴
,且在抛物线上,∴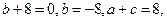
把B、C两点代入直线解析式易得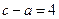
解得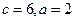
画图易知,C在A的右侧,
∴当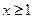 时,
时,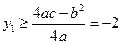
考点:一次函数,二次函数
难度:难
答案:
提示步骤:
(1)第(1)问经过A(1,0),把点代入函数即可得到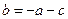
(2)第(2)问,判断点在哪个象限,需要根据题意画图,由条件:图像不经过第三象限就可以推出开口向上,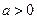 ,只需要知道抛物线与
,只需要知道抛物线与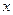 轴有几个交点即可解决
轴有几个交点即可解决
(3)判断与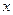 轴有两个交点,一个可以考虑△,由△就可以判断出与
轴有两个交点,一个可以考虑△,由△就可以判断出与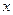 轴有两个交点,所以在第四象限;或者直接用公式法(或十字相乘法)算出,由两个不同的解
轴有两个交点,所以在第四象限;或者直接用公式法(或十字相乘法)算出,由两个不同的解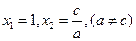 ,所以在第四象限
,所以在第四象限
(4)题目问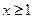 时,
时,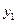 的取值范围,只要把图像画出来就清晰了,难点在于要观察出
的取值范围,只要把图像画出来就清晰了,难点在于要观察出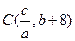 是抛物线与
是抛物线与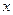 轴的另一个交点,理由是
轴的另一个交点,理由是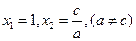 ,由这里可以发现,
,由这里可以发现,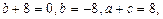 还可以发现C在A的右侧;可以确定直线经过B、C两点
还可以发现C在A的右侧;可以确定直线经过B、C两点
(5)看图像可以得到 ,
,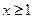 时,
时,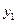 大于等于最小值,此时算出二次函数最小值即可,即求出
大于等于最小值,此时算出二次函数最小值即可,即求出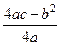 即可,已经知道
即可,已经知道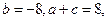 ,算出
,算出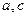 即可,即是要再找出一个与
即可,即是要再找出一个与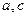 有关的式子,即可解方程组求出
有关的式子,即可解方程组求出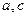
(6)直线经过B、C两点,把B、C两点坐标代入直线消去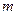 ,整理即可得到
,整理即可得到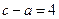
联立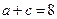 ,解得
,解得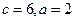 ,此时
,此时