(单词翻译:单击)
一、选择题(共12小题,每小题3分,满分36分)
1.(3分)(2014•崇左)下列实数是无理数 的是( )
的是( )
A.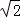 B. 1 C. 0 D. ﹣1
B. 1 C. 0 D. ﹣1
分析: 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答: 解:A、是无理数,选项正确;
B、是整数,是有理数,选项错误;
C、是整数,是有理数,选项错误;
D、是整数,是有理数,选项错误.
故选A.
点评: 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.(3分)(2014•崇左)如图,直线AB∥CD,如果∠1=70°,那么∠BOF的度数是( )
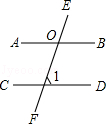
A. 70° B. 100° C. 110° D. 120°
考点: 平行线的性质.
分析: 由“两直线平行,同旁内角互补”进行计算.
解答: 解:如图,∵直线AB∥CD,
∴∠BOF+∠1=180°.
又∠1=70°,
∴∠BOF=110°.
故选:C.
点评: 本题考查了平行线的性质.熟记平行线的性质定理是解题的关键.
3.(3分)(2014•崇左)震惊世界的MH370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中,首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为( )
A. 4.5×102 B. 4.5×103 C. 45.0×102 D. 0.45×104
考点: 科学记数法— 表示较大的数.
表示较大的数.
分析: 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10, n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答: 解:将4500用科学记数法表示为:4.5×103.
故选B.
点评: 此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(3分)(2014•崇左)在2014年5月崇左市教育局举行的“经典诗朗诵”演讲比赛中,有11名学生参加决赛,他们决赛的成绩各不相同,其中的一名学生想知道自己能否进入前6名,不仅要了解自己的成绩,还要了解这11名学生成绩的( )
A. 众数 B. 中位数 C. 平均数 D. 方差
考点: 统计量的选择.
分析: 11人成绩的中位数是第6名的成绩.参赛选手要想知道自己是否能进入前6名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
解答: 解:由于总共有11个人,且他们的分数互不相同,第6的成绩是中位数,要判断是否进入前6名,故应知道中位数的多少.
故选:B.
点评: 此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
5.(3分)(2014•崇左)下列几何体的主视图、左视图、俯视图的图形完全相同的是( )
A. 三棱锥 B. 长方体 C. 三棱柱 D. 球体
考点: 简单几何体的三视图.
分析: 主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
解答: 解:A、三棱锥的主视图、左视图都是三角形,俯视图为三角形多一点,故本选项错误;
B、长方体的主视图为长方形、左视图为长方形或正方形、俯视图为长方形或正方形,故本选项错误;
C、三棱柱的主视图和左视图是一个矩形,俯视图是一个三角形,故本选项错误;
D、球体的主视图、左视图、俯视图都是圆形;故本选项正确;
故选:D.
点评: 本题考查三视图的有关知识,本题只要清楚了解各个几何体的三视图即可求解.
6.(3分)(2014•崇左)如果崇左市市区某中午的气温是37℃,到下午下降了3℃,那么下午的气温是( )
A. 40℃ B. 38℃ C. 36℃ D. 34℃
考点: 有理数的减法.
专题: 应用题.
分析: 用中午的温度减去下降的温度,然后根据有理数的减法运算法则进行计算即可得解.
解答: 解:37﹣3=34℃.
故选D.
点评: 本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.
7.(3分)(2014•崇左)若点A(2,4)在函数y=kx的图象上,则下列各点在此函数图象上的是( )
A. (1,2) B. (﹣2,﹣1) C. (﹣1,2) D. (2,﹣4)
考点: 一次函数图象上点的坐标特征.
分析: 直接把点A(2,4)代入函数y=kx求出k的值,再把各点代入函数解析式进行检验即可.
解答: 解:∵点A(2,4)在函数y=kx的图象上,
∴4=2k,解得k=2,
∴一次函数的解析式为y=2x,
A、∵当x=1时,y=2,∴此点在函数图象上,故本选项正确;
B、∵当x=﹣2时,y=﹣4≠﹣1,∴此点不在函数图象上,故本选项错误;
C、∵当x=﹣1时,y=﹣2≠2,∴此点不在函数图象上,故本选项错误;
D、∵当x=2时,y=4≠﹣4,∴此点不在函数图象 上,故本选项错误.
上,故本选项错误.
故选A.
点评: 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此 函数的解析式是解答此题的关键.
函数的解析式是解答此题的关键.
8.(3分)(2014•崇左)下列说法正确的是( )
A. 对角线相等的平行四边形是菱形
B. 有一组邻边相等的平行四边形是菱形
C. 对角线相互垂直的四边形是菱形
D. 有一个角是直角的平行四边形是菱形
考点: 菱形的判定.
分析: 利用菱形的判定定理对各个选项逐一判断后即可确定正确的选项.
解答: 解:A、对角线相等的平行四边形式矩形,错误;
B、正确;
C、对角线相互垂直的平行四边形是菱形,错误;
D、有一个角是直角的平行四边形是矩形,故错误,
故选B.
点评: 本题考查了菱形的判定,牢记菱形的判定定理是解答本题的关键,难度不大.
9.(3分)(2014•崇左)方程组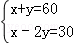 的解是( )
的解是( )
A.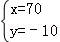 B.
B.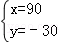 C.
C.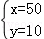 D.
D.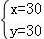
考点: 解二元一次方程组.
专题: 计算题.
分析: 方程组利用加减消元法求出解即可.
解答: 解: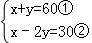 ,
,
①﹣②得:3y=30,即y=10,
将y=10代入①得:x+10=60,即x=50,
则方程组的解为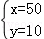 .
.
故选C
点评: 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
10.(3分)(2014•崇左)已知点A(a,2013)与点B(2014,b)关于x轴对称,则a+b的值为( )
A. ﹣1 B. 1 C. 2 D. 3
考点: 关于x轴、y轴对称的点的坐标.
分析: 首先根据关于x轴对称点的坐标特点得到A点坐标,再根据关于y轴对称点的坐标特点得到C点坐标即可.
解答: 解:∵A(a,2013)与点B(2014,b)关于x轴对称,
∴a=2014,b=﹣2013
∴a+b=1,
故答案选:B.
点评: 此题主要考查了关于x、y轴对称点的坐标特点,关键是掌握点的坐标的变化规律.
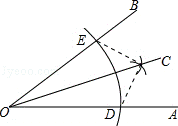
11.(3分)(2014•崇左)如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法 是( )
是( )
作法:
①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E;
②分别以D,E为圆心,大于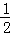 DE的长为半径画弧,两弧在∠AOB内交于一点C;
DE的长为半径画弧,两弧在∠AOB内交于一点C;
③画射线OC,射线OC就是∠AOB的角平分线.
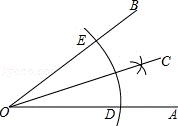
A. ASA B. SAS C. SSS D. AAS
考点: 作图—基本作图;全等三角形的判定.
分析: 根据作图的过程知道:OE=OD,OC=OC,CE=CD,所以由全等三角形的判定定理SSS可以证得△EOC≌△DOC.
解答: 解:如图,连接EC、DC.
根据作图的过程知,
在△EOC与△DOC中,
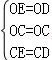 ,
,
△EOC≌△DO C(SSS).
C(SSS).
故选C.
点评: 本题考查了全等三角形的判定定理的应用,注意:三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.
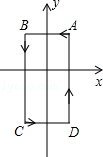
12.(3分)(2014•崇左)如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A. (﹣1,0) B. (1,﹣2) C. (1,1) D. (﹣1,﹣1)
考点: 规律型:点的坐标.
分析: 根据点的坐标求出四边形ABCD的周长,然后求出另一端是 绕第几圈后的第几个单位长度,从而确定答案.
绕第几圈后的第几个单位长度,从而确定答案.
解答: 解:∵A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),
∴AB=1﹣(﹣1)=2,BC=1﹣(﹣2)=3,CD=1﹣(﹣1)=2,DA=1﹣(﹣2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2014÷10=201…4,
∴细线另一端在绕四边形第202圈的第4个单位长度的位置,
即线段BC的中间位置,点的坐标为(﹣1,﹣1).
故选D.
点评: 本题利用点的坐标考查了数字变化规律,根据点的坐标求出四边形ABCD一周的长度,从而确定2014个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键.
二、填空题(本大题共6小题,每小题3分,满分18分)
13.(3分)(2014•崇左)若分式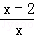 的值是0,则x的值为 2 .
的值是0,则x的值为 2 .
考点: 分式的值为零的条件.
分析: 根据分式的值为零的条件得到x﹣2=0且x≠0,易得x=2.
解答: 解:∵分式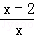 的值是0,
的值是0,
∴x﹣2=0且x≠0,
∴x=2.
故答案为:2.
点评: 本题考查了分式的值为零的条件:当分式的分母不为零,分子为零时,分式的值为零.
14.(3分)(2014•崇左)因式分解:x2﹣1= (x+1)(x﹣1) .
考点: 因式分解-运用公式法.
专题: 计算题.
分析: 方程利用平方差公式分解即可.
解答: 解:原式=(x+1)(x﹣1).
故答案为:(x+1)(x﹣1)
点评: 此题考查了因式分解﹣运用公式法,熟练掌握平方差公式是解本题的关键.
15.(3分)(2014•崇左)化简: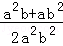 =
=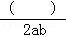 . a+b .
. a+b .
考点: 约分.
分析: 先将分式的分子因式分解,再约分,即可求解.
解答: 解: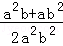 =
=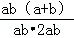 =
=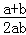 .
.
故答案为a+b.
点评: 本题考查了约分的定义:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、 分母的最大公因式并约去,注意不要忽视数字系数的约分.
分母的最大公因式并约去,注意不要忽视数字系数的约分.
16.(3分)(2014•崇左)已知在一个样本中,50个数据分别落在5个组内,第一,二,三,四,五组数据的个数分别是2,8,15,20,5,则第四组频数为 20 .
考点: 频数与频率.
分析: 根据各小组频数之和等于数据总和,进行计算.
解答: 解:根据题意,得
第四组频数为第4组数据个数,故第四组频数为20.
故答案为:20.
点评: 本题是对频率、频数灵活运用的综合考查.
注意:各小组频数之和等于数据总和,各小组频率之和等于1.
17.(3分)(2014•崇左)已知直角三角形的两条直角边长为6,8,那么斜边上的中线长是 5 .
考点: 直角三角形斜边上的中线;勾股定理.
分析: 利用勾股定理列式求出斜边,再根据直角三角形斜边上的中线等于斜边的一半解答.
解答: 解:由勾股定理得,斜边=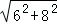 =10,
=10,
所以,斜边上的中线长=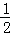 ×10=5.
×10=5.
故答案为:5.
点评: 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,勾股定理,熟记性质是解题的关键.
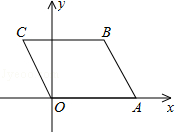
18.(3分)(2014•崇左)如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 y=﹣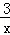 .
.
考点: 待定系数法求反比例函数解析式;平行四边形的性质.
专题: 计算题;待定系数法.
分析: 设经过C点的反比例函数的解析式是y=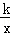 (k≠0),设C(x,y).根据平行四边形的性质求出点C的坐标(﹣1,3).然后利用待定系数法求反比例函数的解析式.
(k≠0),设C(x,y).根据平行四边形的性质求出点C的坐标(﹣1,3).然后利用待定系数法求反比例函数的解析式.
解答: 解:设经过C点的反比例函数的解析式是y=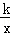 (k≠0),设C(x,y).
(k≠0),设C(x,y).
∵四边形OABC是平行四边形,
∴BC∥OA,BC=OA;
∵A(4,0),B(3,3),
∴点C的纵坐标是y=3,|3﹣x|=4(x<0),
∴x=﹣1,
∴C(﹣1,3).
∵点C在反比例函数y=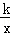 (k≠0)的图象上,
(k≠0)的图象上,
∴3=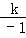 ,
,
解得,k=﹣3,
∴经过C点的反比例函数的解析式是y=﹣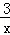 .
.
故答案是:y=﹣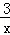 .
.
点评: 本题主要考查了平行四边形的性质(对边平行且相等)、利用待定系数法求反比例函数的解析式.解答反比例函数的解析式时,还借用了反比例函数图象上点的坐标特征,经过函数的某点一定在函数的图象上.
三、解答题(本大题共8小题,满分66分)
19.(6分)(2014•崇左 )计算:(
)计算:(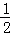 )﹣1﹣20140﹣2sin30°+
)﹣1﹣20140﹣2sin30°+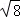 .
.
考点: 实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.
分析: 原式第一项利用负指数幂法则计算,第二项利用零指数幂法则计算,第三项利用特殊角的三角函数值计算,最后一项化为最简二次根式,计算即可得到结果.
解答: 解:原式=2﹣1﹣2×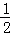 +2
+2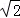 =2﹣1﹣1+2
=2﹣1﹣1+2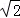 =2
=2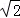 .
.
点评: 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
20.(6分)(2014•崇左)解不等式2x﹣3<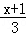 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
考点: 解一元一次不等式;在数轴上表示不等式的解集.
专题: 计算题.
分析: 先去分母,再去括号、移项、合并同类项,系数化为1,求出不等式的解集,再在数轴上表示出来即可.
解答: 解:3 (2x﹣3)<x+1
(2x﹣3)<x+1
6x﹣9<x+1
5x<10
x<2
∴原不等式的解集为x<2,
在数轴上表示为:
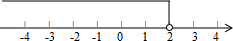
点评: 本题考查了解简单不等式的能力,解答这类题学生往往在解题 时不注意移项要改变符号这一点而出错.
时不注意移项要改变符号这一点而出错.
21.(6分)(2014•崇左)写出下列命题的已知、求证,并完成证明过程.
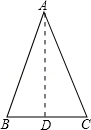
命题:如果一个三角形的两个角相等,那么这两个角所对的边也相等(简称:“等角对等边”).
已知:如图, 在△ABC中,∠B=∠C .
求证: AB=AC .
证明:

考点: 命题与定理;等腰三角形的性质.
专题: 证明题.
分析: 根据图示,分析原命题,找出其条件与结论,然后根据∠B=∠C证明△ABC为等腰三角形,从而得出结论.
解答: 解:在△ABC中,∠B=∠C,
AB=AC,
证明:过点A作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
在△ABD和△ACD中,
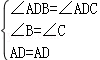
∴△ABD≌△ACD(AAS),
∴AB=AC.
点评: 本题主要考查学生对命题的定义的理解,难度适中.
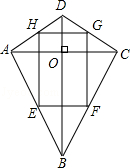
22.(8分)(2014•崇左)如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形.
考点: 中点四边形.
专题: 证明题.
分析: 首先利用三角形的中位线定理证得四边形EFGH为平行四边形,然后利用有一个角是直角的平行四边形是矩形判定即可.
解答: 证明:∵点E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=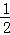 AC,GH=
AC,GH= AC,
AC,
∴EF=GH,同理EH FG
∴四边形EFGH是平行四边形;
又∵对角线AC、BD互相垂直,
∴EF与FG垂直.
∴四边形EFGH是矩形.
点评: 本题考查了中点四边形的知识,解题的关键是灵活运用三角形的中位线定理,平行四边形的判断及矩形的判断进行证明,是一道综合题.
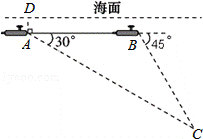
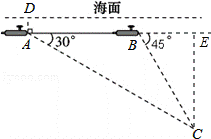
23.(8分)(2014•崇左)中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为 30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据
30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据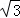 ≈1.732)
≈1.732)
考点: 解直角三角形的应用-仰角俯角问题.
分析: 过点C作CE⊥AB交AB延长线于E,设CE=x,在Rt△BCE和Rt△ACE中分别用x表示BE和AE的长度,然后根据AB+BE=AE,列出方程求出x的值,继而可判断“蛟龙”号能在保证安全的情况下打捞海底黑匣子C.
解答: 解:过点C作CE⊥AB交AB延长线于E,
设CE=x,
在Rt△BCE中,∵∠CBE=45°,
∴BE=CE=x,
在Rt△ACE中,∵∠CAE=30°,
∴AE=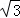 x,
x,
∵AB+BE=AE,
∴3000+x=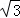 x,
x,
解得:x=1500(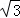 +1)≈4098(米),
+1)≈4098(米),
显然2000+4098=6098<7062.68,
所以“蛟龙”号能在保证安全的情况下打捞海底黑匣子.
点评: 本题考查俯角的定义,以及解直角三角形的实际应用问题.此题难度不大,解题的关键是要求学生能借助俯角构造直角三角形并解直角三角形,注意当两个直角三角形有公共边时,利用这条公共边进行求解是解此类题的常用方法.
24.(10分)(2014•崇左)在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小、质地完全相同,小李从布袋里随机取出一个小球,记下数字为x,小张在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=﹣x+5图象上的概率.
考点: 列表法与树状图法;一次函数图象上点的坐标特征.
分析: (1)首先根据题意画出表格,即可得到Q的所以坐标;
(2)然后由表格求得所有等可能的结果与数字x、y满足y=﹣x+5的情况,再利用概率公式求解即可求得答案
解答: 解:列表得:
y
x
(x,y) 1 2 3 4
1 (1,2) (1,3) (1,4)
2 (2,1) (2,3) (2,4)
3 (3,1) (3,2) (3,4)
4 (4,1) (4,2) (4,3)
(1)点Q所有可能的坐标有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种;
(2)∵共有12种等可能的结果,其中在函数y=﹣x+5图象上的有4种,
即:(1,4),(2,3),(3,2),(4,1)
∴点P(x,y)在函数y=﹣x+5图象上的概率为:P=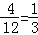 .
.
点评: 此题考查的是用列表法或树状图法求概率与不等式的性质.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
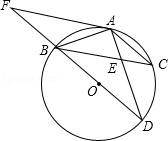
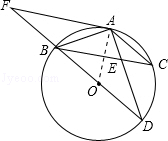
25.(10分)(2014•崇左)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.
(1)求证:∠ABC=∠D;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
考点: 切线的判定;圆周角定理;相似三角形的判定与性质.
专题: 计算题.
分析: (1)由AB=AC,利用等边对等角得到∠ABC=∠C,再由同弧所对的圆周角相等得到∠C=∠D,等量代换即可得证;
(2)由(1)的结论与公共角相等,得到三角形ABE与三角形ADB相似,由相似得比例,即可求出AB的长;
(3)直线FA与圆O相切,理由为:连接OA,由BD为直径,得到∠BAD为直角,在直角三角形ABD中,利用勾股定理求出BD的长,得到AB=OB=OA,根据BF=BO,得到AB等于FO的一半,确定出∠OAF为直角,即可得证.
解答: (1)证明:∵AB=AC,
∴∠ABC=∠C,
∵∠C与∠D都对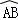 ,
,
∴∠C=∠D,
∴∠ABC=∠D;
(2)解:∵∠ABC=∠D,∠BAE=∠DAB,
∴△ABE∽△ADB,
∴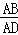 =
=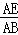 ,即AB2=AE•(AE+ED)=3,
,即AB2=AE•(AE+ED)=3,
解得:AB=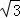 ;
;
(3)答:直线FA与圆O相切.理由如下:
连接OA,
∵BD为圆O的直径,
∴∠BAD=90°,
在Rt△ABD中,AB=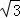 ,AD=1+2=3,
,AD=1+2=3,
根据勾股定理得:BD=2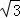 ,
,
∴OB=OA=AB=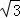 ,
,
∵BF=OB,
∴ AB=FB=OB,即AB=
AB=FB=OB,即AB=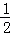 OF,
OF,
∴∠OAF=90°,
则直线AF与圆O相切.
点评: 此题考查了切线的判定,圆周角定理,以及相似三角形的判定与性质,熟练掌握切线的判定方法是解本题的关键.
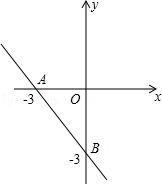
26.(12分)(2014•崇左)在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
考点: 二次函数综合题.
分析: (1)利用待定系数法求出解析式,
(2)先表示出二次函数y=x2+mx+n图象的顶点,利用直线AB列出式子,再与点A在二次函数上得到的式子组成方程组求得m,n的值,
(3)本题要分三种情况①当对称轴﹣3<﹣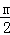 <0时,②当对称轴﹣
<0时,②当对称轴﹣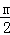 >0时,③当对称轴﹣
>0时,③当对称轴﹣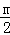 =0时,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
=0时,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
解答: 解:(1)A(﹣3,0),B(0,﹣3)代入y=kx+b得
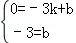 ,解得
,解得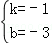 ,
,
∴一次函数y=kx+b的解析式为:y=﹣x﹣3;
(2)二次函数y=x2+mx+n图象的顶点为(﹣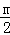 ,
,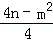 )
)
∵顶点在直线AB上,
∴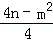 =
=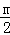 ﹣3,
﹣3,
又∵二次函数y=x2+mx+n的图象经过点A(﹣3,0),
∴9﹣3m+n=0,
∴组成方程组为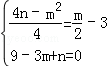
解得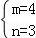 或
或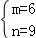 .
.
(3)∵二次函数y=x2+mx+n的图象经过点A.
∴9﹣3 m+n=0,
m+n=0,
∵当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,
①如图1,当对称轴﹣3<﹣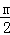 <0时
<0时
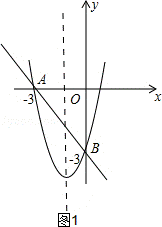
最小值为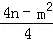 =﹣4,与9﹣3m+n=0,组成程组为
=﹣4,与9﹣3m+n=0,组成程组为
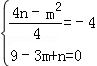 解得
解得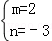 或
或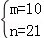 (由﹣3<﹣
(由﹣3<﹣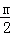 <0知不符合题意舍去)
<0知不符合题意舍去)
所以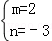 .
.
②如图2,当对称轴﹣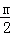 >0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,
>0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,
把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入与9﹣3m+n=0,得m=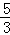 .
.
∵﹣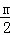 >0,
>0,
∴m<﹣2,
∴此种情况不成立,
③当对称轴﹣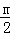 =0时,y=x2+mx+n的最小值为﹣4,
=0时,y=x2+mx+n的最小值为﹣4,
把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入与9﹣3m+n=0,得m=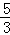 .
.
∵﹣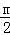 =0,
=0,
∴m=0,
∴此种情况不成立,
综上所述m=2,n=﹣3.
点评: 本题主要考查了二次函数综合题,解题的关键是在讨论对称轴不同位置得出m,n的值时,要结合对称轴看结果是否符合题意.


