(单词翻译:单击)
一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.计算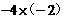 的结果是【 】
的结果是【 】
A. 8 B. 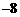 C. 6 D.
C. 6 D. 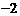

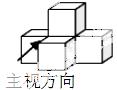
2.如图,由相同的 小正方体搭成的几何体的主视图是【 】
小正方体搭成的几何体的主视图是【 】


3.如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为【 】
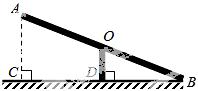
A. 25cm B. 50cm C. 75cm D. 1 00cm
00cm

考点:三角形中位线定理.
4.下列整数中,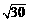 与最接近的是【 】
与最接近的是【 】
A. 4 B. 5 C. 6 D. 7

考点:估计无理数的大小.
5.从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是【 】

【答案】B
【解析】
试题分析:∵根据圆周角定理:直径所对的圆周角等于直角,
∴从所给直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是B.
故选B.
考点:圆周角定理.
6.某品牌电插座抽样检查的合格率为99%,则下列说法中正确的是【 】
A. 购买1 00个该品牌的电插座,一定有99个合格
00个该品牌的电插座,一定有99个合格
B. 购买1 00个该品牌的电插座,一定有99个合格
00个该品牌的电插座,一定有99个合格
C. 购买20个该品牌的电插座,一定都合格
D. 即使购买1个该品牌的电插 座,也可能不合格
座,也可能不合格

考点:概率的意义.
7.将分式方程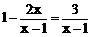 去分母,得到正确的整式方程是【 】
去分母,得到正确的整式方程是【 】
A. 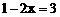 B.
B. 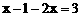 C.
C. 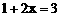 D.
D. 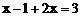

考点:去分母法则.
8.如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位∶m/s)与运动时间t(单位s)关系的函数图像中,正确的是【 】
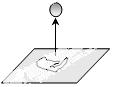


9.如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,连接BE,BF,则∠EBF的度数是【 】
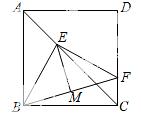
A. 45° B. 50° C. 60° D. 不确定

故选A.
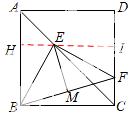
考点:1.单动点和定值问题;2.正方形的性质;3 .线段垂直平分线的性质;4.角平分线的性质;5.全等三角形的判定与性质;6.等腰直角三角形的判定和性质.
.线段垂直平分线的性质;4.角平分线的性质;5.全等三角形的判定与性质;6.等腰直角三角形的判定和性质.
10.如图,菱形ABCD的对角线AC= 4cm,把它沿着对角线AC方向平移1cm,得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为【 】
4cm,把它沿着对角线AC方向平移1cm,得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为【 】
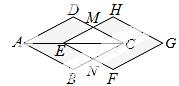
A. 4∶3 B. 3∶2 C. 14∶9 D. 17∶9

考点:1.面动平移问题;2.菱形的性质;3.平移的性质;4.相似三角形的判定和性质;5.转换思想的应用.
二、填空题(本题有6小题,每小题5分,共30分)
11.计算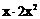 的结果是___________.
的结果是___________.

考点:单项式乘单项式.
12.如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是_________.
【答案】55°.
【解析】
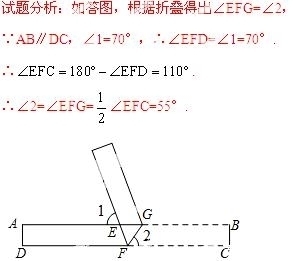
考点:1.翻折变换(折叠问题);2.平行线的性质;3.平角定义.
13.因式分解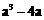 的结果是_________.
的结果是_________.

考点:提公因式法和应用公式法因式分解.
14.抽屉里放着黑白两种颜色的袜子各1双(除颜色外其余都相同)在看不见的情况下随机摸出两只袜子,他们恰好同色的概率是_________.

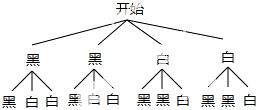
∵共有12种等可能的结果,它们恰好同色的有4种情况,
∴它们恰好同色的概率是: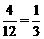 .
.
考点:1.列表法或树状图法;2.概率.
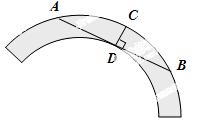
15.如图是一个古代车轮的碎片,小时为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆与点C,测得CD=10cm,AB=60cm,则这个外圆半径为 _________ cm.
【答案】50.
【解析】

考点:1.切线的性质;2.垂径定理;3.勾股定理;4.方程思想的应用.
16.有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下∶

则第n次的运算结果= _________ (含字母x和n的代数式表示).
【答案】 .
.
【解析】

考点:1.探索规律题(数字的变化类);2.分式的混合运算.
三、解答题(本题有8小题,第17-20每题8分,第21题10分,第22,23每题12分,第24题14分,共80分)
17.计算∶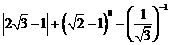

18.解不等式组∶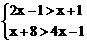 ,并把解集在下面数轴上表示出来.
,并把解集在下面数轴上表示出来.
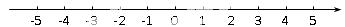
【答案】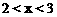 .
.
【解析】


考点:1.解一元一次不等式组;2. 在数轴上表示不等式组的解集.
19.已知反比例函数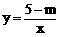 ,当x=2时y=3.
,当x=2时y=3.
(1)求m的值;
(2)当3≤x≤6时,求函数值y的取值范围.


考点:1.反比例函数的性质;2.曲线上点的坐标与方程的关系.
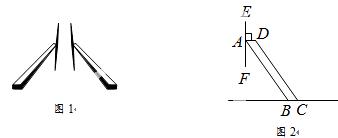
20.如图1是某公共汽车前挡风玻璃的雨刮器,其工作原理如图2,雨刷EF丄AD,垂足为A,AB=CD,且AD=BC.这样能使雨刷EF在运动时.始终垂直于玻璃窗下沿BC.请证明这一结论.
【答案】证明见解析.
【解析】

考点:1.阅读理解型问题;2. 平行四边形的判定和性质.
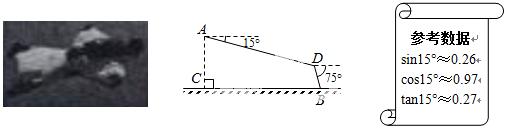
21.如图,某翼装飞行运动员从离水平地面高AC=500m的A处出发,沿着俯角为 15°的方向,直线滑行1600
15°的方向,直线滑行1600 米到达D点,然后打开
米到达D点,然后打开 降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离(结果精确到1m).
降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离(结果精确到1m).
【答案】1575m.
【解析】
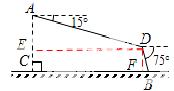
试题分析:首先过点D作DE⊥AC于点E,过点D作DF⊥BC于点F,进而里锐角三角函数关系得出DE 、
、
∴BC=CF+BF=1552+22.68=1574.68≈1575(m).
答:他飞行的水平距离为1575m.
考点:1.解直角三角形的应用(仰角俯角问题);2.锐角三角函数定义.
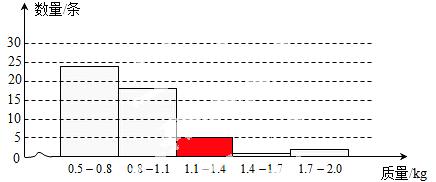
22.为了估计鱼塘中成品鱼(个体质最在0.5kg及以上,下同〉的总质量,先从鱼塘中捕捞50条成品鱼.称得它们的质量如下表∶
质量/kg | 0.5 | 0.6 | 0.7 | 1.0 | 1.2 | 1.6 | 1.9 |
数量/条 | 1 | 8 | 15 | 18 | 5 | 1 | 2 |
然后做上记号再放回水库中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
(1)请根据表中数据补全下面的直方图(各组中数据包括左端点不包括右端点).
(2)根据图中数据分组,估计从鱼塘中随机捕一条成 品鱼,其质量落在哪一组的可能性最大?
品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里 质量中等的成品鱼,其质量落在哪一组内?
质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).


(2)由题意,得

(4)设鱼塘中成品鱼的总质量为x,由题意,得
50:x=2:100,解得:x=2500.
∵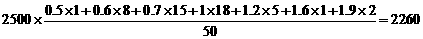 ,
,
∴估计鱼塘中成品鱼的总质量为2260kg.
考点:1.统计表;2.频数分布直方图;3.频数、频率和总量的关系;4.中位数;5.用样本估计总体.
23.某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销 售,B类杨梅深加工再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均
售,B类杨梅深加工再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均 销售价格y(单位∶万元/吨)与销售数
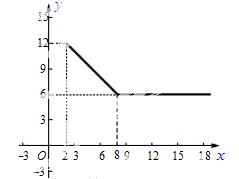
销售价格y(单位∶万元/吨)与销售数 量x(x≥2)(单位∶吨)之间的函数关系式如图,B类杨梅深加工总费用s(单位:万元)与加工数量t(单位∶吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
量x(x≥2)(单位∶吨)之间的函数关系式如图,B类杨梅深加工总费用s(单位:万元)与加工数量t(单位∶吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)直接写出A类杨 梅平均销售价格y与销售量x这间的函数关系式;
梅平均销售价格y与销售量x这间的函数关系式;
(2)第一次,该公司收购了20吨杨梅,其中A类杨梅 x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收人-经营
x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收人-经营 总成本).
总成本).
①求w关于x的函数关系式;
 ②若该公司获得了30万元毛利润,问∶用于直销的A类杨梅有多少吨?
②若该公司获得了30万元毛利润,问∶用于直销的A类杨梅有多少吨?
(3)第二次该公司准备投人132万元资金,请设计-种经营方案,使公司获得最大毛利润,并求出最大毛利润.
【答案】(1)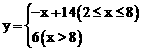 ;(2)①
;(2)①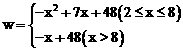 ;②18;(3)设计方案为:
;②18;(3)设计方案为:
(2)①分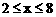 和
和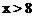 两种情况,根据毛利润=销售总收人-经营
两种情况,根据毛利润=销售总收人-经营 总成本列式即可.
总成本列式即可.

经营A类杨 梅所获得的毛利润为
梅所获得的毛利润为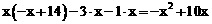 ,
,
经营B类杨 梅所获得的毛利润为
梅所获得的毛利润为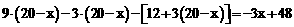 ,
,
∴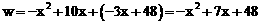 .
.
当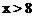 时
时 ,
,
经营A类杨 梅所获得的毛利润为
梅所获得的毛利润为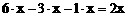 ,
,
经营B类杨 梅所获得的毛利润为
梅所获得的毛利润为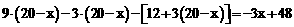 ,
,

经营A类杨 梅所获得的毛利润为
梅所获得的毛利润为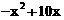 ,
,
经营B类杨 梅所获得的毛利润为
梅所获得的毛利润为
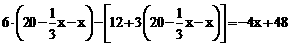 ,
,
∴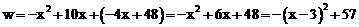 .
.
∴当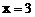 时,
时,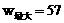 .
.
②当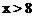 时,
时,
 考点:1
考点:1 阅读理解和方案型问题;2..一、二次函数和方程的应用;3.由实际问题列函数关系式;4.待定系数法的应用;5. 一、二次函数的性质;6.分类思想的应用.
阅读理解和方案型问题;2..一、二次函数和方程的应用;3.由实际问题列函数关系式;4.待定系数法的应用;5. 一、二次函数的性质;6.分类思想的应用.
24.研究几何图形,我们往往先给出这类图形的 定义,再研究它的性质和判定.
定义,再研究它的性质和判定.
定义∶六个内角相等的六边形叫等角六边形.
(1)研究 性质
性质
①如图1,等角六边形ABCDEF中,三组正对边AB与 DE,BC与EF,CD与AF分别有什么位置关系?证明你的结论.
DE,BC与EF,CD与AF分别有什么位置关系?证明你的结论.
②如图2,等角六边形ABCDEF中,如果有AB=DE,则其余两组正对边BC与EF,CD与AF相等吗?证明你的结论.
③如图3,等角六边形ABCDEF中.如果三条正对角线AD,BE,CF相交于一点O,那么三组正对边AB与DE,BC与EF,CD与AF分别有什么数量关系?证明你的结论.
(2)探索判定
三组正对边分别平行的六边形,至少需要几个内角为120°才能保证该六变形—定是等角六边形?
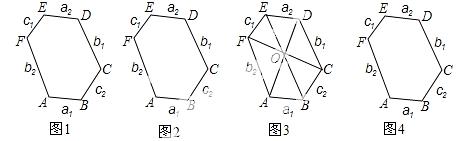
【答案】(1)①AB∥DE,BC∥EF,CD∥A F,证明见解析;② EF=BC,AF=DC
F,证明见解析;② EF=BC,AF=DC ,证明见解析;③AB=DE,AF=DC,EF=BC,证明证明见解析;(2)3.
,证明见解析;③AB=DE,AF=DC,EF=BC,证明证明见解析;(2)3.
【解析】

∵六边形ABCDEF是等角六边形,∴∠BAF=∠F=∠E=∠EDC=∠C=∠B=(6−2)•180° 6 =120°.
∵∠DAF+∠F+∠E+∠EDA=360°,∴∠DAF+∠EDA=360°-120°-120°=120°.
∵∠DAF+∠DAB=120°,∴∠DAB=∠EDA.∴AB∥DE.
同理BC∥EF,CD∥AF.
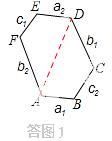
②结论:EF=BC,AF=DC.证明如下:
如 答图2,连接AE、DB,
答图2,连接AE、DB,
∵AB∥DE,AB=DE,∴四边形ABDE是平行四边形.∴AE=DB,∠EAB=∠BDE.
∵∠BAF=∠EDC. ∴∠FAE=∠CDB.
∴∠FAE=∠CDB.
在△AFE和△DCB中,∵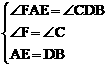 ,∴△AFE≌△DCB.∴EF=BC,AF=DC.
,∴△AFE≌△DCB.∴EF=BC,AF=DC.
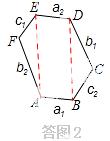
③结论:AB=DE,AF=DC,EF=BC.证明如下:

同理: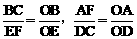 .
.
∴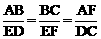 .
.
∴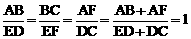 .∴AB=ED,AF=DC,EF=BC.
.∴AB=ED,AF=DC,EF=BC.
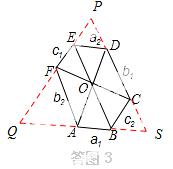
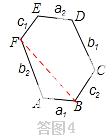
(2)如答图4,连接BF,
∵BC∥EF,∴∠CBF+∠EFB=180°.
∵∠A+∠ABF+∠AFB=1 80°,
80°,
∴∠ABC+∠A+∠AFE=360°.
同理:∠A+∠ABC+∠C=360°.∴∠AFE=∠C.
同理:∠A= ∠D,∠ABC=∠E.
∠D,∠ABC=∠E.
Ⅰ.若只有1个内角等于120°,不能保证该六边形一定是等角六边形.

∴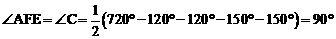 .
.
此时该六边形不是等角六边形.
Ⅲ.若有3个内角等于120°,能保证该六边形一定是等角六边形.
设∠A=∠D=α,∠ABC=∠E=β,∠AFE=∠C=γ.则2α+2β+2γ=720°.
∴α+β+γ=360°.
∵有3个内角等于120°,∴α、β、γ中至少有两个为120°.
若α、β、γ都等于120°,则六个内角都等于120°;
若α、β、γ中有两个为120°,根据α+β+ γ=360°可得第三个也等于120°,则六个内角都等于120°.
γ=360°可得第三个也等于120°,则六个内角都等于120°.
综上所述:若有3个内角等于120°,能保证该六边形一定是等角六边 形.
形.

考点:1.新定义和探究型问题;2.四边形综合题;3.全等三角形的判定和性质;4.多边形内角与外角;5.平行四边形的判定和性质;6.相似三角形的判定与性质;7.分类思想的应用.


