(单词翻译:单击)
一、选择题(共12小题,每小题3分,满分36分)
1.(3分)(2013• 德州)下列计算正确的是( )
A. 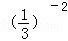 =9 B.
=9 B. 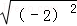 =﹣2 C. (﹣2)0=﹣1 D. |﹣5﹣3|=2
=﹣2 C. (﹣2)0=﹣1 D. |﹣5﹣3|=2
考点: 负整数指数幂;绝对值;算术平方根;零指数幂.
分析: 对各项分别进行负整数指数幂、算术平方根、零指数幂、绝对值的化简等运算,然后选出正确选项即可.
解答: 解:A、()﹣2=9,该式计算正确,故本选项正确;
B、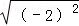 =2,该式计算错误,故本选项错误;
=2,该式计算错误,故本选项错误;
C、(﹣2)0=1,该式计算错误,故本选项错误;
D、|﹣5﹣3|=8,该式计算错误,故本选项错误;
故选A.
点评: 本题考查了负整数指数幂、算术平方根、零指数幂、绝对值的化简等运算,属于基础题,掌握各知识点运算法则是解题的关键.
2.(3分)(2013• 德州)民族图案是数学文化中的一块瑰宝.下列图案中,既不是中心对称图形也不是轴对称图形的是( )
A. 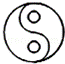 B.
B.  C.
C.  D.
D. 
考点: 中心对称图形;轴对称图形.
分析: 根据轴对称图形与中心对称图形的概念求解.
解答: 解:A、不是轴对称图形,是中心对称图形,故本选项错误;
B、是轴对称图形,也是中心对称图形,故本选项错误;
C、不是轴对称图形,也不是中心对称图形,故本选项正确;
D、是轴对称图形,也是中心对称图形,故本选项错误.
故选C.
点评: 本题考查了中心对称及轴对称的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
3.(3分)(2013• 德州)森林是地球之肺,每年能为人类提供大约28.3亿吨的有机物.28.3亿吨用科学记数法表示为( )
A. 28.3×107 B. 2.83×108 C. 0.283×1010 D. 2.83×109
考点: 科学记数法—表示较大的数.
分析: 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答: 解:28.3亿=28.3×108=2.83×109.
故选D.
点评: 此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(3分)(2013• 德州)如图,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为( )
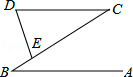
A. 68° B. 32° C. 22° D. 16°
考点: 平行线的性质;等腰三角形的性质.
分析: 根据等腰三角形两底角相等求出∠C的度数,再根据两直线平行,内错角相等解答即可.
解答: 解:∵CD=CE,
∴∠D=∠DEC,
∵∠D=74°,
∴∠C=180°﹣74°×2=32°,
∵AB∥CD,
∴∠B=∠C=32°.
故选B.
点评: 本题考查了两直线平行,内错角相等的性质,等腰三角形两底角相等的性质,熟记性质是解题的关键.
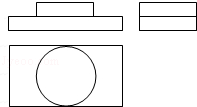
5.(3分)(2013• 德州)图中三视图所对应的直观图是( )
A. 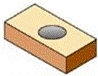 B.
B. 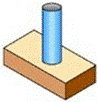 C.
C. 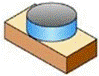 D.
D. 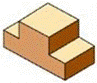
考点: 由三视图判断几何体.
分析: 主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
解答: 解:从俯视图可以看出直观图的下面部分为长方体,上面部分为圆柱,且与下面的长方体的顶面的两边相切高度相同.
只有C满足这两点.
故选C.
点评: 本题考查了三视图的概念.易错易混点:学生易忽略圆柱的高与长方体的高的大小关系,错选B.
6.(3分)(2013• 德州)甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是( )
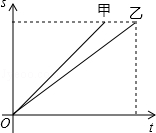
A. 甲、乙两人的速度相同 B. 甲先到达终点
C. 乙用的时间短 D. 乙比甲跑的路程多
考点: 函数的图象.
分析: 利用图象可得出,甲,乙的速度,以及所行路程等,注意利用所给数据结合图形逐个分析.
解答: 解:结合图象可知:两人同时出发,甲比乙先到达终点,甲的速度比乙的速度快,
故选B.
点评: 本题考查了函数的图象,关键是会看函数图象,要求同学们能从图象中得到正确信息.
7.(3分)(2013• 德州)下列命题中,真命题是( )
A. 对角线相等的四边形是等腰梯形
B. 对角线互相垂直平分的四边形是正方形
C. 对角线互相垂直的四边形是菱形
D. 四个角相等的四边形是矩形
考点: 命题与定理.
分析: 根据矩形、菱形、正方形的判定与性质分别判断得出答案即可.
解答: 解:A、根据对角线相等的四边形也可能是矩形,故此选项错误;
B、根据对角线互相垂直平分的四边形是菱形,故此选项错误;
C、根据对角线互相垂直平分的四边形是菱形,故此选项错误;
D、根据四个角相等的四边形是矩形,是真命题,故此选项正确.
故选:D.
点评: 此题主要考查了命题与定理,熟练掌握矩形、菱形、正方形的判定与性质是解题关键.
8.(3分)(2013• 德州)下列函数中,当x>0时,y随x的增大而增大的是( )
A. y=﹣x+1 B. y=x2﹣1 C. y= D. y=﹣x2+1
考点: 二次函数的性质;一次函数的性质;反比例函数的性质.
分析: 根据二次函数、一次函数、反比例函数的增减性,结合自变量的取值范围,逐一判断.
解答: 解:A、y=﹣x+1,一次函数,k<0,故y随着x增大而减小,错误;
B、y=x2﹣1(x>0),故当图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧(x<0),y随着x的增大而减小,正确.
C、y=,k=1>0,在每个象限里,y随x的增大而减小,错误;
D、y=﹣x2+1(x>0),故当图象在对称轴右侧,y随着x的增大而减小;而在对称轴左侧(x<0),y随着x的增大而增大,错误;
故选B.
点评: 本题综合考查二次函数、一次函数、反比例函数的增减性(单调性),是一道难度中等的题目.
9.(3分)(2013• 德州)一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是( )
A. 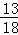 B.
B. 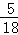 C. D.
C. D.
考点: 列表法与树状图法.
分析: 由在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,n次抛掷所出现的点数之和大于n2,则算过关;可得能过第二关的抛掷所出现的点数之和需要大于5,然后根据题意列出表格,由表格求得所有等可能的结果与能过第二关的情况,再利用概率公式求解即可求得答案.
解答: 解:∵在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,n次抛掷所出现的点数之和大于n2,则算过关;
∴能过第二关的抛掷所出现的点数之和需要大于5,
列表得:
6 7 8 9 10 11 12
5 6 7 8 9 10 11
4 5 6 7 8 9 10
3 4 5 6 7 8 9
2 3 4 5 6 7 8
1 2 3 4 5 6 7
1 2 3 4 5 6
∵共有36种等可能的结果,能过第二关的有26种情况,
∴能过第二关的概率是: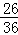 =
=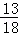 .
.
故选A.
点评: 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
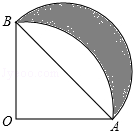
10.(3分)(2013• 德州)如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( )
A. 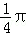 B.
B. 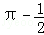 C. D.
C. D. 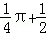
考点: 扇形面积的计算.
分析: 首先利用扇形公式计算出半圆的面积和扇形AOB的面积,然后求出△AOB的面积,用S半圆+S△AOB﹣S扇形AOB可求出阴影部分的面积.
解答: 解:在Rt△AOB中,AB=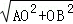 =
=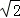 ,
,
S半圆=π×(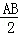 )2=π,
)2=π,
S△AOB=OB×OA=,
S扇形OBA=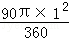 =
=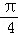 ,
,
故S阴影=S半圆+S△AOB﹣S扇形AOB=.
故选C.
点评: 本题考查了扇形的面积计算,解答本题的关键是熟练掌握扇形的面积公式,仔细观察图形,得出阴影部分面积的表达式.
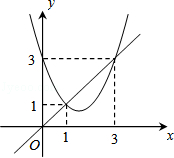
11.(3分)(2013• 德州)函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
考点: 二次函数图象与系数的关系.
分析: 由函数y=x2+bx+c与x轴无交点,可得b2﹣4c<0;当x=1时,y=1+b+c=1;当x=3时,y=9+3b+c=3;当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c<x,继而可求得答案.
解答: 解:∵函数y=x2+bx+c与x轴无交点,
∴b2﹣4c<0;
故①错误;
当x=1时,y=1+b+c=1,
故②错误;
∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
③正确;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故④正确.
故选B.
点评: 主要考查图象与二次函数系数之间的关系.此题难度适中,注意掌握数形结合思想的应用.
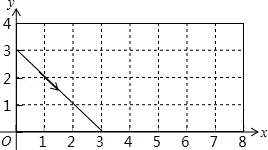
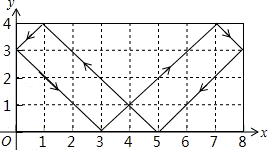
12.(3分)(2013• 德州)如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为( )
A. (1,4) B. (5,0) C. (6,4) D. (8,3)
考点: 规律型:点的坐标.
专题: 规律型.
分析: 根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2013除以6,根据商和余数的情况确定所对应的点的坐标即可.
解答: 解:如图,经过6次反弹后动点回到出发点(0,3),
∵2013÷6=335…3,
∴当点P第2013次碰到矩形的边时为第336个循环组的第3次反弹,
点P的坐标为(8,3).
故选D.
点评: 本题是对点的坐标的规律变化的考查了,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键,也是本题的难点.
二、填空题(共5小题,每小题4分,满分20分)
13.(4分)(2013• 德州)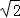 cos30°的值是
cos30°的值是 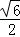 .
.
考点: 特殊角的三角函数值.
分析: 将特殊角的三角函数值代入计算即可.
解答: 解: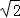 cos30°=
cos30°=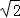 ×
×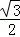 =
=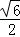 .
.
故答案为: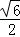 .
.
点评: 本题考查了特殊角的三角函数值,属于基础题,掌握几个特殊角的三角函数值是解题的关键.
14.(4分)(2013• 德州)如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因 两点之间线段最短 .

考点: 线段的性质:两点之间线段最短;三角形三边关系.
专题: 开放型.
分析: 根据线段的性质解答即可.
解答: 解:为抄近路践踏草坪原因是:两点之间线段最短.
故答案为:两点之间线段最短.
点评: 本题考查了线段的性质,是基础题,主要利用了两点之间线段最短.
15.(4分)(2013• 德州)甲乙两种水稻试验品中连续5年的平均单位面积产量如下(单位:吨/公顷)
品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
经计算,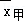 =10,
=10,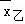 =10,试根据这组数据估计 甲 中水稻品种的产量比较稳定.
=10,试根据这组数据估计 甲 中水稻品种的产量比较稳定.
考点: 方差.
分析: 根据方差公式S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2]分别求出两种水稻的产量的方差,再进行比较即可.
解答: 解:甲种水稻产量的方差是:
[(9.8﹣10)2+(9.9﹣10)2+(10.1﹣10)2+(10﹣10)2+(10.2﹣10)2]=0.02,
乙种水稻产量的方差是:
[(9.4﹣10)2+(10.3﹣10)2+(10.8﹣10)2+(9.7﹣10)2+(9.8﹣10)2]=0.124.
∴0.02<0.124,
∴产量比较稳定的小麦品种是甲,
故答案为:甲
点评: 此题考查了方差,用到的知识点是方差和平均数的计算公式,一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
16.(4分)(2013• 德州)函数y=与y=x﹣2图象交点的横坐标分别为a,b,则+的值为 ﹣2 .
考点: 反比例函数与一次函数的交点问题.
专题: 计算题.
分析: 先根据反比例函数与一次函数的交点坐标满足两函数的解析式得到=x﹣2,去分母化为一元二次方程得到x2﹣2x﹣1=0,根据根与系数的关系得到a+b=2,ab=﹣1,
然后变形+得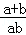 ,再利用整体思想计算即可.
,再利用整体思想计算即可.
解答: 解:根据题意得=x﹣2,
化为整式方程,整理得x2﹣2x﹣1=0,
∵函数y=与y=x﹣2图象交点的横坐标分别为a,b,
∴a、b为方程x2﹣2x﹣1=0的两根,
∴a+b=2,ab=﹣1,
∴+=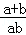 =
=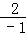 =﹣2.
=﹣2.
故答案为﹣2.
点评: 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了一元二次方程根与系数的关系.
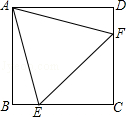
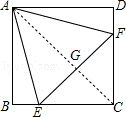
17.(4分)(2013• 德州)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:
①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+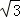 .
.
其中正确的序号是 ①②④ (把你认为正确的都填上).
考点: 正方形的性质;全等三角形的判定与性质;等边三角形的性质.
分析: 根据三角形的全等的知识可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正确,利用解三角形求正方形的面积等知识可以判断④的正误.
解答: 解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
∵在Rt△ABE和Rt△ADF中,
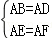 ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC﹣BE=CD﹣DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAD≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=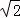 ,
,
设正方形的边长为a,
在Rt△ADF中,
a2+(a﹣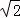 )2=4,
)2=4,
解得a=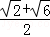 ,
,
则a2=2+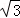 ,
,
S正方形ABCD=2+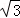 ,
,
④说法正确,
故答案为①②④.
点评: 本题主要考查正方形的性质的知识点,解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法,此题难度不大,但是有一点麻烦.
三、解答题(共7小题,满分64分)
18.(6分)(2013• 德州)先化简,再求值: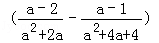 ÷
÷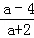 ,其中a=
,其中a=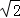 ﹣1.
﹣1.
考点: 分式的化简求值.
专题: 计算题.
分析: 将括号内的部分通分后相减,再将除法转化为乘法后代入求值.
解答: 解:原式=[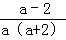 ﹣
﹣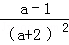 ]•
]•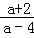
=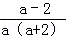 •
•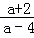
=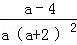 •
•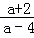
=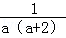 .
.
当a=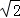 ﹣1时,原式=
﹣1时,原式=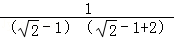 =1.
=1.
点评: 本题考查了分式的化简求值,熟悉通分、约分及因式分解是解题的关键.
19.(8分)(2013• 德州)某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
分组 划记 频数
2.0<x≤3.5 正正 11
3.5<x≤5.0  19
19
5.0<x≤6.5
6.5<x≤8.0
8.0<x≤9.5
合计  2
2
50
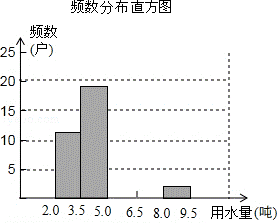
(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
考点: 频数(率)分布直方图;频数(率)分布表.
分析: (1)根据题中给出的50个数据,从中分别找出5.0<x≤6.5与 6.5<x≤8.0 的个数,进行划记,得到对应的频数,进而完成频数分布表和频数分布直方图;
(2)本题答案不唯一.例如:从直方图可以看出:①居民月平均用水量大部分在2.0至6.5之间;②居民月平均用水量在3.5<x≤5.0范围内的最多,有19户;
(3)由于50×60%=30,所以为了鼓励节约用水,要使60%的家庭收费不受影响,即要使30户的家庭收费不受影响,而11+19=30,故家庭月均用水量应该定为5吨.
解答: 解:(1)频数分布表如下:
分组 划记 频数
2.0<x≤3.5 正正 11
3.5<x≤5.0  19
19
5.0<x≤6.5
6.5<x≤8.0 
 13
13
5
8.0<x≤9.5
合计  2
2
50
频数分布直方图如下:
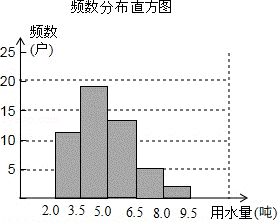
(2)从直方图可以看出:①居民月平均用水量大部分在2.0至6.5之间;②居民月平均用水量在3.5<x≤5.0范围内的最多,有19户;
(3)要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为5吨,因为月平均用水量不超过5吨的有30户,30÷50=60%.
点评: 本题考查读频数分布直方图和频数分布表的能力及利用统计图表获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
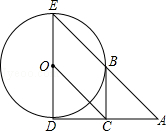
20.(8分)(2013• 德州)如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.
(1)求AD的长;
(2)BC是⊙O的切线吗?若是,给出证明;若不是,说明理由.
考点: 切线的判定与性质;直角三角形斜边上的中线;平行四边形的性质.
专题: 计算题.
分析: (1)连接BD,由ED为圆O的直径,利用直径所对的圆周角为直角得到∠DBE为直角,由BCOE为平行四边形,得到BC与OE平行,且BC=OE=1,在直角三角形ABD中,C为AD的中点,利用斜边上的中线等于斜边的一半求出AD的长即可;
(2)连接OB,由BC与OD平行,BC=OD,得到四边形BCDO为平行四边形,由AD为圆的切线,利用切线的性质得到OD垂直于AD,可得出四边形BCDO为矩形,利用矩形的性质得到OB垂直于BC,即可得出BC为圆O的切线.
解答: 解:(1)连接BD,则∠DBE=90°,
∵四边形BCOE为平行四边形,
∴BC∥OE,BC=OE=1,
在Rt△ABD中,C为AD的中点,
∴BC=AD=1,
则AD=2;
(2)连接OB,
∵BC∥OD,BC=OD,
∴四边形BCDO为平行四边形,
∵AD为圆O的切线,
∴OD⊥AD,
∴四边形BCDO为矩形,
∴OB⊥BC,
则BC为圆O的切线.
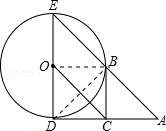
点评: 此题考查了切线的判定与性质,直角三角形斜边上的中线性质,以及平行四边形的判定与性质,熟练掌握切线的判定与性质是解本题的关键.
21.(10分)(2013• 德州)某地计划用120﹣180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式,并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石比原计划多5000米3,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万米3?
考点: 反比例函数的应用;分式方程的应用.
专题: 应用题.
分析: (1)利用“每天的工作量×天数=土方总量”可以得到两个变量之间的函数关系;
(2)根据“工期比原计划减少了24天”找到等量关系并列出方程求解即可;
解答: 解:(1)由题意得,y=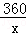
把y=120代入y=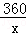 ,得x=3
,得x=3
把y=180代入y=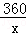 ,得x=2,
,得x=2,
∴自变量的取值范围为:2≤x≤3,
∴y=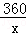 (2≤x≤3);
(2≤x≤3);
(2)设原计划平均每天运送土石方x万米3,则实际平均每天运送土石方(x+0.5)万米3,
根据题意得: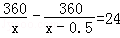
解得:x=2.5或x=﹣3
经检验x=2.5或x=﹣3均为原方程的根,但x=﹣3不符合题意,故舍去,
答:原计划每天运送2.5万米3,实际每天运送3万米3.
点评: 本题考查了反比例函数的应用及分式方程的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
22.(10分)(2013• 德州)设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
表1
1 | 2 | 3 | ﹣7 |
﹣2 | ﹣1 | 0 | 1 |
(2)数表A如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值
表2.
a | a2﹣1 | ﹣a | ﹣a2 |
2﹣a | 1﹣a2 | a﹣2 | a2 |
考点: 一元一次不等式组的应用.
分析: (1)根据某一行(或某一列)各数之和为负数,则改变改行(或该列)中所有数的符号,称为一次“操作”,先改变表1的第4列,再改变第2行即可;
(2)根据每一列所有数之和分别为2,0,﹣2,0,每一行所有数之和分别为﹣1,1,然后分别根据如果操作第三列或第一行,根据每行的各数之和与每列的各数之和均为非负整数,列出不等式组,求出不等式组的解集,即可得出答案.
解答: 解:(1)根据题意得:
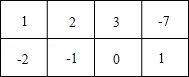 改变第4列
改变第4列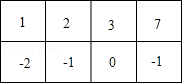 改变第2行
改变第2行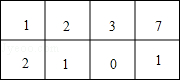
(2)∵每一列所有数之和分别为2,0,﹣2,0,每一行所有数之和分别为﹣1,1,
则①如果操作第三列,

则第一行之和为2a﹣1,第二行之和为5﹣2a,
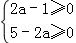 ,
,
解得:≤a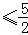 ,
,
又∵a为整数,
∴a=1或a=2,
②如果操作第一行,

则每一列之和分别为2﹣2a,2﹣2a2,2a﹣2,2a2,
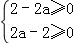 ,
,
解得a=1,
此时2﹣2a2,=0,2a2=2,
综上可知:a=1.
点评: 此题考查了一元一次不等式组的应用,关键是读懂题意,根据题目中的操作要求,列出不等式组,注意a为整数.
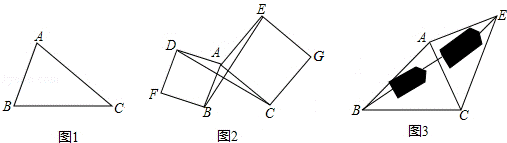
23.(10分)(2013• 德州)(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写做法,保留作图痕迹);
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.
考点: 四边形综合题.
专题: 计算题.
分析: (1)分别以A、B为圆心,AB长为半径画弧,两弧交于点D,连接AD,BD,同理连接AE,CE,如图所示,由三角形ABD与三角形ACE都是等边三角形,得到三对边相等,两个角相等,都为60度,利用等式的性质得到夹角相等,利用SAS得到三角形ABD与三角形ACE全等,利用全等三角形的对应边相等即可得证;
(2)BE=CD,理由与(1)同理;
(3)根据(1)、(2)的经验,过A作等腰直角三角形ABD,连接CD,由AB=AD=100,利用勾股定理求出BD的长,由题意得到三角形DBC为直角三角形,利用勾股定理求出CD的长,即为BE的长.
解答: 解:(1)完成图形,如图所示:
证明:∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,
∵在△CAD和△EAB中,
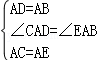 ,
,
∴△CAD≌△EAB(SAS),
∴BE=CD;
(2)BE=CD,理由同(1),
∵四边形ABFD和ACGE均为正方形,
∴AD=AB,AC=AE,∠BAD=∠CAE=90°,
∴∠CAD=∠EAB,
∵在△CAD和△EAB中,
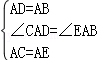 ,
,
∴△CAD≌△EAB(SAS),
∴BE=CD;
(3)由(1)、(2)的解题经验可知,过A作等腰直角三角形ABD,∠BAD=90°,
则AD=AB=100米,∠ABD=45°,
∴BD=100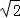 米,
米,
连接CD,则由(2)可得BE=CD,
∵∠ABC=45°,∴∠DBC=90°,
在Rt△DBC中,BC=100米,BD=100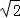 米,
米,
根据勾股定理得:CD=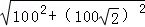 =100
=100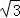 米,
米,
则BE=CD=100 米.
米.
点评: 此题考查了四边形综合题,涉及的知识有:全等三角形的判定与性质,等边三角形,等腰直角三角形,以及正方形的性质,勾股定理,熟练掌握全等三角形的判定与性质是解本题的关键.
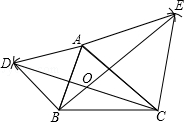
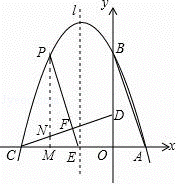
24.(12分)(2013• 德州)如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似点P的坐标;
②是否存在一点P,使△PCD得面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
考点: 二次函数综合题.
分析: (1)先求出A、B、C的坐标,再运用待定系数法就可以直接求出二次函数的解析式;
(2)①由(1)的解析式可以求出抛物线的对称轴,分类讨论当∠CEF=90°时,当∠CFE=90°时,根据相似三角形的性质就可以求出P点的坐标;
②先运用待定系数法求出直线CD的解析式,设PM与CD的交点为N,根据CD的解析式表示出点N的坐标,再根据S△PCD=S△PCN+S△PDN就可以表示出三角形PCD的面积,运用顶点式就可以求出结论.
解答: 解:(1)在Rt△AOB中,OA=1,tan∠BAO=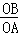 =3,
=3,
∴OB=3OA=3.
∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,
∴△DOC≌△AOB,
∴OC=OB=3,OD=OA=1,
∴A、B、C的坐标分别为(1,0),(0,3)(﹣3,0).
代入解析式为
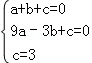 ,
,
解得: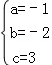 .
.
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)①∵抛物线的解析式为y=﹣x2﹣2x+3,
∴对称轴l=﹣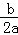 =﹣1,
=﹣1,
∴E点的坐标为(﹣1,0).
如图,当∠CEF=90°时,△CEF∽△COD.此时点P在对称轴上,即点P为抛物线的顶点,P(﹣1,4);
当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于点M,则△EFC∽△EMP.
∴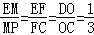 ,
,
∴MP=3EM.
∵P的横坐标为t,
∴P(t,﹣t2﹣2t+3).
∵P在二象限,
∴PM=﹣t2﹣2t+3,EM=﹣1﹣t,
∴﹣t2﹣2t+3=3(﹣1﹣t),
解得:t1=﹣2,t2=﹣3(与C重合,舍去),
∴t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3.
∴P(﹣2,3).
∴当△CEF与△COD相似时,P点的坐标为:(﹣1,4)或(﹣2,3);
②设直线CD的解析式为y=kx+b,由题意,得
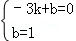 ,
,
解得: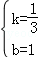 ,
,
∴直线CD的解析式为:y=x+1.
设PM与CD的交点为N,则点N的坐标为(t, t+1),
∴NM=t+1.
∴PN=PM﹣NM=t2﹣2t+3﹣(t+1)=﹣t2﹣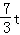 +2.
+2.
∵S△PCD=S△PCN+S△PDN,
∴S△PCD=PM•CM+PN•OM
=PN(CM+OM)
=PN•OC
=×3(﹣t2﹣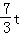 +2)
+2)
=﹣(t+)2+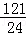 ,
,
∴当t=﹣时,S△PCD的最大值为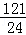 .
.
点评: 本题考查了相似三角形的判定及性质的运用,待定系数法求函数的解析式的运用,三角形的面积公式的运用,二次函数的顶点式的运用,解答本题时,先求出二次函数的解析式是关键,用函数关系式表示出△PCD的面积由顶点式求最大值是难点.


