(单词翻译:单击)
第一部分(选择题 共30分)
一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,满分24分)
1.(2013云南玉溪,1,3分)下列四个实数中,负数是( )
A.-2013 B.0 C.0.8 D.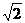
【答案】A
2.(2013云南玉溪,2,3分)如图是每个面上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面![]() 是( )
是( )
A.中 B. 钓 C.鱼 D.岛

【答案】C
3.(2013云南玉溪,3,3分)下列运算正确的是( )
A.x+y=xy B. 2x2-x2=1
C.2x·3x=6x D.x2 ÷x=x
【答案】D
4.(2013云南玉溪,4,3分)在下列图形中,既是轴对称图形又是中心对称图形的是( )

【答案】A
5.(2013云南玉溪,5,3分)一次函数y=x-2的图像不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
6.(2013云南玉溪,6,3分)若等腰三角形的两边长分别为4和8,则它的周长为( )
A.12 B.16 C.20 D.16或20
【答案】C
7.(2013云南玉溪![]() ,7,3分)如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点 O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
,7,3分)如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点 O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
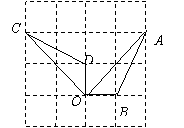

A.300 B.450 C.900 D.1350
【答案】C
8.(2013云南玉溪,8,3分)如图,在一块菱形菜地ABCD中,对角线AC与BD相交于点O,若在菱形菜地内均匀地撒上种子,则种子落在阴影部分的概率是( )
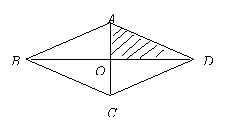

A.![]() 1 B.
1 B.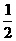 C.
C.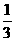 D.
D.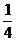
【答案】D
二、填空题(本![]() 大题共6小题,每小题3分,满分18分)
大题共6小题,每小题3分,满分18分)
9.(2013云南玉溪,9,3分)据统计,今年我市参加初中数学学业水平考试的学生人数约为27000人,把27000用科学计数法表示为___________.
【答案】2.7×104
10.(2013云南玉溪,10,3分)若数2,3,x,5,6五个数的平均数为4,则x的值为______ .
【答案】 4
11.(2013云南玉溪,11,3分)如图,AB∥CD,∠BAF=115°,则∠ECF的度数为 ______.
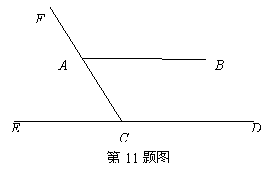

【答案】65°
12.(2013云南玉溪,12,3分)分解因式:ax2-ay2= ______.
【答案】 a(x+y)(x-y)
13.(2013云南玉溪,13,3分)若规定“*”的运算法则为:a*b=ab-1,则2*3= ______.
【答案】5
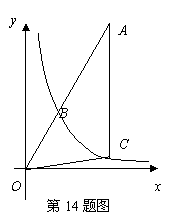
14.(2013云南玉溪,14,3分)反比例函数y=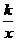 (x>0)的图像如图,点B在图像上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交y=
(x>0)的图像如图,点B在图像上,连接OB并延长到点A,使AB=2OB,过点A作AC∥y轴,交y=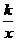 (x>0)的图像于点C,连接OC,S△AOC=5,则k=______.
(x>0)的图像于点C,连接OC,S△AOC=5,则k=______.

【答案】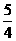
三、解答题(本大题共9小题,满分58分)
15.(2013云南玉溪,15,5分)计算:(-1)2-|-7|+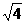 ×(2013-π)0+(
×(2013-π)0+(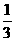 )-1
)-1
【答案】原式=1-7+2+3=-1.
16.(2013云南玉溪,16,5分)解不等式组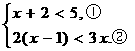
【答案】由①得x<3,由②得x> -2.∴![]() -2<x<3.
-2<x<3.
17.(2013云南玉溪,17,6分)如图,在□ABCD中,点E,F分别是边AD,BC的中点,求证:AF=CE.


【答案】证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵点E,F分别是边AD,BC的中点,
∴AE=CF.
∴四边形AECF是平行四边形.
∴AF=CE.
18.(2013云南玉溪,18,6分)端午节吃粽子是中华民族的传统习俗,据了解,甲厂家生产了A,B,C三个品种的盒装粽子,乙厂家生产D,E两个品种的盒装粽子![]() ,端午节前,某商场在甲乙两个厂家中各选购一个品种的盒装粽子销售.
,端午节前,某商场在甲乙两个厂家中各选购一个品种的盒装粽子销售.
(1)试用树状图或列表法写出所有选购方案;
(2)如果(1)中各种选购方案被选中的可能性相同,那么甲厂家的B品种粽子被选中的概率是多少?
【答案】(1)
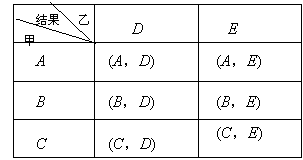

(2)P(B品种粽子被选中)=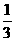 .
.
19.(2013云南玉溪,19,6分)为了解我市家庭月均用电量情况,有关部门随机抽查了我市1000户家庭的月均用电量,并将调查数据整理如下:
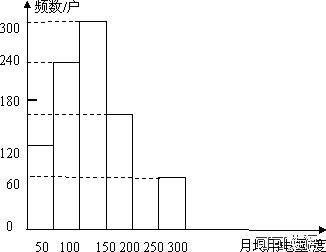
月均用电量a/度 | 频数/户 | 频率 |
0≤a<50 | 120 | 0.12 |
50≤a<100 | 240 | n |
100≤a<150 | 300 | 0.30 |
150≤a<200 | m | 0.16 |
200≤a<250 | 120 | 0.12 |
250≤a<300 | 60 | 0.06 |
合 计 | 1000 | 1 |
(1)频数分布表中的m= _________,n= _______;
(2)补全频数分布直方图;
(3)被调查的1000户家庭月均用电量的众数落在哪一个范围?
(4)求月均用电量小于150度的家庭数占被调查家庭总数的百分比.
【答案】(1)160 , ![]() 0.24;
0.24;
(2)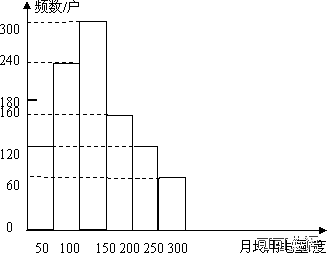
(3)被调查的1000户家庭月均用电量的众数落在100≤a<150范围内;
(4)月均用电量小于150度的家庭数占被调查家庭总数的百分比为: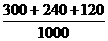 =66%.
=66%.
20.(2013云南玉溪,20,7分)在一个阳光明媚,微风习习的周末,小明和小强一起到聂耳文化广场放风筝,放了一会儿,两个人争吵起来:
小明说:“我的风筝飞得比你的高”.
小强说:“我的风筝引线比你的长,我的风筝飞得更高”.
谁的风筝飞得更高呢?于是他们将两个风筝引线的一段都固定在地面上的C处(如图),现已知小明的风筝引线(线段AC)长30米,小强的风筝引线(线段BC)长36米,在C处测得风筝A的仰角为600,风筝B的仰角为450,请通过计算说明谁的风筝飞得更高?
(结果精确到0.1米,参考数据: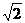 ≈1.41,
≈1.41,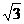 ≈1.73)
≈1.73)
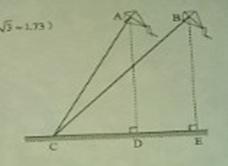
【答案】在Rt△ACD中,
∵sin∠ACD=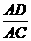 ,∴AD= AC·sin∠ACD=30×sin600=15
,∴AD= AC·sin∠ACD=30×sin600=15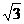 ≈26.0(米).
≈26.0(米).
在Rt△BCE中,
∵sin∠BCE=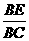 ,∴BE= BC·sin∠BCE=
,∴BE= BC·sin∠BCE=![]() 36×sin450=18
36×sin450=18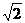 ≈25.5(米).
≈25.5(米).
∵26.0>25.5,
∴小明的风筝飞得更高.
21.(2013云南玉溪,21,7分)某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球.回校后,王老师和李老师编写了一道题:

同学们,请求出篮球和排球的单价各是多少元?
【答案】设排球的单价为x元,则篮球的单价为(x+30)元,根据题意,列方程得:
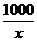 =
=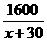 .
.
解之得x=50.
经检验,x=50是原方程的根.
当x=50时,x+30=80.
答:排球的单价为50元,则篮球的单价为80元.
22.(2013云南玉溪,22,7分)如图,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F,
(1)请探索OF![]() 和BC的关系并说明理由;
和BC的关系并说明理由;
(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.(结果保留π)
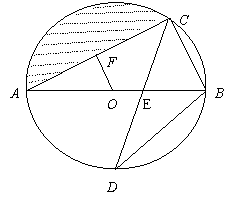
【答案】(1)OF∥BC,OF=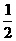 BC.
BC.
理由:由垂径定理得AF=CF.
∵AO=BO,∴OF是△ABC的中位线.
∴OF∥BC,OF=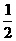 BC.
BC.
(2)连接OC.由(1)知OF=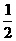 .
.
∵AB是⊙O的直径,∴∠ACB=90°.
∵∠D=30°,∴![]() ∠A=30°. ∴AB=2BC=2. ∴AC=
∠A=30°. ∴AB=2BC=2. ∴AC=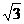 .
.
∴S△AOC=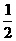 ×AC×OF=
×AC×OF=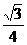 .
.
∵∠AOC=120°,OA=1,∴S扇形AOC=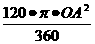 =
=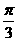 .
.
∴S阴影= S扇形AOC - S△AOC = 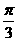 -
-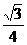 .
.
23.(2013云南玉溪,23,9分)如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式(关系式);
(2)求点A,B所在的直线的解析式(关系式);
(3)若动点P从点O出发,以每秒1个单位长度的速度沿着射线OM运动,设点P运动的时间为t秒,问:当t为何值时,四边形ABOP分别为平行四边形?等腰梯形?
(4)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t秒,连接PQ.问:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.


【答案】(1)把(1,0)代入y=a(x+2)2-4,得a=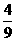 .
.
∴y=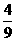 (x+2)2-4,即y=
(x+2)2-4,即y=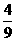 x2+
x2+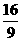 x-
x-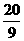 .
.
(2)设直线AB的解析式是y=kx+b.
∵点A(-2,-4),点B(1,0),
∴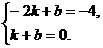 解得
解得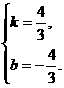
∴y=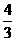 x—
x—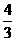 .
.
(3)由题意得OP=t,AB=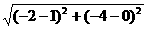 =5.
=5.
若四边形ABOP为平行四边形,则OP=AB=5,即当t=5时,四边形ABOP为平行四边形.
若四边形ABOP为等腰梯形,连接AP,过点P作PG⊥AB,过点O作OH⊥AB,垂足分别为G、H.易证△APG≌△BOH.
在Rt△OBM中,∵OM=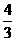 ,OB=1,∴BM=
,OB=1,∴BM=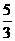 .∴OH=
.∴OH=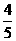 .∴BH=
.∴BH=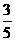 .
.
∴OP=GH=AB-2BH=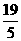 .
.
即当t=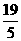 时,四边形ABOP为等腰梯形.
时,四边形ABOP为等腰梯形.

(4)将y=0代入y=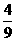 x2+
x2+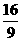 x-
x-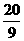 ,得
,得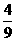 x2+
x2+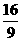 x-
x-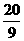 =0,解得x=1或-5.
=0,解得x=1或-5.
∴C(-5,0).∴OC=5.
∵OM∥AB, AD∥x轴,∴四边形![]() ABOD是平行四边形.
ABOD是平行四边形.
∴AD=OB=1.∴点D的坐标是(-3,-4).
∴S△DOC=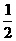 ×5×4=10.
×5×4=10.
过点P作PN⊥BC,垂足为N.易证△OPN∽△BOH.
∴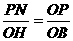 ,即
,即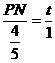 .∴PN=
.∴PN=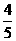 t.
t.
∴四边形CDPQ的面积S=S△DOC-S△OPQ=10-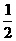 ×(5-2t )×
×(5-2t )×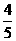 t=
t=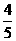 t2-2 t +10.
t2-2 t +10.
∴当t=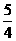 时,四边形CDPQ的面积S最小.
时,四边形CDPQ的面积S最小.
此时,点P的坐标是(-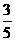 ,-1),点Q的坐标是(-
,-1),点Q的坐标是(-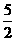 ,0),
,0),
∴PQ=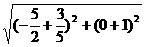 =
=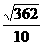 .
.


