(单词翻译:单击)
一.选择题:(每小题给出的四个选项中,只有一个正确选项,请将正确选项的标号填入题后的括号内.每小题3分,共24分)
1.(3分)(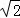 )0是( )
)0是( )
A. 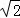 B. 1 C.
B. 1 C. 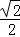 D. ﹣1
D. ﹣1
2.(3分)下列等式成立的是( )
A. |a|•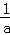 =1 B.
=1 B. 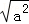 =a C.
=a C. 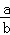 ÷
÷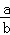 =
=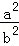 D. a﹣2a=﹣a
D. a﹣2a=﹣a
3.(3分)如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABCD与S四边形ECDF的大小关系是( )
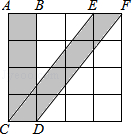
A. S四边形ABCD=S四边形ECDF B. S四边形ABCD<S四边形ECDF
C. S四边形ABCD=S四边形ECDF+1 D. S四边形ABCD=S四边形ECDF+2
4.(3分)如图所示,几何体的俯视图是( )
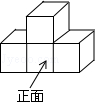
A.  B.
B.  C.
C.  D.
D. 
5.(3分)学校教学楼从每层楼到它上一层楼都要经过20级台阶,小明从一楼到五楼要经过的台阶数是( )
A. 100 B. 80 C. 50 D. 120
6.(3分)目前,我国大约有1.3亿高血压病患者,占15岁以上总![]() 人口数的10%﹣15%,预防高血压不容忽视.“千帕kpa”和“毫米汞柱mmHg”都是表示血压的单位,前者是法定的国际计量单位,而后者则是过去一直广泛使用的惯用单位.请你根据下表所提供的信息,判断下列各组换算正确的是( )
人口数的10%﹣15%,预防高血压不容忽视.“千帕kpa”和“毫米汞柱mmHg”都是表示血压的单位,前者是法定的国际计量单位,而后者则是过去一直广泛使用的惯用单位.请你根据下表所提供的信息,判断下列各组换算正确的是( )
千帕kpa | 10 | 12 | 16 | … |
毫米汞柱mmHg | 75 | 90 | 120 | … |
A. 13kpa=100mmHg B. 21kpa=150mmHg C. 8kpa=60mmHg D. 22kpa=160mmHg
7.(3分)从某校九年级中随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,5分.将测量的结果制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些学生分数的中位数是( )
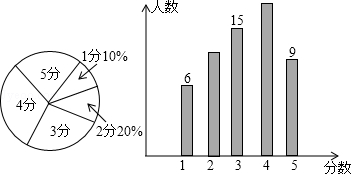
A. 1 B. 2 C. 3 D. 4
8.(3分)如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为(
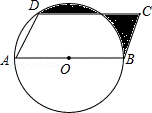
A. 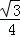 B.
B. 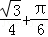 C.
C. 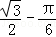 D.
D. 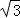
二、填空题(请把答案填在题中![]() 横线上,每小题3分,共计24分)
横线上,每小题3分,共计24分)
9.(3分)一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.496×108千米,以亿千米为单位表示这个数是 1.496 亿千米.
10.(3分)请你写出一个大于0而小![]() 于1的无理数
于1的无理数 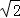 ﹣1 .
﹣1 .
11.(3分)一艘轮船顺水航行的速度是20海里/小时,逆水航行的速度是16海里/小时,则水流的速度是 2 海里/小时.
12.(3分)样本数据3,2,5,a,4的平均数是3,则a= 1 .
13.(3分)已知圆锥底面半径为5cm,高为12cm,则它的侧面展开图的面积是 65π cm2.
14.(3分)如图,矩形ABCD中,E是BC的中点,矩形ABCD的周长是20cm,AE=5cm,则AB的长为 4 cm.
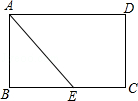
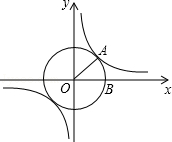
15.(3分)如图,在平面直角坐标系中,⊙O的半径为1,∠BOA=45°,则过A点的双曲线解析式是 y=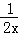 .
.
16.(3分)在等腰三角![]() 形中,马彪同学做了如下研究:已知一个角是60°,则另两个角是唯一确定的(60°,60°),已知一个角是90°,则另两个角
形中,马彪同学做了如下研究:已知一个角是60°,则另两个角是唯一确定的(60°,60°),已知一个角是90°,则另两个角![]() 也是唯一确定的(45°,45°),已知一个角是120°,则另两个角也是唯一确定的(30°,30°).由此马彪同学得出结论:在等腰三角形中,已知一个角的度数,则另两个角的度数也是唯一确定的.马彪同学的结论是 错误 的.(填“正确”或“错误”)
也是唯一确定的(45°,45°),已知一个角是120°,则另两个角也是唯一确定的(30°,30°).由此马彪同学得出结论:在等腰三角形中,已知一个角的度数,则另两个角的度数也是唯一确定的.马彪同学的结论是 错误 的.(填“正确”或“错误”)
三、解答题(解答时要写出必要的文字说明、证明过程或演算步骤,共9个题,满分102分)
17.(12分)
(1)计算:sin60°﹣|1﹣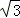 |+
|+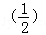 ﹣1
﹣1
(2)化简:(a+3)2﹣(a﹣3)2.
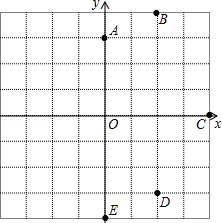
18.(10分)如图,在平面![]() 直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,﹣3),E(0,﹣4).写出D,C,B关于y轴对称点F,G,H的坐标,并画出F,G,H点.顺次而平滑地连接A,B,C,D,E,F,G,H,A各点.观察你画出的图形说明它具有怎样的性质,它象我们熟知的什么图形?
直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,﹣3),E(0,﹣4).写出D,C,B关于y轴对称点F,G,H的坐标,并画出F,G,H点.顺次而平滑地连接A,B,C,D,E,F,G,H,A各点.观察你画出的图形说明它具有怎样的性质,它象我们熟知的什么图形?
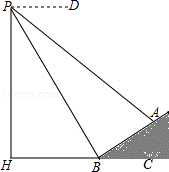
19.(10分)如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC=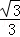 ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.
(1)求∠ABP的度数;
(2)求A,B两点间的距离.
20.(10分)甲、乙两位同学玩摸球游戏,准备了甲、乙两个口袋,其中甲口袋中放有标号为1,2,3,4,5的5个球,乙口袋中放有标号为1,2,3,4的4个球.游戏规则:甲从甲口袋摸一球,乙从乙口袋摸一球,摸出的两球所标数字之差(甲数字﹣乙数字)大于0时甲胜,小于0时乙胜,等于0时平局.你认为这个游戏规 则对双方公平吗?请说明理由.若不公平,请你对本游戏设计一个对双方都公平的游戏规则.
则对双方公平吗?请说明理由.若不公平,请你对本游戏设计一个对双方都公平的游戏规则.
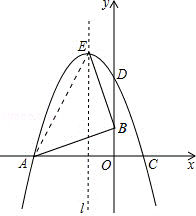
21.(10分)如图,直线L经过点A(0,﹣1),且与双曲线c:y=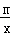 交于点B(2,1).
交于点B(2,1).
(1)求双曲线c及直线L的解析式;
(2)已知P(a﹣1,a)在双曲线c上,求P点的坐标.
22.(12分)某校家长委员会计划在九年级毕业生中实施“读万卷书,行万里路,了解赤峰,热爱家乡”主题活动,决定组织部分毕业生代表走遍赤峰全市12个旗、县、区考察我市创建文明城市成果,远航旅行社对学生实行九折优惠,吉祥旅行社对20人以内(含20人)学生旅行团不优惠,超过20人超出的部分每人按八折优惠.两家旅行社报价都是2000元/人.服务项目、旅行路线相同.请你帮助家长委员会策划一下怎样选择旅行社更省钱.
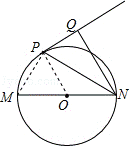
23.(12分)如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=3,NP=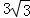 ,求NQ的长.
,求NQ的长.
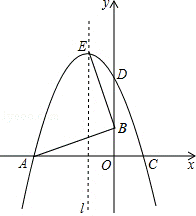
24.(12分)如图,已知△OAB的顶点A(﹣6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.
(1)写出C,D两点的坐标;
(2)求过A,D,C三点的抛物线的解析式,并求此抛物线顶点E的坐标;
(3)证明AB⊥BE.
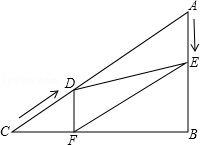
25.(14分)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
一.选择题:(每小题给出的四个选项中,只有一个正确选项,请将正确选项的标号填入题后的括号内.每小题3分,共24分)
1.B
2.D
3.A
4.C
5.B
6.C
7.C
8.A
二、填空题(请把答案填在题中![]() 横线上,每小题3分,共计24分)
横线上,每小题3分,共计24分)
9.1.496
10. 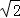 ﹣1
﹣1
11. 2
12. 1
13. 65π
14. 4
15. y=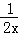
16.错误
三、解答题(解答时要写出必要的文字说明、证明过程或演算步骤,共9个题,满分102分)
17.解:(1)原式=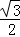 ﹣(
﹣(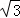 ﹣1)+2=
﹣1)+2=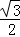 ﹣
﹣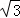 +1+2=﹣
+1+2=﹣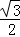 +3;
+3;
(2)原式=a2+6a+9﹣(a2﹣6a+9)=a2+6a+9﹣a2+6a﹣9=12a.
18.解:由题意得,F(﹣2,﹣3),G(﹣4,0),H(﹣2,4),
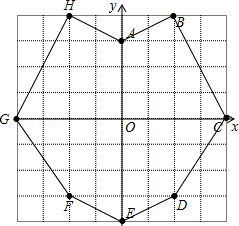
这个图形关于y轴对称,是我们熟知的轴对称图形.
19.解:(1)∵tan∠ABC=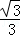 ,
,
∴∠ABC=30°;
∵从P点望山脚B处的俯角60°,
∴∠PBH=60°,
∴∠ABP=180°﹣30°﹣60°=90°
(2)由题意得:∠PBH=60°,
∵∠ABC=30°,
∴∠ABP=90°,又∠APB=30°,
∴△PAB为等腰直角三角形,
在直角△PHB中,PB=PH•tan∠PBH=300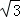 m.
m.
在直角△PBA中,AB=PB•tan∠BPC=300.
∴A、B两点之间的距离为300米.
20.解:游戏不公平,理由为:
列表得:
1 | 2 | 3 | 4 | 5 | |
1 | (1,1) | (2,1) | (3,1) | (4,1) | (5,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) | (5,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) | (5,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) | (5,4) |
所有等可能的情况有20种,其中摸出的两球所标数字之差(甲数字﹣乙数字)大于0的情况有10中,等于0的情况有4种,小于0的情况有6种,
则P甲获胜=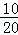 =
=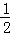 ,P乙获胜=
,P乙获胜=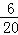 =
=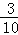 ,
,
∵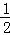 >
>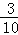 ,
,
∴游戏不公平;
若![]() 使游戏公平,修改规则为:中摸出的两球所标数字之和为偶数,甲获胜;之和为奇数,乙获胜.
使游戏公平,修改规则为:中摸出的两球所标数字之和为偶数,甲获胜;之和为奇数,乙获胜.
21.解:(1)将B(2,1)代入反比例解析式得:m=2,
则双曲线解析式为y=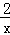 ,
,
设直线L解析式为y=kx+b![]() ,
,
将A与B坐标代入得: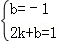 ,
,
解得: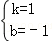 ,
,
则直线L解析式为y=x﹣1;
(2)将P(a﹣1,a)代入反比例解析式得:a(a﹣1)=2,
整理得:a2﹣a﹣2=0,即(a﹣2)(a+1)=0,
解得:a=2或a=﹣1,
则P坐标为(1,2)或(﹣2,﹣1).
22.解:设消费的钱数为y元,学生人数为x人,
则远航旅行社:y=0.9×2000x=1800x,
①若x≤20,则吉祥旅行社:y=2000x,
此时2000x>1800x,
选择远航旅行社更优惠;
②若x>20,则吉祥旅行社:y=2000×20+2000×0.8(x﹣20),
=40000+1600x﹣32000,
=1600x+8000,
当1600x+8000=18000x时,即x=40时,选择两个旅行社消费相同,
当x<40时,选择远航旅行社更优惠,
x>40时,选择吉祥旅行社更优惠,
综上所述,当学生人数少![]() 于40时,选择远航旅行社更优惠,
于40时,选择远航旅行社更优惠,
当学生人数等于40时,选择两家旅行社都一样,
当学生人数大于40时,选择吉祥旅行社更优惠.
23.(1)证明:连接OP.
∵直线PQ与⊙O相切于P点,
∴OP⊥PQ,
∵OP=ON,
∴∠OPN=∠ONP,
又∵NP平分∠MNQ,
∴∠OPN=∠PNQ,
∴OP∥NQ
∴NQ⊥PQ;
(2)解:连接MP.
∵MN是直径,
∴∠MPN=90°,
∴cos∠MNP=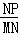 =
=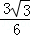 =
=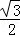 ,
,
∴∠MNP=30°,
∴∠PNQ=30°,
∴直角△PNQ中,NQ=NP•cos30°=3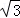 ×
×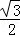 =
=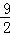 .
.
24.解:(1)∵将△OAB绕点O按顺时针旋转90°,得到△ODC,
∴△ODC≌△OAB,
∴OC=OB=2,OD=OA=6,
∴C(2,0),D(0,6);
(2)∵抛物线过点A(﹣6,0),C(2,0),
∴可设抛物线的解析式为y=a(x+6)(x﹣2)(a≠0),
∵D(0,6)在抛物线上,
∴6=﹣12a,
解得a=﹣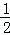 ,
,
∴抛物线的解析式为y=﹣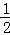 (x+6)(x﹣2),即y=﹣
(x+6)(x﹣2),即y=﹣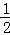 x2﹣2x+6,
x2﹣2x+6,
∵y=﹣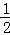 x2﹣2x+6=﹣
x2﹣2x+6=﹣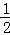 (x+2)2+8,
(x+2)2+8,
∴顶点E的坐标为(﹣2,8);
(3)连接AE.
∵A(﹣6,0),B(0,2),E(﹣2,8),
∴AB2=62+22=40,BE2=(﹣2﹣0)2+(8﹣2)2=40,AE2=(﹣2+6)2+(8﹣0)2=80,
∴AB2+BE2=AE2,
∴AB⊥BE.
25.解:(1)∵直角△ABC中,∠C=90°﹣∠A=30°.
∴AB=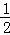 AC=
AC=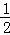 ×60=30cm.
×60=30cm.
∵CD=4t,AE=2t,
又∵在直角△CDF中,∠C=30°,
∴DF=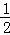 CD=2t,
CD=2t,
∴DF=AE;
(2)∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,即当t=10时,AEFD是菱形;
(3)△DEF为直角三角形,则一定有∠DEF=90°,DE∥BC,则AD=2AE,即60﹣4t=2×2t,解得:t=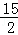 .
.


