(单词翻译:单击)
第Ⅰ卷 (选择题 共36分)
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均计零分.
1.下列计算,正确的是
A.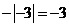 B.
B.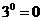 C.
C.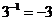 D.
D.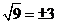
答案:A
解析:因为30=1,3-1=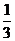 ,
,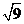 =3,所以,B、C、D都错,选A。
=3,所以,B、C、D都错,选A。
2.如图,AB//CD,∠CDE=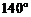 ,则∠A的度数为
,则∠A的度数为
A.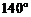 B.
B.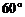
C.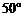 D.
D.
答案:D
解析:∠CDA=180°-140°=40°,由两直线平行,内错角相等,得:∠A=∠CDA=40°,选D。
3.估计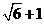 的值在
的值在
A. 2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
答案:B
解析:因为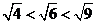 ,即2<
,即2<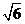 <3,所以,3<
<3,所以,3<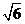 +1<4,选B。
+1<4,选B。
4.化简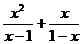 的结果是
的结果是
A.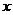 +1 B.
+1 B.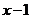
C.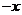 D.
D.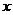
答案:D
解析:原式=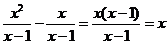 ,故选D。
,故选D。
5.某种商品每件的标价是330元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为
A.240元 B.250元
C.280元 D.300元
答案:A
解析:设进价为x元,则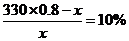 ,解得:x=240,故选A>
,解得:x=240,故选A>
6.如图,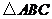 中,AB=AC=10,BC=8,AD平分
中,AB=AC=10,BC=8,AD平分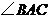 交
交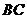 于点
于点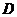 ,点
,点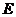 为
为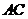 的中点,连接
的中点,连接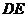 ,则
,则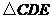 的周长为
的周长为
A.20 B.18
C.14 D.13
答案:C
解析:因为AB=AC,AD平分∠BAC,所以,D为BC中点,又E为AC中点,所以,DE=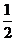 AB=5,DC=4,EC=5,故所求周长为5+5+4=14。
AB=5,DC=4,EC=5,故所求周长为5+5+4=14。
7.若关于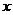 的一元二次方程
的一元二次方程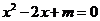 有两个不相等的实数根,则
有两个不相等的实数根,则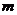 的取
的取
值范围是
A. 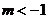 B.
B.  C.
C. 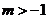 D.
D. 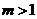
答案:B
解析:△=4-4m>0,解得:m<1,选B。
8. 对于非零实数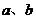 ,规定
,规定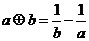 ,若
,若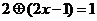 ,则
,则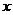 的值为
的值为
A.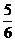 B.
B.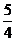 C.
C.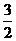 D.
D.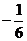
答案:A
解析:依题意,有: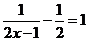 ,解得:x=
,解得:x=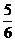
9.图(1)是一个长为2 a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是
A. ab B.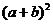
C.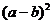 D. a2-b2
D. a2-b2
答案:C
解析:大正方形面积为:(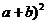 ,矩形面积为:4ab,所以,中间空的部分的面积为:
,矩形面积为:4ab,所以,中间空的部分的面积为: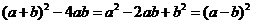 ,选C。
,选C。
10.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是
A.90° B.60°
C.45° D.30°
答案:D
解析:当OP与圆O相切时,∠OAP取得最大值,此时OP⊥AP,OP=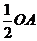 ,
,
∠OAP=30°,选D>
11. 将抛物线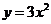 向左平移2个单位,再向下平移1个单位,所得抛物线为( )
向左平移2个单位,再向下平移1个单位,所得抛物线为( )
A. 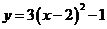 B.
B.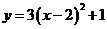
C. 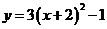 D.
D.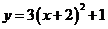
答案:C
解析:抛物线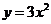 向左平移2个单位得到
向左平移2个单位得到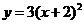 ,再向下平移1个单位,得:
,再向下平移1个单位,得: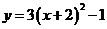
12.如图,在边长为2的正方形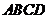 中,
中,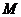 为边
为边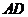 的中点,延长
的中点,延长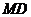 至点
至点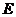 ,使
,使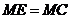 ,以
,以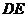 为边作正方形
为边作正方形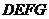 ,点
,点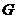 在边
在边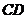 上,则
上,则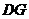 的长为
的长为
A.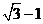 B.
B.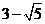
C.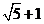 D.
D.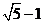
答案:D
解析:ME=MC=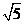 ,MD=1,所以,DG=DE=
,MD=1,所以,DG=DE=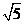 -1,选D。
-1,选D。
第Ⅱ卷 (非选择题 共84分)
 14.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号是 .
14.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号是 .
答案:②
解析:中心对称图形就是图形绕着对称中心旋转180度后与原来的图形完全重合,在②处涂黑,刚好可以做到。
15. 从1、2、3、4中任取一个数作为十位上的数字,再从2、3、4中任取一个数作为个位上的数字,那么组成的两位数是3的倍数的概率是 .
答案: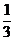
解析:共有12个数字,其中3的倍数有:12、24、33、42,共4个,故所求的概率为: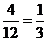
16.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
答案:24
解析:这个零件的表面积与原正方体的表面积相同,为4×6=24。
17. 已知正比例函数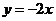 与反比例函数
与反比例函数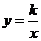 的图象的一个交点坐标为(-1,2),则另一个交点的坐标为 .
的图象的一个交点坐标为(-1,2),则另一个交点的坐标为 .
答案: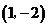
解析:反比例函数的图象关于原点对称,点(-1,2)关于原点对称的点为(1,-2),故填(1,-2)。
18.已知矩形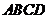 中,
中,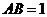 ,在
,在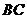 上取一点
上取一点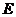 ,沿
,沿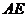 将
将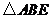 向上折叠,使
向上折叠,使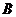 点落在
点落在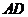 上的
上的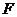 点.若四边形
点.若四边形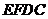 与矩形
与矩形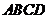 相似,则
相似,则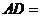 .
.
答案: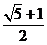
解析:
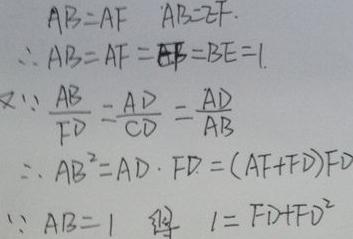
(FD+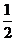 )2=
)2=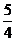 ,得FD=
,得FD=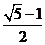 ,又AD=AD+FD,AF=1
,又AD=AD+FD,AF=1
AD=1+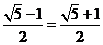
三、解答题:本大题共7小题,满分60分.解答时,要写出必要的文字说明、证明过程或演算步骤.
19.(本题满分8分)
先化简,再求值:
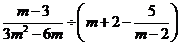 ,其中
,其中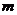 是方程
是方程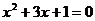 的根.
的根.
解析:
解:原式=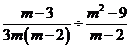
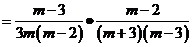
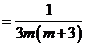 .
.
∵m是方程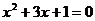 的根,∴
的根,∴ 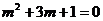 .
.
∴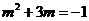 ,即
,即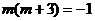 .
.
∴原式=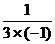 =
=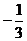 .
.
20.(本题满分8分)
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点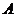 和点
和点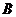 在小正方形的顶点上.
在小正方形的顶点上.
(1)在图1中画出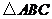 ,使
,使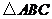 为直角三角形(点
为直角三角形(点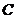 在小正方形的顶点上,画出一个即可);
在小正方形的顶点上,画出一个即可);
(2)在图2中画出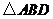 ,使
,使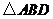 为等腰三角形(点
为等腰三角形(点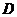 在小正方形的顶点上,画出一个即可).
在小正方形的顶点上,画出一个即可).
解析:
20.(本题满分8分)
(1)正确画图(参考图1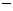 图4)
图4)
(2)正确画图(参考图5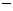 图8)
图8)
21.(本题满分8分)
“六·一”前夕,质检部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品.以下是根据抽查结果绘制出的不完整的统计表和扇形图:
请根据上述统计表和扇形图提供的信息,完成下列问题:
(1)补全上述统计表和扇形图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?
解析:
21.(本题满分8分)
解:(1)
(每空1分) ………………………………………………4分
(2)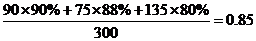 .
.
答:从该超市这三类儿童用品中随机购买一件买到合格品的概率是0.85
22.(本题满分8分)
交通安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点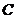 ,再在笔直的车道上确定点
,再在笔直的车道上确定点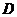 ,使
,使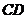 与垂直,测得
与垂直,测得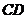 的长等于21米,在上点
的长等于21米,在上点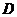 的同侧取点
的同侧取点 、
、 ,使
,使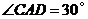 ,
,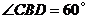 .
.
(1)求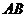 的长(精确到0.1米,参考数据:
的长(精确到0.1米,参考数据: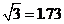 ,
,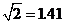 );
);
(2)已知本路段对汽车限速为40千米/小时,若测得某辆汽车从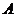 到
到 用时为2秒,这辆汽车是否超速?说明理由.
用时为2秒,这辆汽车是否超速?说明理由.
解析:
22.(本题满分8分)
解:(1)在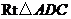 中,CD=21,
中,CD=21,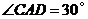 ,
,
∴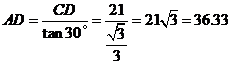 ;……………………………2分
;……………………………2分
在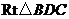 中,CD=21,
中,CD=21,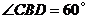 ,
,
∴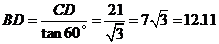 . …………………………4分
. …………………………4分
所以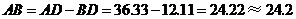 (米).…………5分
(米).…………5分
(2)汽车从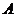 到
到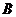 用时2秒,所以速度为
用时2秒,所以速度为
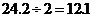 (米/秒).
(米/秒).
又因为 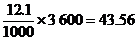 .
.
所以该汽车速度为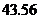 千米/小时,大于40千米/小时,
千米/小时,大于40千米/小时,
故此汽车在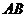 路段超速. ……………………………………………………8分
路段超速. ……………………………………………………8分
23.(本题满分8分)
如图,在平面直角坐标中,直角梯形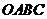 的边
的边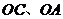 分别在
分别在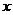 轴、
轴、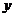 轴上,
轴上,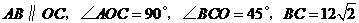 ,点
,点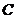 的坐标为
的坐标为
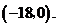
(1)求点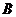 的坐标;
的坐标;
(2)若直线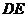 交梯形对角线
交梯形对角线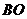 于点
于点 ,交
,交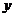 轴于点
轴于点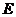 ,且
,且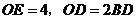 ,求直线
,求直线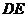 的解析式.
的解析式.
解析:
23.(本题满分8分)
解:(1)过点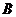 作
作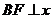 轴于
轴于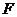 .在
.在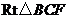 中,∠BCO=45°,BC=
中,∠BCO=45°,BC=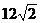 ,
,
∴ CF=BF=12. …………………1分
∵点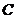 的坐标为
的坐标为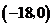 ,
,
∴AB=OF=18-12=6.
∴点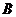 的坐标为
的坐标为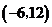 .
.
(2)过点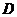 作
作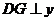 轴于点
轴于点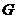 .
.
∵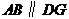 ,∴
,∴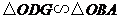 .
.
∴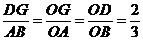 .
.
∵AB=6,OA=12,∴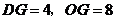 .
.
∴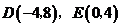 .
.
设直线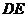 的解析式为
的解析式为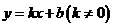 ,将
,将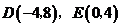 代入,得
代入,得
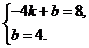 解之,得
解之,得 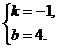
∴直线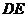 解析式为
解析式为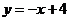 .
.
24.(本题满分10分)
如图,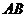 是⊙O的直径,
是⊙O的直径,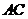 是弦,直线
是弦,直线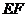 经过点
经过点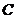 ,
,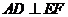 于点
于点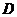 ,
,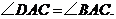
(1)求证: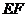 是⊙O的切线;
是⊙O的切线;
(2)求证: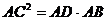 ;
;
(3)若⊙O的半径为2,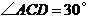 ,求图中阴影部
,求图中阴影部
解析:
(1)证明:连接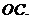
∵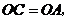 ∴
∴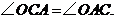
∵∠DAC=∠BAC,∴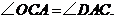
∴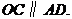 …………………………1分
…………………………1分
又∵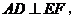 ∴
∴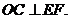
∴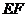 是⊙O的切线. ……………………3分
是⊙O的切线. ……………………3分
(2)证明:连接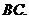
∵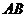 是⊙O的直径,∴
是⊙O的直径,∴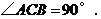
∴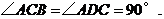
又∵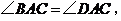
∴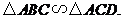
∴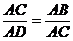 , 即
, 即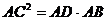 . ……………6分
. ……………6分
(3)解:∵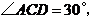 ∴
∴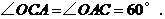
∴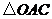 是等边三角形.
是等边三角形.
∴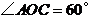 ,
,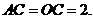
在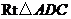 中,AC=2,∠ACD=30°,
中,AC=2,∠ACD=30°,
∴AD=1,CD=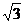 . …………………………………………………………8分
. …………………………………………………………8分
∴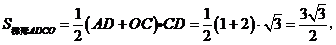
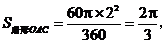
∴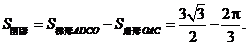 ………………………………10分
………………………………10分
25. (本题满分10分)
如图,在平面直角坐标系中,二次函数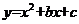 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点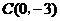 ,点P是直线BC下方抛物线上的一个动点.
,点P是直线BC下方抛物线上的一个动点.
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形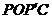 .是否存在点P,使四边形
.是否存在点P,使四边形 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大
解析:
解:(1)将B、C两点的坐标代入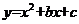 ,得
,得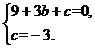
解之,得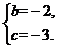
所以二次函数的解析式为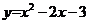 . ………………………………… 3分
. ………………………………… 3分
(2)如图1,假设抛物线上存在点P,使四边形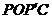 为菱形,连接
为菱形,连接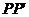 交CO于点E.
交CO于点E.
∵四边形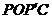 为菱形,
为菱形,
∴PC=PO,且PE⊥CO.
∴OE=EC=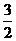 ,即P点的纵坐标为
,即P点的纵坐标为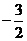 .……5分
.……5分
由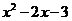 =
=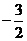 ,得
,得
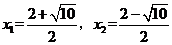 (不合题意,舍去)
(不合题意,舍去)
所以存在这样的点,此时P点的坐标为(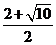 ,
,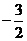 ). …………7分
). …………7分
(3)如图2,连接PO,作PM⊥x于M,PN⊥y于N.设P点坐标为(x,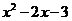 ),
),
由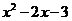 =0,得点A坐标为(-1,0).
=0,得点A坐标为(-1,0).
∴AO=1,OC=3, OB=3,PM=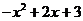 ,PN=x.
,PN=x.
∴S四边形ABPC=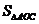 +
+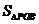 +
+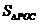
=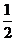 AO·OC+
AO·OC+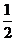 OB·PM+
OB·PM+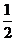 OC·PN
OC·PN
=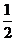 ×1×3+
×1×3+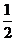 ×3×(
×3×(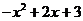 )+
)+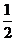 ×3×x
×3×x
=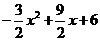
=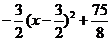 . ………………………8分
. ………………………8分
易知,当x=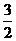 时,四边形ABPC的面积最大.此时P点坐标为(
时,四边形ABPC的面积最大.此时P点坐标为(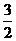 ,
,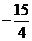 ),四边形ABPC的最大面积为
),四边形ABPC的最大面积为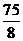 . ………………………………………………………………10分
. ………………………………………………………………10分


