(单词翻译:单击)
一、选择题(本题有10小题,每小题4分,共40分)
1. 计算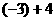 的结果是
的结果是
A. -7 B. -1 C. 1 D. 7
2. 右图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一个组是
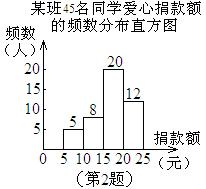
A. 5~10元 B. 10~15元 C. 15~20元 D. 20~25元
3. 如图所示的支架是由两个长方体构成的组合体,则它的主视图是

4. 要使分式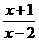 有意义,则
有意义,则 的取值应满足
的取值应满足
A.  B.
B. 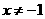 C.
C. 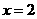 D.
D. 
5. 计算 的结果是
的结果是
A.  B.
B.  C.
C.  D.
D. 
6. 小明记录了一星期每天的最高气温如下表,则这个星期每天最高气温的中位数是
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
最高气温(℃) | 22 | 24 | 23 | 25 | 24 | 22 | 21 |
A. 22℃ B. 23℃ C. 24℃ D. 25℃
7. 一次函数 的图像与
的图像与 轴交点的坐标是
轴交点的坐标是
A. (0,-4) B. (0,4) C. (2,0) D. (-2,0)
8. 如图,已知点A,B,C在⊙O上, 为优弧,下列选项中与∠AOB相等的是
为优弧,下列选项中与∠AOB相等的是
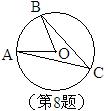
A. 2∠C B. 4∠B C. 4∠A D. ∠B+∠C
9. 20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵,设男生有 人,女生有
人,女生有 人,根据题意,列方程组正确的是
人,根据题意,列方程组正确的是
A.  B.
B. 
C. 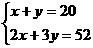 D.
D. 
10. 如图,矩形ABCD的顶点A在第一象限,AB∥ 轴,AD∥
轴,AD∥ 轴,且对角线的交点与原点重合,在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数
轴,且对角线的交点与原点重合,在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数 中,
中, 的值的变化情况是
的值的变化情况是

A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
二、填空题(本题有6小题,每小题5分,共30分)
11. 因式分解:
因式分解: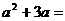 _________
_________
12. 如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=_________度
13. 不等式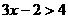 的解是_________
的解是_________
14. 如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是_________
15. 请举反例说明“对于任意实数 ,
,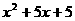 的值总是正数”是假命题,你举的反例是
的值总是正数”是假命题,你举的反例是 = _________(写出一个
= _________(写出一个 的值即可)
的值即可)
16. 如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE= AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相较于另一点F,且EG:E
AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相较于另一点F,且EG:E F=
F= 。当边AD或BC所在的直线与⊙O相切时,AB的长是_________
。当边AD或BC所在的直线与⊙O相切时,AB的长是_________
三、解答题(本题有8小题,共80分)
17.(本题10分)
(1)计算:
(2)化简:
18.(本题8分)

如图,在所给 方格纸中,每个小正方形边长都是1,标号为①,②,③的三个三角形均为格点三角形(顶点在方格顶点处)。请按要求将图甲、图乙中的指定图形分割成三个三角形,使它们与标号为①,②,③的三个三角形分别对应全等。
方格纸中,每个小正方形边长都是1,标号为①,②,③的三个三角形均为格点三角形(顶点在方格顶点处)。请按要求将图甲、图乙中的指定图形分割成三个三角形,使它们与标号为①,②,③的三个三角形分别对应全等。
(1)图甲中的格点正方形ABCD;
(2)图乙中的平行四边形ABCD。
注:图甲、图乙在答题卡上,分割线画成实线。
19.(本题8分)
一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球、8个黑球、7 个红球。
个红球。
(1)求从袋中摸出一个球是黄球的 概率;
概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是 ,求从袋中取出黑球的个数。
,求从袋中取出黑球的个数。
20.(本题10分)
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且 DE∥AB,过点E作EF⊥DE,交BC的延长线于点F。
DE∥AB,过点E作EF⊥DE,交BC的延长线于点F。

(1)求∠F的度数;
(2)若CD=2,求DF的长。
21.(本题10分)
如图,抛物线
 与
与 轴交于A,B两点,它们的对称轴与
轴交于A,B两点,它们的对称轴与 轴交于点N,过顶点M作ME⊥
轴交于点N,过顶点M作ME⊥ 轴于点E,连结BE交MN于点F。已知点A的坐标为(-1,0)
轴于点E,连结BE交MN于点F。已知点A的坐标为(-1,0)
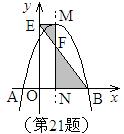
(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比。
22.(本题8分)
勾股定理神秘而美妙, 它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感。他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明。下面是小聪利用图1证明勾股定理的过程:
它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感。他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明。下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠ DAB=90°,求证:
DAB=90°,求证: 。
。
证明:连结DB,过点D作BC边上的高DF,
则DF=EC= ,
,
∵  ,
,

又∵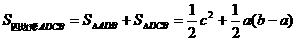 ,
,
∴  ,
,
∴ 
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°。

求证: 。
。
证明:连结_________
∵  _________
_________
又∵  _________
_________
∴ _________
∴  。
。
23.(本题12分)
八(1)班五位同学参加学校举办的数学竞赛,试卷中共有20道题,规定 每题答对得5分,答错扣2分,未答得0分。赛后A,B, C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表:
每题答对得5分,答错扣2分,未答得0分。赛后A,B, C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表:
参赛同学 | 答对题数 | 答错题数 | 未答题数 |
| 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知:A,B,C,D,E五位同学成绩分别是95分,81分,64分,83 分,58分。
分,58分。
①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况。请指出哪位同学记错了,并写出他的 实际答题情况(直接写出答案即可)。
实际答题情况(直接写出答案即可)。
24.(本题14 分)
分)
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿 轴正方
轴正方 向以每秒1个单位的速度运动,同时动点
向以每秒1个单位的速度运动,同时动点 C从点B出发,沿射线BO方向以每秒2个单位的速度运动。以CP,CO为邻边构造□PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为
C从点B出发,沿射线BO方向以每秒2个单位的速度运动。以CP,CO为邻边构造□PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为 秒。
秒。
(1)当点 C运动到线段OB的中点时,求
C运动到线段OB的中点时,求 的值及点E的坐标;
的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;

(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在第一、四象限,在运动过程中,设□PCOD的面积为S。
①当点M,N中,有一点落在四边形ADEC的边上时,求出所有满足条件的 的值;
的值;
②若点M,N中恰好只有一个点落在四边形ADEC内部(不包括边界)时,直接写出S的取值范围。





 A
A
