(单词翻译:单击)
A卷(共120分)
第Ⅰ卷(选择题 共48分)
一、选择题:(共12个小题,每小题4分,共48分)在每小题给出的四个选项中只有一项是正确的,把正确的字母填涂在答题卡上相应的位置。
1.在实数 、
、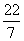 、0,
、0, 、
、 、
、 中,有理数有
中,有理数有
A.1个 B.2个 C.3个 D.4个
2. 下列图形中,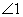 与
与 是对顶角的是
是对顶角的是


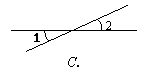
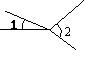

3.下列计算正确的是
A. B.
B. C.
C. D.
D.
4.某班数学学习小组某次测验成绩分别是63、72、49、66、81、53、92、69,则这组数据的极差为
A.47 B.43 C.34 D.29
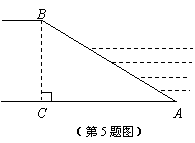
5.拦水坝横断面如图所示,迎水坡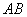 的坡比是
的坡比是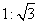 ,拔高
,拔高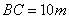 ,则坡面
,则坡面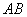 的长度是
的长度是
A.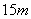 B.
B.
C. D.
D.
6.凉山州的人口约有473万人,将473万人用科学记数法表示应为
A. 人 B.
人 B.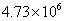 人 C.
人 C. 人 D.
人 D. 人
人
7.如果两个相似多边形面积的比为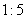 ,则它们的相似比为
,则它们的相似比为
A.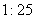 B.
B.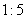 C.
C. D.
D.
8.分式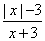 的值为零,则
的值为零,则 的值为
的值为
A.3 B.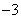 C.
C. D.任意实数
D.任意实数
9.下列图形中阴影部分的面积相等的是
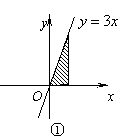




A.② ③ B.③ ④ C.① ② D.① ④
10.在 中,若
中,若 ,则
,则 的度数是
的度数是
A. B.
B.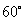 C.
C.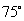 D.
D.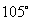
11.函数 与
与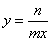 ,其中
,其中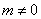 ,
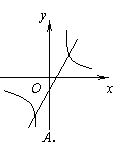
,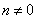 ,那么它们在同一坐标系中的图象可能是
,那么它们在同一坐标系中的图象可能是




12.已知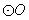 的直径
的直径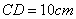 ,
,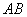 是
是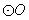 的弦,
的弦, ,且
,且 ,垂足为
,垂足为 ,则
,则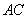 的长为
的长为
A.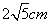 B.
B. C.
C. 或
或 D.
D. 或
或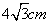
第Ⅱ卷(选择题 共72分)
注意事项:
1.答卷前将密封线内的项目填写清楚,准考证号前七位填在密封线内,末两位填在卷首方框内。
2.答题时用蓝黑色墨水钢笔或黑色签字笔直接答在试卷上。


二、填空题:(共5小题,每小题4分,共20分)
13.函数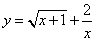 中,自变量
中,自变量 的取值范围是_______________。
的取值范围是_______________。
14.顺次连接矩形四边中点所形成的四边形是_______________,学校的一块菱形花圃两对角线的长分别是 和
和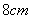 ,则这个花圃的面积为_______________。
,则这个花圃的面积为_______________。
15.已知 ,
, ,则
,则 _______________ 。
_______________ 。
16.已知直角三角形两边的长分别是3和4,则第三边的长为 _______________。
17.“服务社会,提升自我。”凉山州某学校积极开展志愿者服务活动,来自九年级的5名同学(三男二女)成立了“交通秩序维护”小分队,若从该小分队中任选两名同学进行交通秩序维护,则恰好是一男一女的概率是_______________。


三、解答题:(共2小题,每小题6分,共12分)
18.计算: ;
;
19.先化简,再求值: ,其中
,其中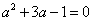 ;
;


四、解答题:(共3小题,每小题8分,共24分)
20.州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)。


请根据图中提供的信息,回答下列问题:
(1) _______ %,并写出该扇形所对圆心角的度数为_______,请补全条形图。
_______ %,并写出该扇形所对圆心角的度数为_______,请补全条形图。
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
21.如图,分别以 的直角边
的直角边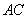 及斜边
及斜边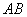 向外作等边
向外作等边 及等边
及等边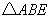 ,已知:
,已知: ,
,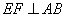 ,垂足为
,垂足为 ,连接
,连接 。
。
(1)是说明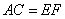 ; (2)求证:四边形
; (2)求证:四边形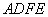 是平行四边形。
是平行四边形。

22.实验与探究:
三角点阵中前 行的点数计算
行的点数计算
下图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……,第 行有
行有 个点……
个点……
 ……
……
容易发现,10是三角点阵中前4行的点数之和。你能发现300是前多少行的点数之和吗?
如果用实验的方法,由上而下地逐行相加其点数,虽然你能发现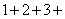 …
…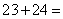 300,得知300是前24行的点数之和,但是这样寻找答案需要花费较多时间,能否更简捷地得出结果呢?
300,得知300是前24行的点数之和,但是这样寻找答案需要花费较多时间,能否更简捷地得出结果呢?
我们先探究三角点阵中前 行的点数和与
行的点数和与 的数量关系。
的数量关系。
前 行的点数和是
行的点数和是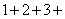 …
…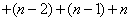 ,可以发现,
,可以发现,

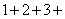 …
…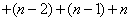
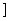
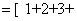 …
…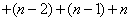
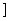 +
+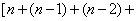 …
…
把两个中括号中的第一项相加,第二项相加……第 项相加,上式等号的后边变形为这
项相加,上式等号的后边变形为这 个小括号都等于
个小括号都等于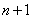 ,整个式子等于
,整个式子等于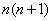 ,于是得到
,于是得到
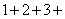 …
…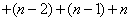
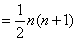
这就是说,三角点阵中前 行的点数的和是
行的点数的和是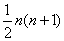 。
。
下面用一元二次方程解决上述问题:
设三角点阵中前 行的点数和为300,则有
行的点数和为300,则有 ,
,
整理这个方程,得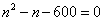 ,
,
解方程得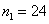 ,
, 。
。
根据问题中未知数的意义确定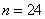 ,即三角点阵中前
,即三角点阵中前 项的和是300.
项的和是300.
请你根据上述材料回答下列问题:
(1)三角点阵中前 行的点数和能是600吗?如果能,求出
行的点数和能是600吗?如果能,求出 ;如果不能,试用一元二次方程说明道理;
;如果不能,试用一元二次方程说明道理;
(2)如果把图中的三角点阵中各行的点数依次换为2、4、6、……、 ,你能探究出前
,你能探究出前 行的点数之和满足什么规律吗?这个三角点阵中前
行的点数之和满足什么规律吗?这个三角点阵中前 行的点数之和能是600吗?如果能,求出
行的点数之和能是600吗?如果能,求出 ;如果不能,试用一元二次方程说明道理。
;如果不能,试用一元二次方程说明道理。


五、解答题:(共2小题,每小题8分,共16分)
23.如图所示,正方形网格中, 为格点三角形(即三角形的顶点都在格点上)。
为格点三角形(即三角形的顶点都在格点上)。

(1)把 沿
沿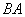 方向平移后,点
方向平移后,点 移到点
移到点 ,在网格中画出平移后得到的
,在网格中画出平移后得到的 ;
;
(2)把 绕点
绕点 按逆时针旋转
按逆时针旋转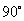 ,在网格中画出旋转后的
,在网格中画出旋转后的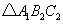 ;
;
(3)如果网格中小正方形的白南昌为1,求点 经过(1)、(2)变换的路径总长。
经过(1)、(2)变换的路径总长。
24.我州某校计划购买甲、乙两种树苗共1000株用以绿化校园。甲种树苗每株25元,乙种树苗每株30元,通过调查了解,甲、乙两种树苗的成活率分别是90%和95%。
(1)若购买这两种树苗共用去28000元,则甲、乙两种树苗各购买多少株?
(2)要使这批树苗的成活率不低于92%,则甲种树苗最多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用。
B卷(共30分)


六、填空题:(共2小题,每小题5分,共10分)
25.关于 的方程
的方程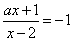 的解是正数,则
的解是正数,则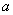 的取值范围是______________。
的取值范围是______________。
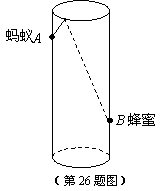
26.如图,圆柱形容器高 ,底面周长为
,底面周长为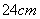 ,在杯内壁离杯底
,在杯内壁离杯底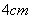 的点
的点 处有一滴蜂蜜,此时已知蚂蚁正好在杯外壁,离杯上沿
处有一滴蜂蜜,此时已知蚂蚁正好在杯外壁,离杯上沿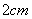 与与密封相对的
与与密封相对的 处,则蚂蚁从外壁
处,则蚂蚁从外壁 处到达内壁
处到达内壁 处的最短距离为______________
处的最短距离为______________ 。
。


七、解答题:(共2小题,27题8分,28题12分,共20分)
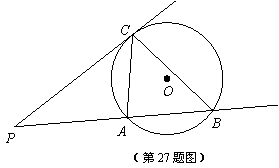
27.已知:如图,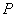 是
是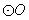 外一点,过点
外一点,过点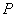 引圆的切线
引圆的切线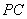 (
(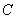 为切点)和割线
为切点)和割线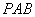 ,分别交
,分别交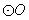 于
于 、
、 ,连接
,连接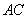 、
、 。
。
(1)求证: ;
;
(2)利用(1)的结论,已知 ,
, ,求
,求 的长。
的长。
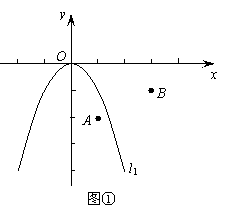
28.如图①,在平面直角坐标系中,点 的坐标为(
的坐标为( ,
, ),点
),点 (3,
(3,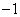 ),二次函数
),二次函数 的图象为
的图象为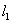 。
。
(1)平移抛物线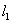 ,使平移后的抛物线经过点
,使平移后的抛物线经过点 ,但不经过点
,但不经过点 。
。
①满足此条件的函数解析式有_______________个;
②写出向下平移且过点 的解析式_______________。
的解析式_______________。
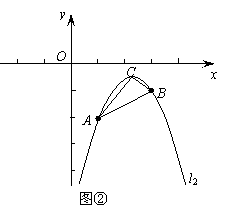
(2)平移抛物线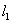 ,使平移后的抛物线经过
,使平移后的抛物线经过 、
、 两点,所得的抛物线为
两点,所得的抛物线为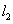 ,如图②,求抛物线
,如图②,求抛物线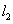 的解析式及顶点坐标,并求
的解析式及顶点坐标,并求 的面积;
的面积;
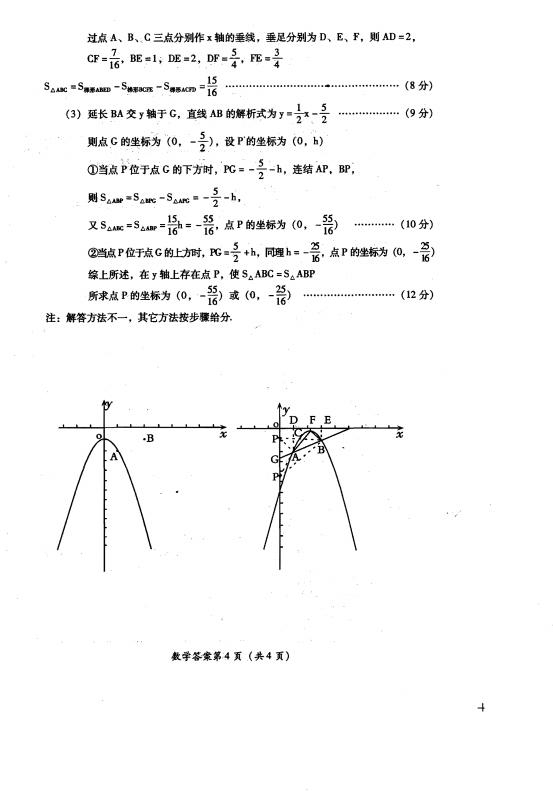
(3)在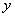 轴上是否存在点
轴上是否存在点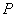 ,使
,使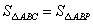 ,若存在,求出点
,若存在,求出点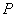 的坐标;若不存在,请说明好理由。
的坐标;若不存在,请说明好理由。