(单词翻译:单击)
一、选择题(本部分共12小题,每小题2分,共24分)
1. -2的相反数是
A. 2 B.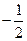 C.
C. 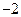 D.
D.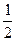
2.某校七年级有5名同学参加射击比赛,成绩分别为7,8,9,10,8(单位:环)。则这5名同学成绩的众数是
A.7 B.8 C. 9 D. 10
3.下列各式计算正确的是
A.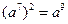 B.
B.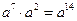 C.
C.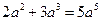 D.
D.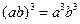
4.左下图为某几何体的示意图,则该几何体的主视图应为
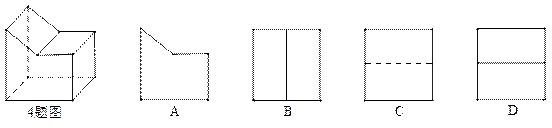
5.第六次全国人口普查数据显示:泸州市常住人口大约有4220000人,这个数用科学记数法表示正确的是
A.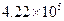 B.
B. 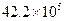 C.
C. 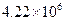 D.
D. 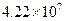
6.四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是
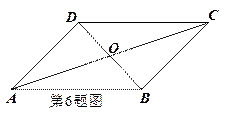
A.AB//DC,AD//BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB//DC,AD=BC
7.函数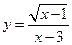 自变量
自变量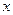 取值范围是
取值范围是
A.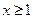 且
且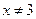 B.
B.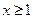 C.
C.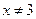 D.
D. 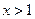 且
且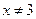
8.若关于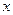 的一元二次方程
的一元二次方程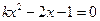 有两个不相等的实数根,则实数
有两个不相等的实数根,则实数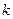 的取值范围是
的取值范围是
A.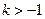 B.
B.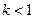 且
且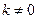 C.
C. 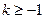 且
且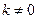 D.
D. 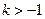 且
且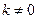
9.已知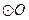 的直径CD=10cm,AB是
的直径CD=10cm,AB是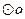 的弦,
的弦,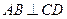 ,垂足为M,且AB=8cm,则AC的长为
,垂足为M,且AB=8cm,则AC的长为
A.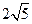
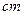 B.
B. 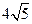
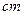 C.
C. 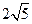
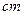 或
或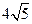
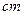 D.
D. 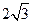
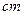 或
或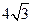
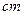
10.设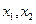 是方程
是方程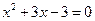 的两个实数根,则
的两个实数根,则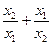 的值为
的值为
A.5 B.-5 C.1 D.-1
11.如图,点E是矩形ABCD的边CD上一点,把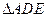 沿AE对折,点D的对称点F恰好落在BC一,已知折痕
沿AE对折,点D的对称点F恰好落在BC一,已知折痕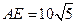
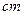 ,且
,且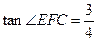 ,那么该矩形的周长为
,那么该矩形的周长为
A.72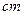 B. 36
B. 36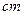 C. 20
C. 20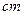 D. 16
D. 16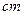
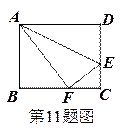
12.如图,在等腰直角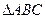 中,
中,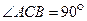 ,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且
,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且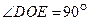 ,DE交OC于点P.则下列结论:
,DE交OC于点P.则下列结论:
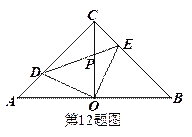
(1)图形中全等的三角形只有两对;
(2)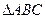 的面积等于四边形CDOE面积的2倍;
的面积等于四边形CDOE面积的2倍;
(3)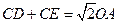 ;
;
(4)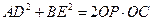 .其中正确的结论有
.其中正确的结论有
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共4小题,每小题4分,共16分.)
13.分解因式: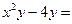 .
.
14.在一只不透明的口袋中放入红球6个,黑球2个,黄球n个。这些球除颜色不同外,其它无任何差别,搅匀后随机从中摸出一个恰好是黄球的概率为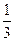 ,则放入口袋中的黄球总数n= .
,则放入口袋中的黄球总数n= .
15.如图,从半径为9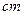 的圆形纸片上剪去
的圆形纸片上剪去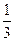 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 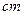 .
.

16. 如图,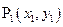 ,
,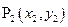 ,……
,……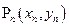 在函数
在函数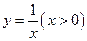 的图像上,
的图像上,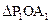 ,
,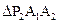 ,
,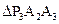 ,……
,……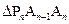 都是等腰直角三角形,斜边
都是等腰直角三角形,斜边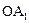 、
、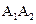 、
、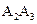 ,……
,……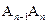 都在
都在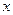 轴上(n是大于或等于2的正整数),则点
轴上(n是大于或等于2的正整数),则点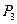 的坐标是 ;点
的坐标是 ;点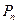 的坐标是 (用含n的式子表示).
的坐标是 (用含n的式子表示).
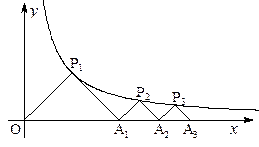
三、(本大题共3个小题,每小题6分,共18分)
17.计算: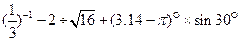 .
.
18.先化简: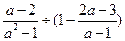 ,再求值,其中
,再求值,其中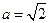 .
.
19.如图,已知□ABCD中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.求证:AB=BE.
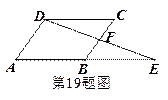
四、(本大题共2个小题,每小题7分,共14分)
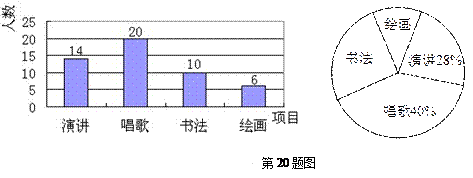
20.某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛。它们分别是演讲、唱歌、书法、绘画。要求每位同学必须参加,且限报一项活动。以以九年级(1)班为样本进行统计,并将统计结果绘成如下两幅统计图。请你结合下图所给出的信息解答下列问题:
(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
21.某中学为提升学生的课外阅读能力,拓展学生的知识面,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个。已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本。
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
五、(本大题共2个小题,每小题8分,共16分)
22.如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为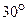 ,在A、C之间选择一点B (A、B、C三点在同一直线上),用测角仪测得塔顶D的仰角为
,在A、C之间选择一点B (A、B、C三点在同一直线上),用测角仪测得塔顶D的仰角为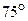 ,且AB间距离为40
,且AB间距离为40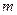 .
.
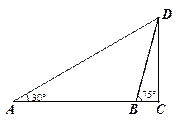
(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示)。
23.如图,已知函数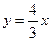 与反比例函数
与反比例函数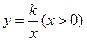 的图象交于点A.将
的图象交于点A.将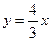 的图象向下平移6个单位后与双曲线
的图象向下平移6个单位后与双曲线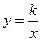 交于点B,与
交于点B,与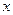 轴交于点C.
轴交于点C.
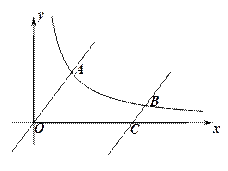
(1)求点C的坐标;
(2)若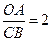 ,求反比例函数的解析式.
,求反比例函数的解析式.
24.如图,D为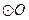 上一点,点C在直径BA的延长线上,且
上一点,点C在直径BA的延长线上,且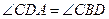 .
.
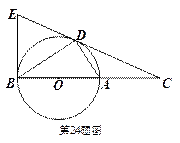
(1)求证: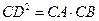 ;
;
(2)求证: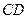 是
是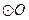 的切线;
的切线;
(3)过点B作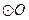 的切线交CD的延长线于点E,若BC=12,
的切线交CD的延长线于点E,若BC=12,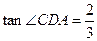 ,求BE的长.
,求BE的长.
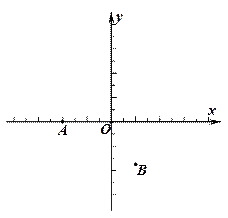
25.如图,在直角坐标系中,点A的坐标为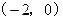 ,点B的坐标为
,点B的坐标为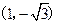 ,已知抛物线
,已知抛物线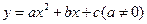 经过三点A、B、O(O为原点).
经过三点A、B、O(O为原点).
(1)求抛物线的解析式;
(2)在该抛物线的对称轴上,是否存在点C,使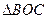 的周长最小。若存在,求出点C的坐标。若不存在,请说明理由;
的周长最小。若存在,求出点C的坐标。若不存在,请说明理由;
(3)如果点P是该抛物线上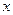 轴上方的一个动点,那么
轴上方的一个动点,那么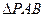 是否有最大面积。若有,求出此时P点的坐标及
是否有最大面积。若有,求出此时P点的坐标及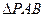 的最大面积;若没有,请说明理由。(注意:本题中的结果均保留根号)。
的最大面积;若没有,请说明理由。(注意:本题中的结果均保留根号)。