(单词翻译:单击)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确的,请用2B铅笔把答题卡上相应的选项标号涂黑)
1.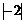 的值等于 ( ▲ )
的值等于 ( ▲ )
A.2 B.-2 C.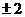 D.
D.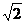
答案:A
解析:负数的绝对值是它的相反数,所以|-2|=2,选A。
2.函数y=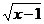 +3中自变量
+3中自变量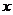 的取值范围是 ( ▲ )
的取值范围是 ( ▲ )
A.x>1B.x ≥1C.x≤1 D.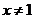
答案:B
解析:由二次根式的意义,得:x-1≥0,所以,x≥1,选B。
3.方程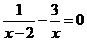 的解为( ▲ )
的解为( ▲ )
A.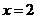 B.
B.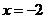 C.
C.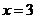 D.
D.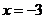
答案:C
解析:去分母,得:x-3(x-2)=0,即x-3x+6=0,解得:x=3,经检验x=3是原方程的解,选C。
4.已知一组数据:15,13,15,16,17,16,14,15,则这组数据的极差与众数分别是( ▲ )
A.4,15 B.3,15 C.4,16 D.3,16
答案:A
解析:极差为:17-13=4;数据15出现的次数最多,故众数为15,选A。
5.下列说法中正确的是 ( ▲ )
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
答案:D
解析:A、B都漏掉关键词“平行”,应该是“两条平行直线”,故错;两平行直线被第三条直线所截得的同位角的平分线互相平行,不垂直,故C错;由两直线平行,同旁内角互补,及角平分线的性质,可得D是正确的。
6.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是 ()
A.30cm2 B.30πcm2C.15cm2 D.15πcm2
答案:B
解析:圆柱侧面展开图为长方形,长为圆柱的底面圆周长:6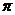 ,因此,侧面积为S=6
,因此,侧面积为S=6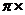 5=30πcm2
5=30πcm2
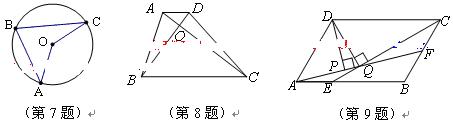
7.如图,A、B、C是⊙O上的三点,且∠ABC=70°,则∠AOC的度数是 ()
A.35°B.140° C.70°D.70°或140°
答案:B
解析:同弧所对圆周角是它所对圆周角的一半,所以,∠AOC=2∠ABC=140°,选B。
8.如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,AD=1,BC=4,则△AOD与△BOC的面积比等于()
A.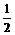 B.
B.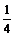 C.
C.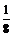 D.
D.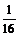
答案:D
解析:由AD∥BC,得△AOD∽△COB,相似三角形的面积比等于相似比的平方,所以,△AOD与△COB的面积比为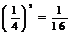 ,选D。
,选D。
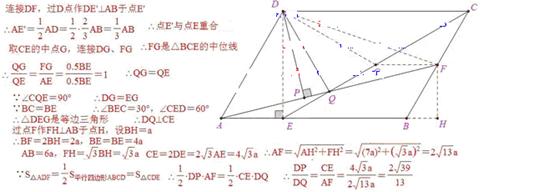
9.如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于 ()
A.3∶4B.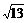 ∶
∶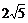 C.
C.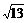 ∶
∶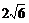 D.
D.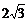 ∶
∶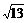
答案:D
解析:
10.已知点A(0,0),B(0,4),C(3,t+4),D(3,t). 记N(t)为□ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为()
A.6、7B.7、8C.6、7、8 D.6、8、9
答案:C
解析:当t=0时,▱ABCD的四个项点是A(0,0),B(0,4),C(3,4),D(3,0),
符合条件的点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),共6个,N(t)=6,故选项B不正确.
当t=1时,▱ABCD的四个项点是A(0,0),B(0,4),C(3,5),D(3,1),
同理知N(t)=7,故选项D不正确.
当t=2时,▱ABCD的四个项点是A(0,0),B(0,4),C(3,6),D(3,2),
同理知N(t)=8,故选项A不正确.
故选C.
二、填空题(本大题共8小题,每小题2分,共16分. 不需写出解答过程,只需把答案直接填写在答题卡上相应的位置)
11.分解因式:2x2-4x=.
答案:2x(x-2)
解析:原式有公因式2x,直接提公因式即可,故原式=2 x(x-2)
12.去年,中央财政安排资金8 200 000 000元,免除城市义务教育学生学杂费,支持进城务工人员随迁子女公平接受义务教育,这个数据用科学记数法可表示为 元.
答案:8.2×109
解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
8 200 000 000=8.2×109
13.已知双曲线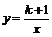 经过点(-1,2),那么k的值等于 .
经过点(-1,2),那么k的值等于 .
答案:-3
解析:净点(-1,2)代入双曲线,得:2=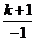 ,解得:k=-3
,解得:k=-3
14.六边形的外角和等于 °.
答案:360
解析:n边形的内角和为(n-2)×180°,将n=6代入,得:360°
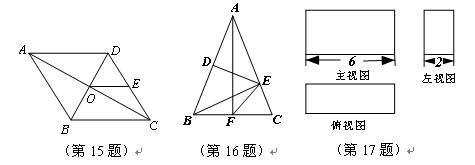
15.如图,菱形ABCD中,对角线AC交BD于O,AB=8, E是CD的中点,则OE的长等于 .
答案:4
解析:菱形的对角线互相平分,所以,O为BD中点,又E为CD中点,所以,OE为三角DBC的中位线,OE=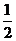 BC=4
BC=4
16.如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC= °.
答案:45
解析:因为DE垂直平分AB,且BE⊥AC,所以,DA=DB=DE,所以,∠ABE=45°,
又因为AB=AC,AF⊥BC,所以,∠C=∠ABC,设∠C的度数为x°,
由直角三角形斜边上的中线等于斜边的一半,得FE=FC=FB,所以,∠FEC=x°,
∠FEB=∠FBE=x°-45°,因此,在三角形EBC中,有:x+x-45=90,得:x=67.5°,
∠EFC=180°=67.5°-67.5°=45°。
17.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是.
答案:72
解析:由三视图可知,这个几何体是长方体,底面积为:6×2=12,因为体积为36,所以,长方体的高为3,表面积为:2×6×2+2×3×2+2×6×3=72。
18.已知点D与点A(8,0),B(0,6),C(a,-a)是一平行四边形的四个顶点,则CD长的最小值为.
答案:7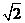
解析:∵OA=8,OB=6 ∴AB=10
(1) 当CD是平行四边形的边时,CD=AB=10
(2)当CD是平行四边形的对角线时,
CD过AB的中点P(4,3),过点P作PH⊥直线y=-x于点H,则PC=PH时最短,此时CD=2PH最小,过B、A分别作直线y=-x的垂线,可求得CD=2PH=7.
三、解答题
19.(本题满分8分)计算:
(1)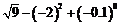 ; (2)(x+1)2-(x+2)(x-2).
; (2)(x+1)2-(x+2)(x-2).
解析:

20.(本题满分8分)
(1)解方程:x2+3x-2=0; (2)解不等式组: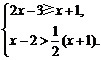
解析:
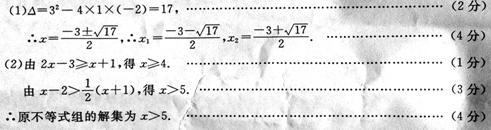
21.(本题满分6分)如图,在Rt△ABC中,∠C=90°,AB=10,sin∠A=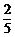 ,求BC的长和tan∠B的值.
,求BC的长和tan∠B的值.
解析:
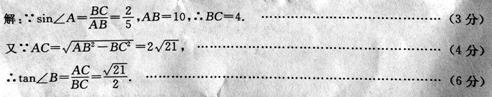
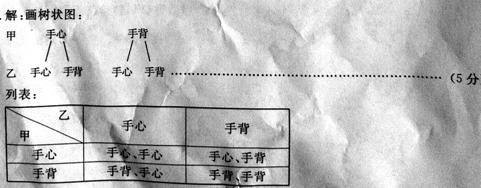
22.(本题满分8分)小明与甲、乙两人一起玩“手心手背”的游戏.他们约定:如果三人中仅有一人出“手心”或“手背”,则这个人获胜;如果三人都出“手心”或“手背”,则不分胜负,那么在一个回合中,如果小明出“手心”,则他获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
解析:

23.(本题满分6分)某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查.下面是根据收集的数据绘制的两幅不完整的统计图.

请根据图中提供的信息,解答下面的问题:
(1)此次共调查了▲名学生,户型统计图中“艺术鉴赏”部分的圆心角是▲度.
(2)请把这个条形统计图补充完整.
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
解析:

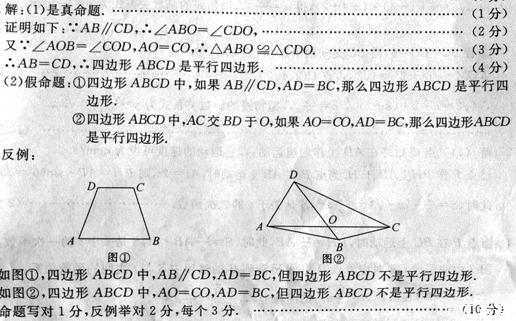
24.(本题满分10分)如图,四边形ABCD中,对角线AC与BD相交于O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”为结论构成命题.
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例;
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么….”的形式)
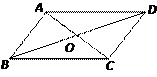
解析:
25.(本题满分8分)已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
A元素含量 | 单价(万元/吨) | |
甲原料 | 5% | 2.5 |
乙原料 | 8% | 6 |
已知用甲原料提取每千克A元素要排放废气1吨,用乙原料提取每千克A元素要排放废气0.5吨.若某厂要提取A元素20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
解析:

26.(本题满分10分)如图,直线x=-4与x轴交于E,一开口向上的抛物线过原点O交线段OE于A,交直线x=-4于B.过B且平行于x轴的直线与抛物线交于C,直线OC交直线AB于D,且AD:BD=1:3.
(1)求点A的坐标;
(2)若△OBC是等腰三角形,求此抛物线的函数关系式.

解析:

 27.(本题满分10分)如图1,菱形ABCD中,∠A=600.点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止;点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t s.△APQ的面积s(cm2)与t(s)之间函数关系的图像由图2中的曲线段OE与线段EF、FG给出.
27.(本题满分10分)如图1,菱形ABCD中,∠A=600.点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止;点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t s.△APQ的面积s(cm2)与t(s)之间函数关系的图像由图2中的曲线段OE与线段EF、FG给出.

(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
解析:

28.(本题满分10分)下面给出的正多边形的边长都是20 cm.请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明.
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.
解析: