(单词翻译:单击)
第Ⅰ卷(选择题 共42分)
一、选择题(本大题共14小题,每小题3分,共42分)在 每小题所给出的四个选项中,只有一项是符合题目要求的.
每小题所给出的四个选项中,只有一项是符合题目要求的.
1.-3的相反数是
(A)3. (B)-3. (C)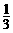 . (D)
. (D)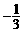 .
.
2.根据世界贸易组织(W T O  )秘书处初步统计数据,2013年中国货物进出口总额为4 160 000 000 000美元,超过美国成为世界第一货物贸易大国.将这个数据用科学记数法可以记为
)秘书处初步统计数据,2013年中国货物进出口总额为4 160 000 000 000美元,超过美国成为世界第一货物贸易大国.将这个数据用科学记数法可以记为
(A)
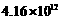 美元. (B)
美元. (B)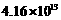 美元.
美元.
(C)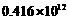 美元. (D)
美元. (D)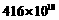 美元.
美元.
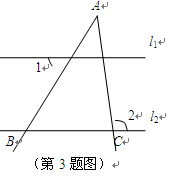
3.如图,已知 l1∥l2,∠A=40°,∠1=60°,则∠2的度数为
l1∥l2,∠A=40°,∠1=60°,则∠2的度数为
4.下列计算正确的是
(A)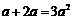 . (B)
. (B)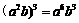 .
.
(C)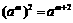 . (D)
. (D)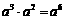 .
.
5.不等式组-2≤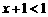 的解集,在数轴上表示正确的是
的解集,在数轴上表示正确的是
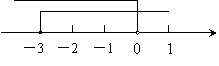
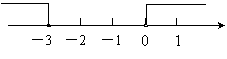
(A) (B)
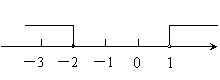
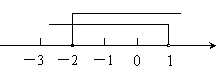
(C) (D)
6.当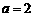 时,
时,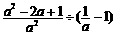 的结果是
的结果是
(A)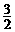 . (B)
. (B)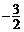 .
.
(C)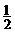 . (D)
. (D)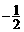 .
.
7.将一个n边形变成n+1边形,内角和将
(A)减少180°. (B)增加90°.
(C)增加180°. (D)增加360°.
8.某校为了丰富学生的校园生活,准备购买一批陶笛,已知A型陶笛比B型陶笛的单价低20元,用2700元购买A型陶笛与用4500 元购买B型陶笛的数量相同
元购买B型陶笛的数量相同 ,设A型陶笛的单价为
,设A型陶笛的单价为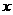 元,依题意,下面所列方程正确的是
元,依题意,下面所列方程正确的是
(A)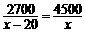 . (B)
. (B)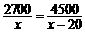 .
.
(C)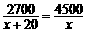 . (D)
. (D)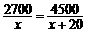 .
.
9.如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为
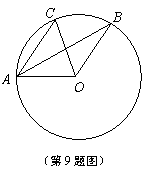
(A)25°.
(B)50°.
(C)60°.
(D)80°.
10.从1,2,3,4中任取两个不同的数,其乘积大于4的概率是
(A)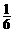 . (B)
. (B)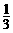 .(C)
.(C)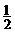 .(D)
.(D)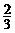 .
.
11.一个几何体的三视图如图所示,这个几何体的侧面积为
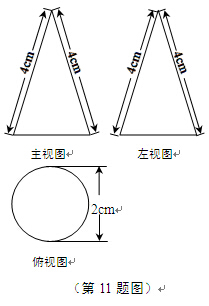
(A)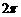 cm2.
cm2. 
(B)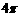 cm2.
cm2.
(C)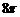 cm2.
cm2.
(D)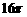 cm2.
cm2.
12.请你计算:
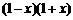 ,
,
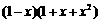 ,
,
猜想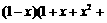 …
…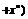 的结果是
的结果是
(A)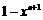 . (B)
. (B)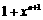 .
.
(C)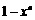 . (D)
. (D)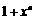 .
.
13.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时 后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为____________.
后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为____________.
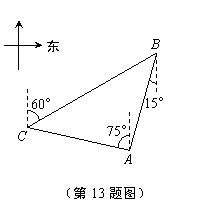
(A)20海里.
(B)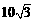 海里.
海里.
(C)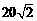 海里.
海里.
(D)30海里.
14.在平面直角坐标系中,函数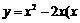 ≥
≥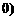 的图象为
的图象为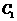 ,
,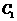 关于原点对称的图象为
关于原点对称的图象为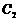 ,则直线
,则直线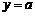 (a为常数)与
(a为常数)与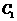 ,
,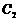 的交点共有
的交点共有
(A)1个.
(B)1个,或2个.
(C)1个,或2个,或3个.
(D)1个,或2个,或3个,或4个.
第Ⅱ卷(非选择题 共78分)
二、填空题(本大题共5小题,每小题3分,共15分)
15.在实数范围内分 解因式:
解因式: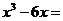 ___________ .
___________ .
16.某中学随机抽查了50名学生,了解他们一周的课外阅读时间,结果如下表所示:
时间(小时) | 4 | 5 | 6 | 7 |
人数 | 10 | 20 | 15 | 5 |
则这50名学生一周的平均课外阅读时间是___________小时.
17.如图,在 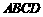 中,
中,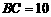 ,
,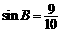 ,
,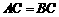 ,则
,则 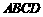 的面积是_________ .
的面积是_________ .
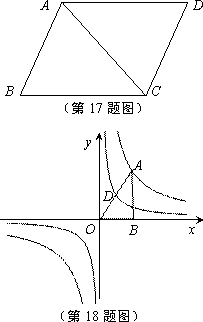
18.如图,反比例函数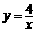 的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为__________.
的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为__________.
19.一般地,我们把研究对象统称为元素,把一些元素组成的总体称为集合.一个给定集合中的元素是互不相同的,也就是说,集合中的元素是不重复出现的.如一组数1,1,2,3,4就可以构成一个集合,记为A={1,2,3,4}.类比实数有加法运算,集合也可以“相加”.定义:集合A与集合B中的所有元素组成的集合称为集合A与集合B的和,记 为A+B. 若A ={-2,0,1,5,7},B ={-3,0,1,3,5},则A+B = __________.
为A+B. 若A ={-2,0,1,5,7},B ={-3,0,1,3,5},则A+B = __________.
三、解答题(本大题共7小题,共63分)
20.(本小题满分7分)
计算: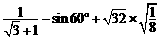 .
.
21.(本小题满分7分)
随着人民生活水平的提 高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选
高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选 一项):
一项):
A:加强交通法规学习;B:实行牌照管理;C:加大交通违法处罚力度;D:纳入机动车管理;E:分时间分路段限行.
调查 数据的部分统计结果如下表:
数据的部分统计结果如下表:
管理措施 | 回答人数 | 百分比 |
A | 25 | 5% |
B | 100 | m |
C | 75 | 15% |
D | n | 35% |
E | 125 | 25% |
合计 | a | 100% |
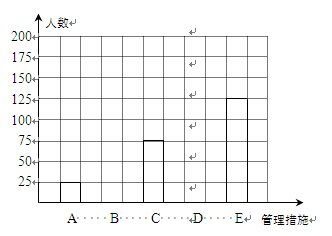
(1) 根据上述统计表中的数据可得m =_______,n =______,a =________;
根据上述统计表中的数据可得m =_______,n =______,a =________;
(2)在答题卡中,补全条形统计图;
(3)该社区有居民2600人,根据上述调查结果,请你估计选择“D:纳入机动车管理”的居民约有多少人?
22.(本小题满分7分)
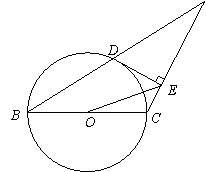
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作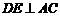 ,垂足为E.
,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
23.(本小题满分9分)
对一 张矩形纸片ABCD进行折叠,具体操作如下:
张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一 次折叠,使点A落
次折叠,使点A落 在MN上的点
在MN上的点 处,并使折痕经过点B,得到折痕BE,同时,得到线段
处,并使折痕经过点B,得到折痕BE,同时,得到线段 ,
, ,展开,如图1;
,展开,如图1;
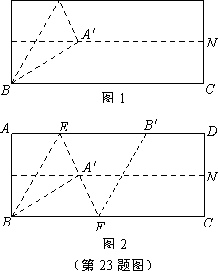
第三步:再沿 所在的直线折叠,点B落在AD上的点
所在的直线折叠,点B落在AD上的点 处,得到折痕EF,同时得到
处,得到折痕EF,同时得到 线段
线段 ,展开,如图2.
,展开,如图2.
(1)证明: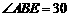 °;
°;
(2)证明:四边形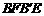 为菱形.
为菱形.
24.(本小题满分9分)
某景区的三个景点A,B,C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C. 甲 、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.
、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.
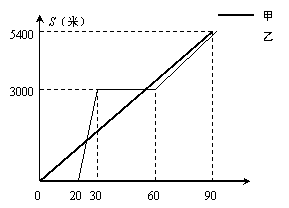
根据以上信息回答下列问题:
(1)乙出发后多长时间与甲相遇?
(2)要使甲到达景点C时,乙与C的路程不超过400米,则乙从景点B步行到景点C的速度至少为多少?
(结果精确到0.1米/分钟)
25.(本小题满分11分)
问题情境:如图1,四边形ABCD是正方形,M 是BC边上的一点,E是CD边的中点,AE平分
是BC边上的一点,E是CD边的中点,AE平分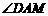 .
.
探究展示:
(1)证明: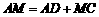 ;
;
(2)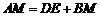 是否成立?若成立,请给出证明;若不成立,请说明理由.
是否成立?若成立,请给出证明;若不成立,请说明理由.
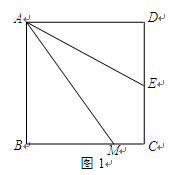
拓展延伸:
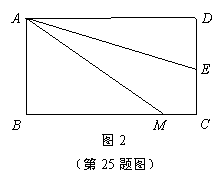
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别 作出判断,不需要证明.
作出判断,不需要证明.
26.(本小题满分1 3分)
3分)
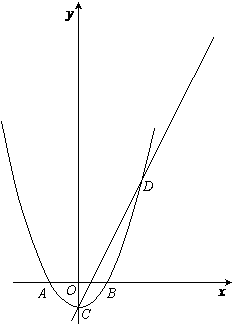
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线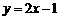 与y轴交于点C,
与y轴交于点C, 与抛物线交于点C,D.
与抛物线交于点C,D.
(1)求抛物线的解析式;
(2)求点A到直线CD的距离;
(3)平移抛物线,使抛物线的顶点P在直线CD上,抛物线与直线CD的另一个交点为Q,点G在y轴正半轴上,当以G,P,Q三点为顶点的三角形为等腰直角三角形时,求出所有符合条件的G点的坐标.


