(单词翻译:单击)
一.选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求.
1.(2013济宁)一运动员某次跳水的最高点离跳台2m,记作+2m,则水面离跳台10m可以记作( )
A.﹣10m B.﹣12m C.+10m D.+12m
考点:正数和负数.
分析:首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.
解答:解:跳水的最高点离跳台2m,记作+2m,
则水面离跳台10m可以记作﹣10m.
故选A.
点评:此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
2.(2013济宁)如果整式xn﹣2﹣5x+2是关于x的三次三项式,那么n等于( )
A.3 B.4 C.5 D.6
考点:多项式.
专题:计算题.
分析:根据题意得到n﹣2=3,即可求出n的值.
解答:解:由题意得:n﹣2=3,
解得:n=5.
故选C
点评:此题考查了多项式,熟练掌握多项式次数的定义是解本题的关键.
3.(2013济宁)2013年国家财政支出将大幅向民生倾斜,民生领域里流量最大的开销是教育,预算支出达到23 000多亿元.将23 000用科学记数法表示应为( )
A.2.3×104 B.0.23×106 C.2.3×105 D.23×104
考点:科学记数法—表示较大的数.
分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答:解:23 000=2.3×104,
故选A.
点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(2013济宁)已知ab=4,若﹣2≤b≤﹣1,则a的取值范围是( )
A.a≥﹣4 B.a≥﹣2 C.﹣4≤a≤﹣1 D.﹣4≤a≤﹣2
考点:不等式的性质.
分析:根据已知条件可以求得b=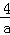 ,然后将b的值代入不等式﹣2≤b≤﹣1,通过解该不等式即可求得a的取值范围.
,然后将b的值代入不等式﹣2≤b≤﹣1,通过解该不等式即可求得a的取值范围.
解答:解:由ab=4,得
b=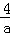 ,
,
∵﹣2≤b≤﹣1,
∴﹣2≤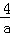 ≤﹣1,
≤﹣1,
∴﹣4≤a≤﹣2.
故选D.
点评:本题考查的是不等式的基本性质,不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
5.(2013济宁)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
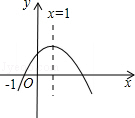
A.a>0 B.当﹣1<x<3时,y>0
C.c<0 D.当x≥1时,y随x的增大而增大
考点:二次函数图象与系数的关系.
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:A.抛物线的开口方向向下,则a<0.故本选项错误;
B.根据图示知,抛物线的对称轴为x=1,抛物线与x轴的一交点的横坐标是﹣1,则抛物线与x轴的另一交点的横坐标是3,
所以当﹣1<x<3时,y>0.故本选项正确;
C.根据图示知,该抛物线与y轴交与正半轴,则c>0.故本选项错误;
D.根据图示知,当x≥1时,y随x的增大而减小,故本选项错误.
故选B.
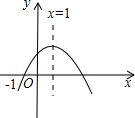
点评:本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.
6.(2013济宁)下列说法正确的是( )
A.中位数就是一组数据中最中间的一个数
B.8,9,9,10,10,11这组数据的众数是9
C.如果x1,x2,x3,…,xn的平均数是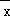 ,那么(x1﹣
,那么(x1﹣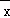 )+(x2﹣
)+(x2﹣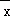 )+…+(xn﹣
)+…+(xn﹣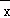 )=0
)=0
D.一组数据的方差是这组数据的极差的平方
考点:方差;算术平均数;中位数;众数;极差.
分析:根据中位数以及众数和平均数和极差、方差的定义分别判断得出即可.
解答:解:A.当数据是奇数个时,按大小排列后,中位数就是一组数据中最中间的一个数,数据个数为偶数个时,按大小排列后,最中间的两个的平均数是中位数,故此选项错误;
B.8,9,9,10,10,11这组数据的众数是9和10,故此选项错误;
C.如果x1,x2,x3,…,xn的平均数是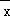 ,那么(x1﹣
,那么(x1﹣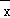 )+(x2﹣
)+(x2﹣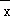 )+…+(xn﹣
)+…+(xn﹣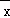 )=x1+x2+x3+…+xn﹣n
)=x1+x2+x3+…+xn﹣n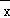 =0,故此选项正确;
=0,故此选项正确;
D.一组数据的方差与极差没有关系,故此选项错误;
故选:C.
点评:此题主要考查了中位数以及众数和平均数和极差、方差的定义,根据定义举出反例是解题关键.
7.(2013济宁)服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的标价比进价多( )
A.60元 B.80元 C.120元 D.180元
考点:一元一次方程的应用.
分析:设这款服装的进价为x元,就可以根据题意建立方程300×0.8﹣x=60,就可以求出进价,再用标价减去进价就可以求出结论.
解答:解:设这款服装的进价为x元,由题意,得
300×0.8﹣x=60,
解得:x=180.
300﹣180=120,
∴这款服装每件的标价比进价多120元.
故选C.
点评:本题时一道销售问题.考查了列一元一次方程解实际问题的运用,利润=售价﹣进价的运用,解答时根据销售问题的数量关系建立方程是关键.
8.(2013济宁)如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
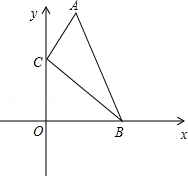
A.(0,0) B.(0,1) C.(0,2) D.(0,3)
考点:轴对称-最短路线问题;坐标与图形性质.
分析:根据轴对称做最短路线得出AE=BE,进而得出B′O=C′O,即可得出△ABC的周长最小时C点坐标.
解答:解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,
此时△ABC的周长最小,
∵点A、B的坐标分别为(1,4)和(3,0),
∴B′点坐标为:(﹣3,0),AE=4,
则BE=4,即BE=AE,
∵C′O∥AE,
∴B′O=C′O=3,
∴点C′的坐标是(0,3),此时△ABC的周长最小.
故选:D.
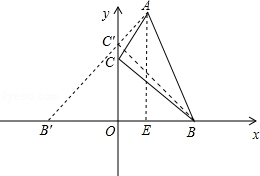
点评:此题主要考查了利用轴对称求最短路线以及平行线的性质,根据已知得出C点位置是解题关键.
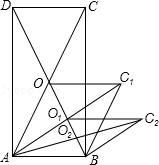
9.(2013济宁)如图,矩形ABCD的面积为20cm2,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )
A.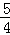 cm2 B.
cm2 B.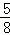 cm2 C.
cm2 C.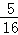 cm2 D.
cm2 D.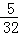 cm2
cm2
考点:矩形的性质;平行四边形的性质.
专题:规律型.
分析:根据矩形的对角线互相平分,平行四边形的对角线互相平分可得下一个图形的面积是上一个图形的面积的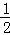 ,然后求解即可.
,然后求解即可.
解答:解:设矩形ABCD的面积为S=20cm2,
∵O为矩形ABCD的对角线的交点,
∴平行四边形AOC1B底边AB上的高等于BC的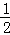 ,
,
∴平行四边形AOC1B的面积=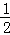 S,
S,
∵平行四边形AOC1B的对角线交于点O1,
∴平行四边形AO1C2B的边AB上的高等于平行四边形AOC1B底边AB上的高的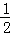 ,
,
∴平行四边形AO1C2B的面积=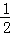 ×
×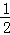 S=
S=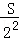 ,
,
…,
依此类推,平行四边形AO4C5B的面积=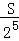 =
=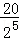 =
=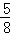 cm2.
cm2.
故选B.
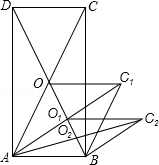
点评:本题考查了矩形的对角线互相平分,平行四边形的对角线互相平分的性质,得到下一个图形的面积是上一个图形的面积的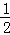 是解题的关键.
是解题的关键.
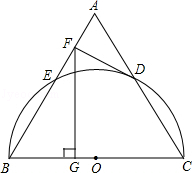
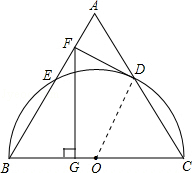
10.(2013济宁)如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
A.4 B.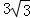 C.6 D.
C.6 D.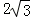
考点:切线的性质;等边三角形的性质;含30度角的直角三角形;勾股定理;圆周角定理.
专题:计算题.
分析:连接OD,由DF为圆的切线,利用切线的性质得到OD垂直于DF,根据三角形ABC为等边三角形,利用等边三角形的性质得到三条边相等,三内角相等,都为60°,由OD=OC,得到三角形OCD为等边三角形,进而得到OD平行与AB,由O为BC的中点,得到D为AC的中点,在直角三角形ADF中,利用30°所对的直角边等于斜边的一半求出AD的长,进而求出AC的长,即为AB的长,由AB﹣AF求出FB的长,在直角三角形FBG中,利用30°所对的直角边等于斜边的一半求出BG的长,再利用勾股定理即可求出FG的长.
解答:解:连接OD,
∵DF为圆O的切线,
∴OD⊥DF,
∵△ABC为等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵OD=OC,
∴△OCD为等边三角形,
∴OD∥AB,
又O为BC的中点,
∴D为AC的中点,即OD为△ABC的中位线,
∴OD∥AB,
∴DF⊥AB,
在Rt△AFD中,∠ADF=30°,AF=2,
∴AD=4,即AC=8,
∴FB=AB﹣AF=8﹣2=6,
在Rt△BFG中,∠BFG=30°,
∴BG=3,
则根据勾股定理得:FG=3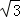 .
.
故选B
点评:此题考查了切线的性质,等边三角形的性质,含30°直角三角形的性质,勾股定理,熟练掌握切线的性质是解本题的关键.
二.填空题(共5小题,每小题3分,满分15分)
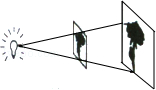
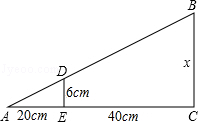
11.(2013济宁)如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 cm.
考点:相似三角形的应用.
分析:根据题意可画出图形,再根据相似三角形的性质对应边成比例解答.
解答:解:∵DE∥BC,
∴△AED∽△ABC
∴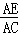 =
=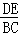
设屏幕上的小树高是x,则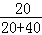 =
=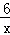
解得x=18cm.故答案为:18.
点评:本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
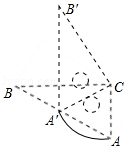
12.(2013济宁)如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
考点:旋转的性质;弧长的计算.
分析:根据Rt△ABC中的30°角所对的直角边是斜边的一半、直角三角形斜边上的中线等于斜边的一半以及旋转的性质推知△AA′C是等边三角形,所以根据等边三角形的性质利用弧长公式来求CA′旋转所构成的扇形的弧长.
解答:解:∵在Rt△ABC中,∠B=30°,AB=10cm,
∴AC=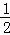 AB=5cm.
AB=5cm.
根据旋转的性质知,A′C=AC,
∴A′C=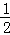 AB=5cm,
AB=5cm,
∴点A′是斜边AB的中点,
∴AA′=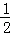 AB=5cm,
AB=5cm,
∴AA′=A′C=AC,
∴∠A′CA=60°,
∴CA′旋转所构成的扇形的弧长为: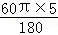 =
=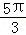 (cm).
(cm).
故答案是: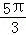 .
.
点评:本题考查了弧长的计算、旋转的性质.解题的难点是推知点A′是斜边AB的中点,同时,这也是解题的关键.
13.(2013济宁)甲、乙、丙三人站成一排合影留念,则甲、乙二人相邻的概率是 .
考点:列表法与树状图法.
分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲、乙二人相邻的情况,再利用概率公式求解即可求得答案.
解答:解:画树状图得: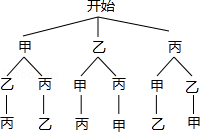
∵共有6种等可能的结果,甲、乙二人相邻的有4种情况,
∴甲、乙二人相邻的概率是: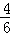 =
=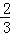 .
.
故答案为: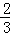 .
.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
14.(2013济宁)三棱柱的三视图如图所示,△EFG中,EF=8cm,EG=12cm,∠EGF=30°,则AB的长为 cm.
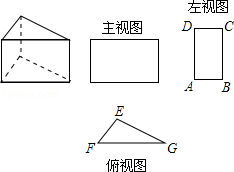
考点:由三视图判断几何体.
分析:根据三视图的对应情况可得出,△EFGFG上的高即为AB的长,进而求出即可.
解答:解:过点E作EQ⊥FG于点Q,
由题意可得出:FQ=AB,
∵EG=12cm,∠EGF=30°,
∴EQ=AB=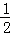 ×12=6(cm).
×12=6(cm).
故答案为:6.
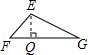
点评:此题主要考查了由三视图解决实际问题,根据已知得出FQ=AB是解题关键.
15.(2013济宁)在我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(倍加增指从塔的顶层到底层).请你算出塔的顶层有 盏灯.
考点:一元一次方程的应用.
分析:根据题意,假设顶层的红灯有x盏,则第二层有2x盏,依次第三层有4x盏,第四层有8x盏,第五层有16x盏,第六层有32x盏,第七层有64x盏,总共381盏,列出等式,解方程,即可得解.
解答:解:假设尖头的红灯有x盏,由题意得:x+2x+4x+8x+16x+32x+64x=381,
127x=381,
x=3(盏);
答:塔的顶层是3盏灯.
故答案为:3.
点评:此题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.
三.解答题:本大题共8小题,共55分.
16.(2013济宁)计算:(2﹣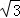 )2012(2+
)2012(2+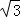 )2013﹣2
)2013﹣2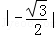 ﹣(
﹣(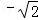 )0.
)0.
考点:二次根式的混合运算;零指数幂.
分析:根据零指数幂、绝对值、整数指数幂、二次根式的混合运算,分别进行计算,再把所得的结果合并即可.
解答:解:(2﹣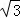 )2012(2+
)2012(2+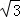 )2013﹣2
)2013﹣2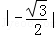 ﹣(
﹣(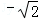 )0=[(2﹣
)0=[(2﹣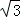 )(2+
)(2+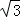 )]2012(2+
)]2012(2+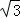 )﹣
)﹣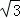 ﹣1
﹣1
=2+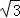 ﹣
﹣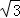 ﹣1
﹣1
=1.
点评:此题考查了二次根式的混合运算,用到的知识点是零指数幂、绝对值、整数指数幂、二次根式的混合运算,关键是熟练掌握有关知识和公式.
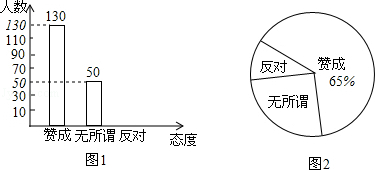
17.(2013济宁)以“光盘”为主题的公益活动越来越受到社会的关注.某校为培养学生勤俭节约的习惯,随机抽查了部分学生(态度分为:赞成、无所谓、反对),并将抽查结果绘制成图1和图2(统计图不完整).请根据图中提供的信息,解答下列问题:(1)此次抽样调查中,共抽查了多少名学生?
(2)将图1补充完整;
(3)根据抽样调查结果,请你估计该校3000名学生中有多少名学生持反对态度?
考点:条形统计图;用样本估计总体;扇形统计图.
分析:(1)根据赞成是130人,占65%即可求得总人数;
(2)利用总人数减去另外两项的人数,求得反对的人数,从而作出统计图;
(3)利用3000乘以持反对态度的比例即可.
解答:解:(1)130÷65%=200名;
(2)200﹣130﹣50=20名;
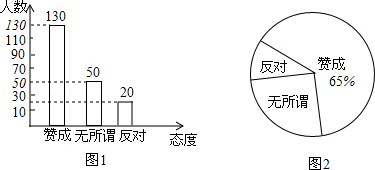
(3)3000×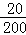 =300名.
=300名.
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
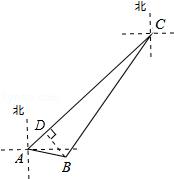
18.(2013济宁)钓鱼岛及其附属岛屿是中国固有领土(如图1),A、B、C分别是钓鱼岛、南小岛、黄尾屿上的点(如图2),点C在点A的北偏东47°方向,点B在点A的南偏东79°方向,且A、B两点的距离约为5.5km;同时,点B在点C的南偏西36°方向.若一艘中国渔船以30km/h的速度从点A驶向点C捕鱼,需要多长时间到达(结果保留小数点后两位)?(参考数据:sin54°≈0.81,cos54°≈0.59,tan47°≈1.07,tan36°≈0.73,tan11°≈0.19)
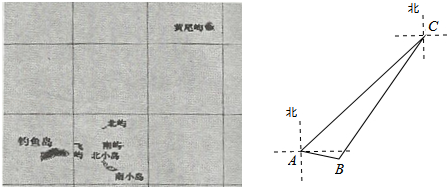
考点:解直角三角形的应用-方向角问题.
分析:过点B作BD⊥AC交AC于点D,根据方向角分别求出∠DAB和∠DCB的度数,然后在Rt△ABD和Rt△BCD中,分别解直角三角形求出AD、CD的长度,然后根据时间=路程÷速度即可求出需要的时间.
解答:解:过点B作BD⊥AC交AC于点D,
由题意得,∠DAB=180°﹣47°﹣79°=54°,
∠DCB=47°﹣36°=11°,
在Rt△ABD中,
∵AB=5.5,∠DAB=54°,
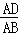 =cos54°,
=cos54°,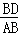 =sin54°,
=sin54°,
∴AD=5.5×0.59=3.245,BD=4.445,
在Rt△BCD中,
∵BD=4.445,∠DCB=11°,
∴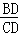 =tan11°,
=tan11°,
∴CD=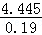 =23.394,
=23.394,
∴AC=AD+CD=3.245+23.394≈26.64(km),
则时间t=26.64÷30≈0.90(h).
答:需要0.90h到达.
点评:本题考查了解直角三角形的应用,难度适中,解答本题的关键是构造直角三角形并解直角三角形,
19.(2013济宁)人教版教科书对分式方程验根的归纳如下:“解分式方程时,去分母后所得整式方程的解有可能使原分式方程中的分母为0,因此应如下检验:将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.”
请你根据对这段话的理解,解决下面问题:已知关于x的方程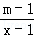 ﹣
﹣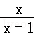 =0无解,方程x2+kx+6=0的一个根是m.
=0无解,方程x2+kx+6=0的一个根是m.
(1)求m和k的值;
(2)求方程x2+kx+6=0的另一个根.
考点:解分式方程;根与系数的关系.
专题:阅读型.
分析:(1)分式方程去分母转化为整式方程,由分式方程无解,故将x=1代入整式方程,即可求出m的值,将m的值代入已知方程即可求出k的值;
(2)利用根与系数的关系即可求出方程的另一根.
解答:解:(1)分式方程去分母得:m﹣1﹣x=0,
由题意将x=1代入得:m﹣1﹣1=0,即m=2,
将m=2代入方程得:4+2k+6=0,即k=﹣5;
(2)设方程另一根为a,则有2a=6,即a=3.
点评:此题考查了解分式方程,以及根与系数的关系,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.
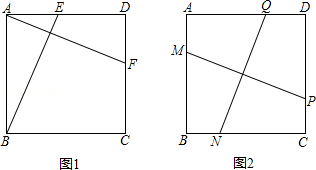
20.(2013济宁)如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
考点:正方形的性质;全等三角形的判定与性质.
专题:证明题.
分析:(1)根据正方形的性质可得AB=AD,∠BAE=∠D=90°,再根据同角的余角相等求出∠ABE=∠DAF,然后利用“角边角”证明△ABE和△DAF全等,再根据全等三角形的证明即可;
(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,然后与(1)相同.
解答:(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°,
∵AF⊥BE,
∴∠ABE+∠BAF=90°,
∴∠ABE=∠DAF,
∵在△ABE和△DAF中,
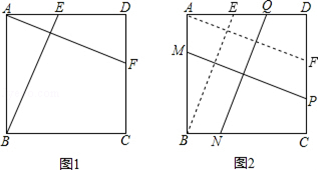
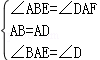 ,
,
∴△ABE≌△DAF(ASA),
∴AF=BE;
(2)解:MP与NQ相等.
理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,
则与(1)的情况完全相同.
点评:本题考查了正方形的性质,全等三角形的判定与性质,主要利用了正方形的四条边都相等,每一个角都是直角的性质,同角的余角相等的性质,利用三角形全等证明相等的边是常用的方法之一,要熟练掌握并灵活运用.
21.(2013济宁)阅读材料:若a,b都是非负实数,则a+b≥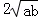 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵(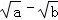 )2≥0,∴a﹣
)2≥0,∴a﹣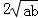 +b≥0.
+b≥0.
∴a+b≥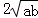 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:已知x>0,求函数y=2x+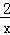 的最小值.
的最小值.
解:y=2x+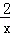 ≥
≥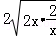 =4.当且仅当2x=
=4.当且仅当2x=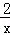 ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数取得最小值,y最小=4.
问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(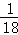 +
+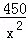 )升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
考点:反比例函数的应用;一元一次不等式的应用.
分析:(1)根据耗油总量=每公里的耗油量×行驶的速度列出函数关系式即可;
(2)经济时速就是耗油量最小的形式速度.
解答:解:(1)∵汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(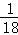 +
+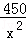 )升.
)升.
∴y=x×(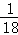 +
+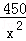 )=
)=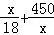 (70≤x≤110);
(70≤x≤110);
(2)根据材料得:当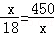 时有最小值,
时有最小值,
解得:x=90
∴该汽车的经济时速为90千米/小时;
当x=90时百公里耗油量为100×(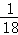 +
+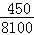 )≈11.1升,
)≈11.1升,
点评:本题考查了反比例函数的应用,解题的关键是读懂题目提供的材料.
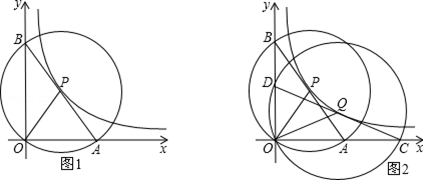
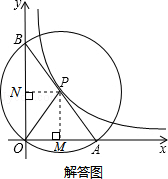
22.(2013济宁)如图1,在平面直角坐标系中,O为坐标原点,P是反比例函数y=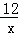 (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
(3)如图2,Q是反比例函数y=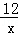 (x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.
(x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.
求证:DO•OC=BO•OA.
考点:反比例函数综合题.
分析:(1)∠AOB=90°,由圆周角定理的推论,可以证明AB是⊙P的直径;
(2)将△AOB的面积用含点P坐标的表达式表示出来,容易计算出结果;
(3)对于反比例函数上另外一点Q,⊙Q与坐标轴所形成的△COD的面积,依然不变,与△AOB的面积相等.
解答:(1)证明:∵∠AOB=90°,且∠AOB是⊙P中弦AB所对的圆周角,
∴AB是⊙P的直径.
(2)解:设点P坐标为(m,n)(m>0,n>0),
∵点P是反比例函数y=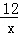 (x>0)图象上一点,∴mn=12.
(x>0)图象上一点,∴mn=12.
如答图,过点P作PM⊥x轴于点M,PN⊥y轴于点N,则OM=m,ON=n.
由垂径定理可知,点M为OA中点,点N为OB中点,
∴OA=2OM=2m,OB=2ON=2n,
∴S△AOB= BO•OA=
BO•OA=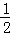 ×2n×2m=2mn=2×12=24.
×2n×2m=2mn=2×12=24.
(3)证明:若点Q为反比例函数y=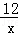 (x>0)图象上异于点P的另一点,
(x>0)图象上异于点P的另一点,
参照(2),同理可得:S△COD=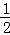 DO•CO=24,
DO•CO=24,
则有:S△COD=S△AOB=24,即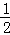 BO•OA=
BO•OA=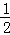 DO•CO,
DO•CO,
∴DO•OC=BO•OA.
点评:本题考查了反比例函数的图象与性质、圆周角定理、垂径定理等知识,难度不大.试题的核心是考查反比例函数系数的几何意义.对本题而言,若反比例函数系数为k,则可以证明⊙P在坐标轴上所截的两条线段的乘积等于4k;对于另外一点Q所形成的⊙Q,此结论依然成立.
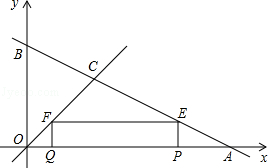
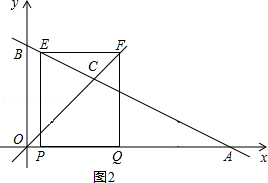
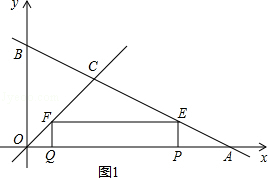
23.(2013济宁)如图,直线y=﹣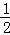 x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
(1)求点P运动的速度是多少?
(2)当t为多少秒时,矩形PEFQ为正方形?
(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.
考点:一次函数综合题.
分析:(1)根据直线y=﹣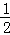 x+4与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出
x+4与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出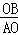 =
=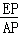 =
=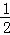 ,据此可以求得点P的运动速度;
,据此可以求得点P的运动速度;
(2)当PQ=PE时,以及当PQ=PE时,矩形PEFQ为正方形,分别求出即可;
(3)根据(2)中所求得出s与t的函数关系式,进而利用二次函数性质求出即可.
解答:解:(1)∵直线y=﹣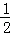 x+4与坐标轴分别交于点A、B,
x+4与坐标轴分别交于点A、B,
∴x=0时,y=4,y=0时,x=8,
∴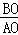 =
=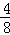 =
= ,
,
当t秒时,QO=FQ=t,则EP=t,
∵EP∥BO,
∴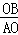 =
=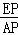 =
= ,
,
∴AP=2t,
∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,
∴点P运动的速度是每秒2个单位长度;
(2)如图1,当PQ=PE时,矩形PEFQ为正方形,
则∵OQ=FQ=t,PA=2t,
∴QP=8﹣t﹣2t=8﹣3t,
∴8﹣3t=t,
解得:t=2,
如图2,当PQ=PE时,矩形PEFQ为正方形,
∵OQ=t,PA=2t,
∴OP=8﹣2t,
∴QP=t﹣(8﹣2t)=3t﹣8,
∴t=3t﹣8,
解得:t=4;
(3)如图1,当Q在P点的左边时,
∵OQ=t,PA=2t,
∴QP=8﹣t﹣2t=8﹣3t,
∴S矩形PEFQ=QP•QF=(8﹣3t)•t=8t﹣3t2,
当t=﹣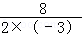 =
=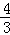 时,
时,
S矩形PEFQ的最大值为: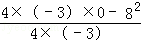 =4,
=4,
如图2,当Q在P点的右边时,
∵OQ=t,PA=2t,
∴QP=t﹣(8﹣2t)=3t﹣8,
∴S矩形PEFQ=QP•QE=(3t﹣8)•t=3t2﹣8t,
∵当点P、Q其中一点停止运动时,另一点也停止运动,
∴0≤t≤4,
当t=﹣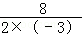 =
=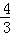 时,S矩形PEFQ的最小,
时,S矩形PEFQ的最小,
∴t=4时,S矩形PEFQ的最大值为:3×42﹣8×4=16,
综上所述,当t=4时,S矩形PEFQ的最大值为:16.
点评:此题主要考查了二次函数与一次函数的综合应用,得出P,Q不同的位置进行分类讨论得出是解题关键.


