(单词翻译:单击)
一、仔细选一选(本题有10个小题,每小题3分,共30分)
下面每个小题给出的四个选项中,只有一个是正确的,请把正确的选项所对应的字母在答题卷中相应的格子涂黑,注意可用多种不同的方法来选取正确答案。
1. 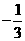 的倒数是
的倒数是
A. 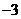 B. 3 C.
B. 3 C. 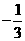 D.
D. 
2.磁湖是黄石一颗璀璨的明珠,据统计,在今年“五一”期间,游览磁湖的人数为21.22万人,这一数据用科学记数法可表示为
A. 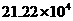 人 B.
人 B. 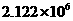 人
人
C. 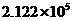 人 D.
人 D. 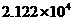 人
人
3.下列计算正确的是
A. B.
B. 
C. 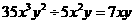 D.
D. 
4.如图,一个正方体被截去四个角后得到一个几何体,它的俯 视图是
视图是
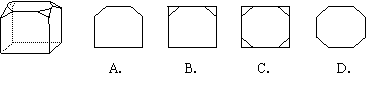
5.如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是

A.30° B. 60° C. 90° D. 120°
6.学校团委在“五四青年节”举行“感动校园十大人物”颁奖活动中,九(4)班决定从甲、乙、丙、丁四人中随机派两名代表参加此活动,则甲乙两人恰有一人参加此活动的概率是
A.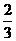 B.
B. C.
C.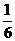 D.
D.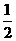
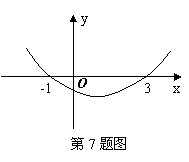
7.二次函数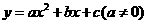 的图像
的图像 如图所示,则函数值
如图所示,则函数值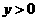 时,x的取值范围是
时,x的取值范围是
A.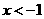 B.
B. 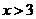
C.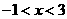 D.
D. 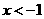 或
或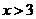
8.以下命题是真命题的是
A. 梯形是轴对称图形 B. 对角线相等的四边形是矩形
C. 四边相等的四边形是正方形 D. 有两条相互垂直的对称轴的四边形是菱形
9.正方形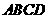 在直角坐标系中的位置如下图表示,将正方形
在直角坐标系中的位置如下图表示,将正方形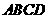 绕点
绕点 顺时针方向旋转180°后,
顺时针方向旋转180°后,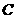 点的坐标是
点的坐标是
A. B.
B. 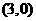 C.
C.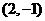 D.
D.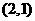
10.如图,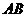 是半圆
是半圆 的直径,点
的直径,点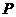 从点
从点 出发,沿半圆弧
出发,沿半圆弧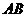 顺时针方向匀速移动至点
顺时针方向匀速移动至点 ,运动时间为
,运动时间为 ,△
,△ 的面积为
的面积为 ,则下列图像能大致刻画
,则下列图像能大致刻画 与
与 之间的关系的是
之间的关系的是

二、认真填一填(本题有6个小题,每小题3分,共18分)
11. 函数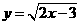 中自变量
中自变量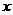 是取值范围是______________.
是取值范围是______________.
12. 分解因式: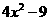 =______________.
=______________.
13. 如下图,圆 的直径
的直径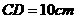 ,且
,且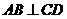 ,垂足为
,垂足为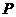 ,
,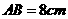 ,则
,则 ______________ .
______________ .

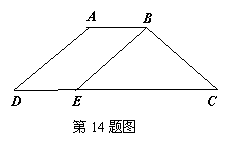
14. 如下图,在等腰梯形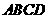 中,
中, ,
,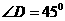 ,
, ,
, 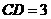 ,
, 交
交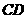 于
于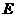 ,则△
,则△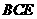 的周长为______________.
的周长为______________.
15. 一般地,如果在一次实验中,结果落在区域 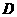 中每一个点都是等可能的,用
中每一个点都是等可能的,用  表示“实验结果落在
表示“实验结果落在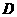 中的某个小区域
中的某个小区域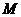 中”这个事件,那么事件
中”这个事件,那么事件 发生的概率
发生的概率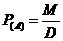 。如上图,现在等边△
。如上图,现在等边△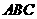 内射入一个点,则该点落在△
内射入一个点,则该点落在△
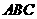 内切圆中的概率是 ______________.
内切圆中的概率是 ______________.

16.观察下列等式:
第一个等式: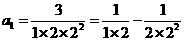
第二个等式: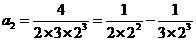
第三个等式: 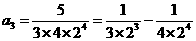
第四个等式: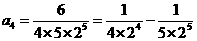
按上述规律,回答以下问题:
(1)用含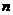 的代数式表示第
的代数式表示第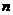 个等式:
个等式: ______________
______________  ______________;
______________;
(2)式子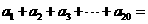 ______________.
______________.
三、全面答一答(本题有9个小题,共72分)
解答应写出文字说明,证明过 程或推演步骤,如果觉得有的题目有点困难,那么把自己能写出的解答尽量写出来。
程或推演步骤,如果觉得有的题目有点困难,那么把自己能写出的解答尽量写出来。
17.(本小题满分7分)计算: 
18.(本小题满分7分)先化简,后计算: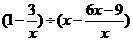 ,其中
,其中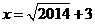 .
.
19.(本小题满分7分)如图, 、
、 是圆
是圆 上的两点,
上的两点,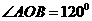 ,
,  是
是 弧的中点.
弧的中点.
(1)求证: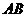 平分
平分 ;
;
(2)延长 至
至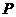 使得
使得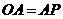 ,连接
,连接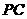 ,若圆
,若圆 的半径
的半径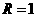 ,求
,求 的长.
的长.
20.(本小题满分8分)解方程:
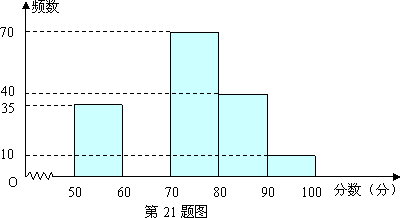
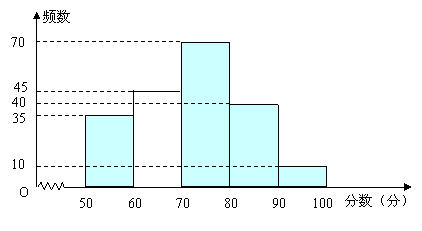
21.(本小题满分8分)为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作 品打分发现,参赛者的成绩
品打分发现,参赛者的成绩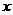 均满足
均满足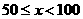 ,并制作了频数分布直方图,如右图.
,并制作了频数分布直方图,如右图.
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩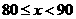 的选手中应抽多少人?
的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
22.(本小题满分8分)小明听说“武黄城际列车”已经开通.便设计了如下问题:如下图,以往从黄石 坐客车到武昌客运站
坐客车到武昌客运站 ,现在可以在
,现在可以在 坐城际列车到武汉青山站
坐城际列车到武汉青山站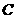 ,再从青山站
,再从青山站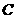 坐市内公共汽车到武昌客运站
坐市内公共汽车到武昌客运站 。设
。设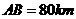 ,
, ,
,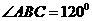 .请你帮助小明解决以下问题:
.请你帮助小明解决以下问题:
(1)求 、
、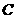 之间的距离;(参考数据
之间的距离;(参考数据 );
);
(2)若客车的平均速度是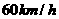 ,市内的公共汽车的平均速度为
,市内的公共汽车的平均速度为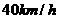 ,城际列车的平均速度为
,城际列车的平均速度为 ,为了最短时间到达武昌客运站,小明应该选择哪种乘车方案?请说明理由.(不计候车时间)
,为了最短时间到达武昌客运站,小明应该选择哪种乘车方案?请说明理由.(不计候车时间)
23.(本小题满分8分)某校九(3)班去大冶茗山乡 花卉基地参加社会实践活动,该基地有玫瑰花和蓑衣草两种花卉,活动后,小明编制了一道数学题:花卉基地有甲乙两家种植户,种植面积与卖花总收入如下表.(假设不同种植户种植的同种花卉每亩卖花平均收入相等)
花卉基地参加社会实践活动,该基地有玫瑰花和蓑衣草两种花卉,活动后,小明编制了一道数学题:花卉基地有甲乙两家种植户,种植面积与卖花总收入如下表.(假设不同种植户种植的同种花卉每亩卖花平均收入相等)
种植户 | 玫瑰花种植面积(亩) | 蓑衣草种植面积(亩) | 卖花总收入(元) |
甲 | 5 | 3 | 33500 |
乙 | 3 | 7 | 43500 |
(1)试求玫瑰花,蓑衣草每亩卖花的平均收入各是多少?
(2 )甲、乙种植户计划合租30亩地用来种植玫瑰花和蓑衣草,根据市场调查,要求玫瑰花的种植面积大于蓑衣草的种植面积(两种花卉的种植面积均为整数亩),花卉基地对种植玫瑰花的种植给予补贴,种
)甲、乙种植户计划合租30亩地用来种植玫瑰花和蓑衣草,根据市场调查,要求玫瑰花的种植面积大于蓑衣草的种植面积(两种花卉的种植面积均为整数亩),花卉基地对种植玫瑰花的种植给予补贴,种 植玫瑰花的面积不超过15亩的部分,每亩补贴100元;超过15亩但不超过20亩的部分,每亩补贴200元;超过20亩的部分每亩补贴300元.为了使总收入不低于127500元,则他们有几种种植方案?
植玫瑰花的面积不超过15亩的部分,每亩补贴100元;超过15亩但不超过20亩的部分,每亩补贴200元;超过20亩的部分每亩补贴300元.为了使总收入不低于127500元,则他们有几种种植方案?
24.(本小题满分9分) 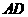 是△
是△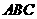 的中线,将
的中线,将 边所在直线绕点
边所在直线绕点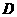 顺时针旋转
顺时针旋转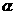 角,交边
角,交边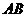 于点
于点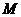 ,交射
,交射 线
线 于点
于点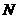 ,设
,设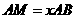 ,
,
 .
.
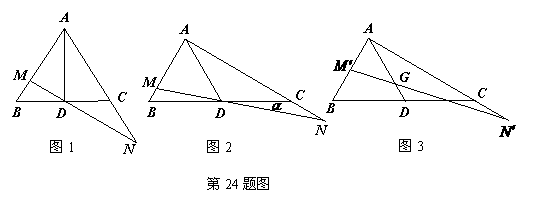
(1)如图1,当△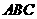 为等边三角形且
为等边三角形且 时证明:△
时证明:△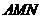 ∽△
∽△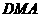 ;
;
(2)如图2,证明: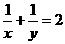 ;
;
(3)如图3,当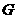 是
是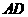 上任意一点时(点
上任意一点时(点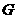 不与
不与 重合),过点
重合),过点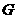 的直线交边
的直线交边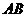 于
于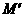 ,交射线
,交射线 于点
于点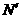 ,设
,设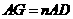 ,
,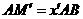 ,
,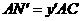
 ,猜想:
,猜想: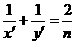 是否成立?并说明理由.
是否成立?并说明理由.
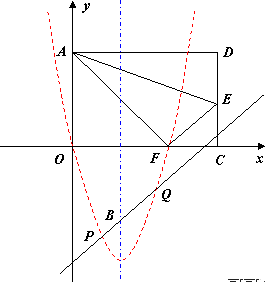
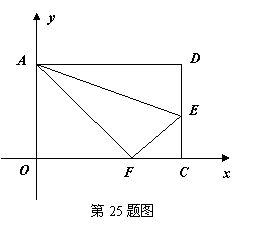
25.(本小题满分10分)如图,在矩形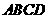 中,把点
中,把点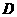 沿
沿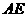 对折,使点
对折,使点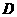 落在
落在 上的
上的 点,已知
点,已知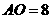 。
。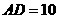 .
.
(1)求 点的坐标;
点的坐标;
(2)如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点,我们把这条直线称为抛物线的切线,已知抛物线经过点 ,
, ,且直线
,且直线 是该抛物线的切线,求抛物线的解析式;
是该抛物线的切线,求抛物线的解析式;
(3)直线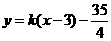 与(2)中的抛物线交于
与(2)中的抛物线交于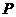 、
、 两点,点
两点,点 的坐标为
的坐标为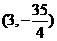 ,求证:
,求证: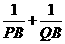 为定值(参考公式:在平面直角坐标系中,若
为定值(参考公式:在平面直角坐标系中,若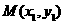 ,
,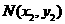 ,则
,则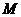 ,
,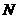 两点间的距离为
两点间的距离为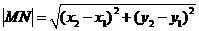 )
)
黄石市2014年初中毕业生学业考试
数学答案及评分说明
一、选择题(每小题3分,共30分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | C | C | C | C | A | D | D | B | C |
二、填空题(每小题3分,共18分)
11. 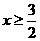 12.
12.  13.
13.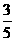
14.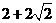 15.
15.
 16.
16.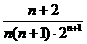 ,
,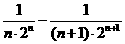 ,
,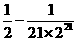
三、解答题(9小题,共72分)
17.(7分)解:原式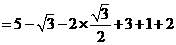 ··············· (5分)
··············· (5分)
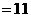 ························· (2分)
························· (2分)
18.(7分)解:原式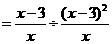
 ······················· (5分)
······················· (5分)
当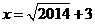 时,原式
时,原式
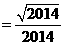 ( 2分)
( 2分)
19.(1)证明:∵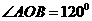 ,
,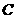 是
是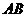 弧的中点
弧的中点
∴

∴四边形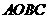 是菱形
是菱形
∴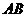 平分
平分 ······················· (4分)
······················· (4分)
(2)解:由(1)知,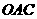 是等边三角形
是等边三角形
∵
∴
∴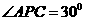
∴△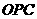 是直角三角形
是直角三角形
∴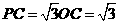 ······················ (3分)
······················ (3分)
20.(8分)解:依题意
由(2)得 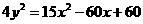 (3)
(3)
将(3)代入(1)化简得 ············ (4分)
············ (4分)
解此方程得 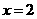 或
或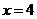 (2分)
(2分)
代入(2)得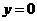 或
或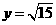
∴原方程 组的解为
组的解为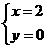 或
或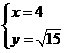 ············· (2分)
············· (2分)
21.(8分)解:(1)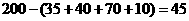 ,如下图:········ (3分)
,如下图:········ (3分)
(2)设抽了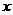 人,则
人,则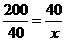 ,解得
,解得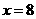 ·············· (3分)
·············· (3分)
(3)依题意知获一等奖的人数为 %
%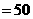 ············ (2分)
············ (2分)
22.(8分)解:(1)过点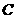 作
作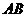 的垂线,交
的垂线,交 的延长线于
的延长线于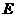 点,
点,
∵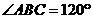 ,
,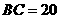
∴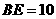 ,
,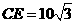
在△ 中,
中,
∵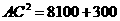
∴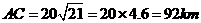 ··················· (4分)
··················· (4分)
(2)乘客车需时间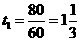 (小时)················ (2分)
(小时)················ (2分)
乘列车需时间 (小时)
(小时)
∴选择城际列车··························· (2分)
23.(8分)解:(1)设玫瑰花,蓑 衣草的亩平均收入分别为
衣草的亩平均收入分别为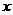 ,
,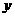 元,依题意得:
元,依题意得:
 )························ (2分)
)························ (2分)
解得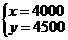 ·························· (2分)
·························· (2分)
(2)设种植玫瑰花 亩,则种植蓑衣草面积为
亩,则种植蓑衣草面积为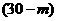 亩,依题意得
亩,依题意得
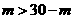 得
得 
当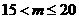 时,总收入
时,总收入
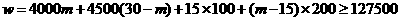
解得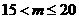 ····················· (2分)
····················· (2分)
当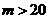 时,总收入
时,总收入
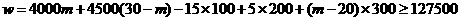 解得
解得 不合题意 (1分)
不合题意 (1分)
综上所述,种植方案如下:
种植类型 | 种植面积(亩) | ||||
方案一 | 方案二 | 方案三 | 方案四 | 方案五 | |
玫瑰花 | 16 | 17 | 18 | 19 | 20 |
蓑衣草 | 14 | 13 | 12 | 11 | 10 |
····························· (1分)
24.(9分)解:(1)证明:在△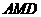 中,
中,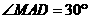 ,
,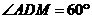
∴
在△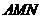 中,
中, 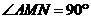 ,
,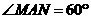
∴
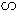
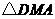 ··············· (3分)
··············· (3分)
(2)证明 :如图甲,作
:如图甲,作 //
//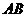 交
交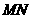 于点
于点 ,则
,则


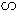

∴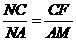
又 ≌
≌
∴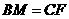
∴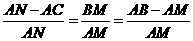
∴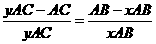
即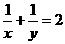 ····················· (3分)
····················· (3分)

(3)①如图乙,过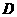 作
作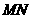 ∥
∥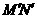 交
交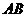 于
于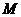 ,交
,交 的延长线于
的延长线于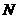 ,则
,则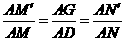
∴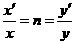 ,
,
 即
即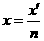 ,
,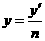
由(2)知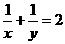
∴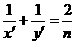
②如图丙,当过点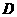 作
作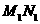 ∥
∥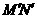 交
交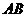 的延长线于
的延长线于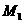 ,交
,交 1于
1于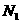 ,则同理可得
,则同理可得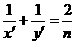
·························· (3分)
25.(10分)解:(1)由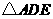 ≌
≌  得
得
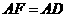
又由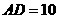 ,
,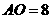
∴ ,
,
∴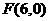 ····················· (3分)
····················· (3分)
(2)依题意可设过点 、
、 的抛物线解析式为
的抛物线解析式为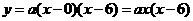
依题意知,抛物线与直线 相切,
相切,
即由 得
得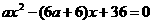 有两个相等的实数根
有两个相等的实数根
∴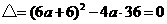 ,得
,得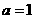
∴抛物线的解析式为 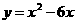 ··········· (3分)
··········· (3分)
(3)设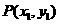 ,
, 假设
假设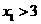 ,
, 依题意得
依题意得
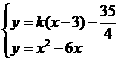 得
得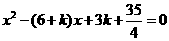
∴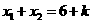 ,
, ·········· (2分)
·········· (2分)
又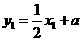 ,
,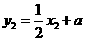
∵

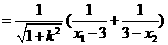

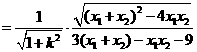 即
即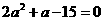
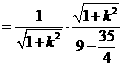
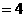 为定值··········· (2分)
为定值··········· (2分)