一、选择题

1、下列各数中是无理数的是

Ａ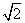．　Ｂ．-2 　Ｃ．0　Ｄ．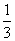

2、下列计算正确的是

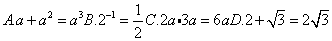
3、如图，AB是池塘两端，设计一方法测量AB的距离，取点C，连接AC、BC，再取它们的中点D、E，测得DE=15米，则AB=

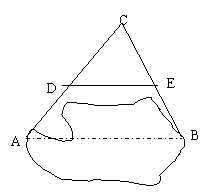
Ａ．7.5，Ｂ．15，Ｃ．22.5，Ｄ． 30

4、分式方程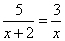的解为

Ａ．1,Ｂ．2,Ｃ．3,Ｄ．4

5、如图，所给三视图的几何体是：

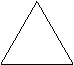
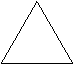
主视图 左视图 俯视图

Ａ．球，Ｂ．圆柱，Ｃ．圆锥，Ｄ．三棱锥

6、若式子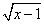有意义，则ｘ的取值范围是：

Ａ．ｘ＞１Ｂ≥１Ｃ．ｘ＜１Ｄ．ｘ≤１

７、以下四个命题正确的是

A.任意三点可以确定一个圆

B.菱形对角线相等

C.直角三角形斜边上的中线等于斜边的一半

D.平行四边形的四条边相等

8、如图，A、B两点在双曲线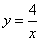上，分别经过A、B两点向轴作垂线段，已知S阴影=1，则S1+S2=

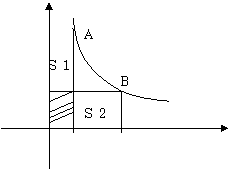
Ａ．３Ｂ．４Ｃ．５Ｄ．６

二、填空题

9、-3的相反数是______

10、因式分解：ax-a=_____________

11、未测试两种电子表的走时误差，做了如下统计

	平均数	方差
甲	0.4	0.026
乙	0.4	0.137

则这两种电子表走时稳定的是________

12、计算：__________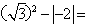

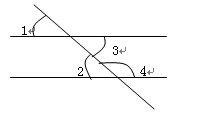
13、如图，直线a、b被直线c所截，若满足__________________________，则a、c平行。

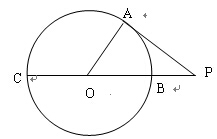
14、如图，O的半径为3，P是CB延长线上一点，PO=5，PA切O于A点，则PA=______

15、七、八年级学生分别到雷锋、毛泽东纪念馆参观，共589人，到毛泽东纪念馆的人数是到雷锋纪念馆人数的2倍56人，设七年级为x人，可列方程为_______________________

16、如图：

1

2 3 4

3 4 5 6 7

4 5 6 7 8 9 10

……

按此规律，第6行最后一个数字是_______，第_____行最后一个数是2014.

_ueditor_page_break_tag_

三、综合解答题

17、在边长为1的小正方形网格中，⊿AOB的顶点均在格点上，

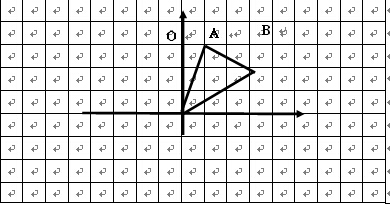
(1)B点关于y轴的对称点坐标为______________

(2)将⊿AOB向左平移3个单位长度得到⊿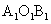，请画出⊿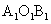

（3）在（2）的条件下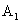，的坐标为___________

18、先化简，在求值

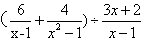，其中x=2

19、如图，修公路遇到一座山，于是要修一条隧道。为了加快施工进度，想在小山的另一侧同时施工。为了使山的另一侧的开挖点C在AB的延长线上，设想过C点作直线AB的垂线L，过点B作一直线（在山的旁边经过），与L相交于D点，经测量∠ABD=135o，BD=800米，求直线L上距离D点多远的C处开挖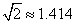？（，精确到1米）

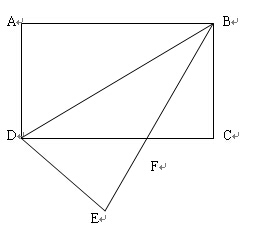
20、如图，将矩形ABCD沿BD对折，点A落在E处，BE与CD相交于F，若AD=3，BD=6。

（1）求证：≌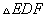

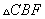
（2）求∠EBC

21、某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共8台，具体情况如下表：

	A型	B型
价格（万元/台）	12	10
月污水处理能力（吨/月）	200	160

经预算，企业最多支出89万元购买设备，且要求月处理污水能力不低于1380吨。

（1）该企业有几种购买方案

（2）哪种方案更省钱，说明理由

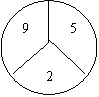
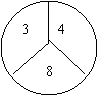
22、有两个构造完全相同（除所标数字外）的转盘A、B，游戏规定，转动两个转盘各一次，指向大的数字获胜。现由你和小明各选择一个转盘游戏，你会选择哪一个，为什么？

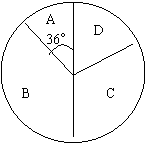
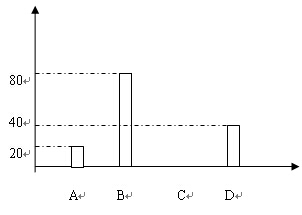
23、从全校1200名学生中随机选取一部分学生进行调查，调查情况：A、上网时间≤1小时；B、1小时<上网时间≤4小时；C、4小时<上网时间≤7小时；D、上网时间>7小时。统计结果制成了如下统计图：

（1）参加调查的学生有______人

（2）请将条形统计图补全

（3）请估计全校上网不超过7小时的学生人数

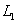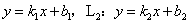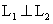24、已知两直线：，若，则有。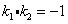

（1）应用：已知Y=2x+1与Y=kx-1垂直，求 k

(2)直线经过A（2,3），且与Y=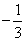x+3垂直，求解析式

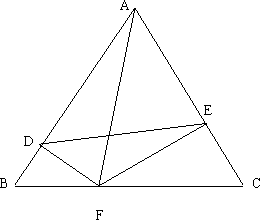
25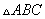．为等边三角形，变长为a，，

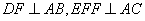（1）求证：⊿BDF∽⊿CEF

（2）若a=4，设BF=m，四边形ADFE面积为S，求出S与m之间的函数关系，并探究当m为何值时S取最大值；

（3）已知A、D、F、E四点共圆，已知tan∠EDF=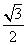，求此圆直径。

26．已知二次函数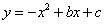的对称轴为x=2，且经过原点，直线AC解析式为y=kx+4，

（1）求二次函数解析式

（2）若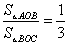，求K

（3）若以ＢＣ为直径的圆经过原点，求Ｋ