一、选择题（本大题共8小题，每小题3分，满分24分，在每小题给出的四个选项中，只有一项是符合题目要求的．）

1．（3分）（2014•锦州）﹣1.5的绝对值是（　　）

A． 0 B． ﹣1.5 C． 1.5 D．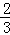

考点： 绝对值

分析： 计算绝对值要根据绝对值的定义求解．第一步列出绝对值的表达式；第二步根据绝对值定义去掉这个绝对值的符号．

解答： 解：|﹣1.5|=1.5．

故选：C．

点评： 此题考查了绝对值的性质，要求掌握绝对值的性质及其定义，并能熟练运用到实际运算当中．绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．

2．（3分）（2014•锦州）如图，在一水平面上摆放两个几何体，它的主视图是（　　）

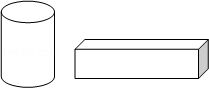
A． B． C． D．

考点： 简单组合体的三视图．.

分析： 找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．

解答： 解：从正面看易得左边是一个竖着的长方形，右边是一个横着的长方形，

故选：B．

点评： 本题考查了三视图的知识，主视图是从物体的正面看得到的视图．

3．（3分）（2014•锦州）下列计算正确的是（　　）

A． 3x+3y=6xy B． a2•a3=a6 C． b6÷b3=b2 D． （m2）3=m6

考点： 同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．.

分析： 根据合并同类项的法则，同底数幂的乘法与除法以及幂的乘方的知识求解即可求得答案．

解答： A、3x与3y不是同类项，不能合并，故A选项错误；

B、a2•a3=a5，故B选项错误；

C、b6÷b3=b3 ，故C选项错误；

D、（m2）3=m6 ，故D选项正确．

故选：D．

点评： 此题考查了合并同类项的法则，同底数幂的乘法与除法以及幂的乘方等知识，解题要注意细心．

4．（3分）（2014•锦州）已知a＞b＞0，下列结论错误的是（　　）

A． a+m＞b+m B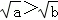． C． ﹣2a＞﹣2b D．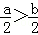

考点： 不等式的性质．.

分析： 运用不等式的基本性质判定即可．

解答： 解：a＞b＞0，

A、a+m＞b+m，故A选项正确；

B、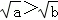，故B选项正确；

C、﹣2a＜﹣2b，故C选项错误；

D、＞，故D选项正确．

故选：C．

点评： 本题主要考查了不等式的基本性质，熟记不等式的基本性质是解题的关键．

5．（3分）（2014•锦州）如图，直线a∥b，射线DC与直线a相交于点C，过点D作DE⊥b于点E，已知∠1=25°，则∠2的度数为（　　）

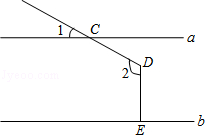
A． 115° B． 125° C． 155° D． 165°

考点： 平行线的性质．.

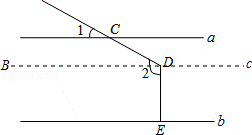
分析： 如图，过点D作c∥a．由平行线的性质进行解题．

解答： 解：如图，过点D作c∥a．

则∠1=∠CDB=25°．

又a∥b，DE⊥b，

∴b∥c，DE⊥c，

∴∠2=∠CDB+90°=115°．

故选：A．

点评： 本题考查了平行线的性质．此题利用了“两直线平行，同位角相等”来解题的．

6．（3分）（2014•锦州）某销售公司有营销人员15人，销售部为了制定某种商品的月销售量定额，统计了这15人某月的销售量，如下表所示：

那么这15位销售人员该月销售量的平均数、众数、中位数分别是（　　）

A． 320，210，230 B． 320，210，210 C． 206，210，210 D． 206，210，230

考点： 加权平均数；中位数；众数．.

分析： 找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数，众数是一组数据中出现次数最多的数据，注意众数可以不止一个．平均数是指在一组数据中所有数据之和再除以数据的个数．

解答： 解：平均数是：（1800+510+250×3+210×5+150×3+120×2）÷15=4800÷15=320（件）；

210出现了5次最多，所以众数是210；

表中的数据是按从大到小的顺序排列的，处于中间位置的是210，因而中位数是210（件）．

故选B．

点评： 此题主要考查了一组数据平均数的求法，以及众数与中位数的求法，又结合了实际问题，此题比较典型．

7．（3分）（2014•锦州）二次函数y=ax2+bx+c（a≠0，a，b，c为常数）的图象如图，ax2+bx+c=m有实数根的条件是（　　）

A． m≥﹣2 B． m≥5 C． m≥0 D． m＞4

考点： 抛物线与x轴的交点．.

分析： 根据题意利用图象直接得出m的取值范围即可．

解答： 解：一元二次方程ax2+bx+c=m有实数根，

可以理解为y=ax2+bx+c和y=m有交点，

可见，m≥﹣2，

故选：A．

点评： 此题主要考查了利用图象观察方程的解，正确利用数形结合得出是解题关键．

8．（3分）（2014•锦州）哥哥与弟弟的年龄和是18岁，弟弟对哥哥说：“当我的年龄是你现在年龄的时候，你就是18岁”．如果现在弟弟的年龄是x岁，哥哥的年龄是y岁，下列方程组正确的是（　　）

考点： 由实际问题抽象出二元一次方程组．.

分析： 由弟弟的年龄是x岁，哥哥的年龄是y岁，根据“哥哥与弟弟的年龄和是18岁，”，哥哥与弟弟的年龄差不变得出18﹣y=y﹣x，列出方程组即可．

解答： 解：设现在弟弟的年龄是x岁，哥哥的年龄是y岁，由题意得

．

故选：D．

点评： 此题考查由实际问题列方程组，注意找出题目蕴含的数量关系解决问题．

二、填空题（本大题共8小题，每小题3分，满分24分.）

9．（3分）（2014•锦州）分解因式2x2﹣4x+2的最终结果是　2（x﹣1）2　．

考点： 提公因式法与公式法的综合运用．.

分析： 先提取公因式2，再对余下的多项式利用完全平方公式继续分解．

解答： 解：2x2﹣4x+2，

=2（x2﹣2x+1），

=2（x﹣1）2．

故答案为：2（x﹣1）2．

点评： 本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．

10．（3分）（2014•锦州）纳米是一种长度单位，它用来表示微小的长度，1纳米微10亿分之一米，即1纳米=10﹣9米，1根头发丝直径是60000纳米，则一根头发丝的直径用科学记数法表示为　6×10﹣5　米．

考点： 科学记数法—表示较小的数．.

分析： 绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

解答： 解：60000纳米=60000×10﹣9米=0.000 06米=6×10﹣5米；

故答案为：6×10﹣5．

点评： 本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．

11．（3分）（2014•锦州）计算：tan45°﹣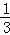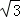（﹣1）0=　　．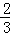

考点： 实数的运算；零指数幂；特殊角的三角函数值．

专题： 计算题．

分析： 原式第一项利用特殊角的三角函数值计算，第二项利用零指数幂法则计算即可得到结果．

解答： 解：原式=1﹣=．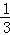

故答案为：

点评： 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

12．（3分）（2014•锦州）方程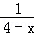﹣=1的解是　x=0　．

考点： 解分式方程．

专题： 计算题．

分析： 分式方程变形后，去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

解答： 解：去分母得：﹣1﹣3﹣x=x﹣4，

移项合并得：2x=0，

解得：x=0，

经检验x=0是分式方程的解，

故答案为：x=0

点评： 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．

13．（3分）（2014•锦州）如图，在一张正方形纸片上剪下一个半径为r的圆形和一个半径为R的扇形，使之恰好围成图中所示的圆锥，则R与r之间的关系是　R=4r　．

考点： 圆锥的计算．.

分析： 利用圆锥的底面周长等于侧面展开图的扇形弧长，根据弧长公式计算．

解答： 解：扇形的弧长是：=，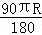

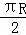圆的半径为r，则底面圆的周长是2πr，

圆锥的底面周长等于侧面展开图的扇形弧长则得到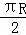：=2πr，

∴=2r，

即：R=4r，

r与R之间的关系是R=4r．

故答案为：R=4r．

点评： 本题综合考查有关扇形和圆锥的相关计算．解题思路：解决此类问题时要紧紧抓住两者之间的两个对应关系：（1）圆锥的母线长等于侧面展开图的扇形半径；（2）圆锥的底面周长等于侧面展开图的扇形弧长．正确对这两个关系的记忆是解题的关键．

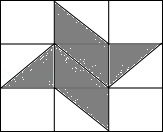
14．（3分）（2014•锦州）某数学活动小组自制一个飞镖游戏盘，如图，若向游戏盘内投掷飞镖，投掷在阴影区域的概率是　　．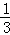

考点： 几何概率

分析： 利用阴影部分面积除以总面积=投掷在阴影区域的概率，进而得出答案．

解答： 解：由题意可得，投掷在阴影区域的概率是：=．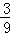

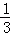故答案为：．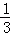

点评： 此题主要考查了几何概率，求出阴影部分面积与总面积的比值是解题关键．

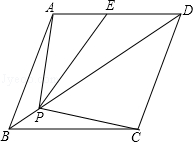
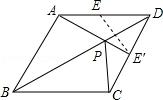
15．（3分）（2014•锦州）菱形ABCD的边长为2，∠ABC=60°，E是AD边中点，点P是对角线BD上的动点，当AP+PE的值最小时，PC的长是　　．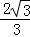

考点： 轴对称-最短路线问题；菱形的性质．.

分析： 作点E关于直线BD的对称点E′，连接AE′，则线段AE′的长即为AP+PE的最小值，再由轴对称的性质可知DE=DE′=1，故可得出△AE′D是直角三角形，由菱形的性质可知∠PDE′=∠ADC=30°，根据锐角三角函数的定义求出PE的长，进而可得出PC的长．

解答： 解：如图所示，

作点E关于直线BD的对称点E′，连接AE′，则线段AE′的长即为AP+PE的最小值，

∵菱形ABCD的边长为2，E是AD边中点，

∴DE=DE′=AD=1，

∴△AE′D是直角三角形，

∵∠ABC=60°，

∴∠PDE′=∠ADC=30°，

∴PE′=DE′•tan30°=，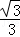

∴PC===．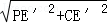

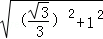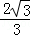故答案为：．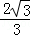

点评： 本题考查的是轴对称﹣最短路线问题，熟知菱形的性质及锐角三角函数的定义是解答此题的关键．

16．（3分）（2014•锦州）如图，点B1在反比例函数y=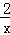（x＞0）的图象上，过点B1分别作x轴和y轴的垂线，垂足为C1和A，点C1的坐标为（1，0）取x轴上一点C2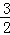（，0），过点C2分别作x轴的垂线交反比例函数图象于点B2，过B2作线段B1C1的垂线交B1C1于点A1，依次在x轴上取点C3（2，0），C4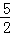（，0）…按此规律作矩形，则第n（ n≥2，n为整数）个矩形）An﹣1Cn﹣1CnBn的面积为　　．

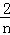考点： 反比例函数系数k的几何意义．

专题： 规律型．

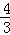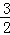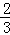分析： 根据反比例函数的比例系数k的几何意义得到第1个矩形的面积=2，第2个矩形的面积=×（﹣1）=，第3个矩形的面积=（2﹣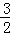）×1=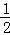，…于是得到第n个矩形的面积=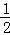×=，由此得出答案即可．

解答： 解：第1个矩形的面积=2，

第2个矩形的面积=×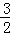（﹣1）=，

第3个矩形的面积=（2﹣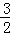）×1=，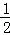

…

第n个矩形的面积=×=．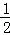

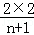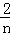故答案为：．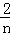

点评： 本题考查了反比例函数的比例系数k的几何意义：在反比例函数y=图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．

三、解答题（本大题共10小题，满分102分，解答应写出文字说明、证明过程或演算步骤）

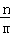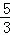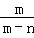17．（8分）（2014•锦州）已知=，求式子（﹣）÷的值．

考点： 分式的化简求值．

分析： 先根据分式混合运算的法则把原式进行化简，再根据=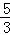得出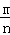=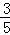，代入原式进行计算即可．

解答： 解：原式=•

=

=

=，

∵=，

∴=，

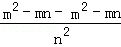
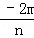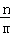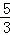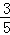∴原式=﹣2×=﹣．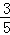

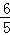点评： 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

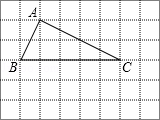
18．（8分）（2014•锦州）如图，在边长为1个单位长度的小正方形组成的网格中，按要求作图．

（1）利用尺规作图在AC边上找一点D，使点D到AB、BC的距离相等．（不写作法，保留作图痕迹）

（2）在网格中，△ABC的下方，直接画出△EBC，使△EBC与△ABC全等．

考点： 作图—复杂作图；全等三角形的判定；角平分线的性质．.

分析： （1）作∠ABC的平分线即可；

（2）利用点A关于BC的对称点E画出△EBC．

解答： 解：（1）如图，作∠ABC的平分线，

（2）如图，

点评： 本题主要考查了作图﹣复杂作图，角平分线的性质及全等三角形的判定，解题的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图．

19．（8分）（2014•锦州）对某市中学生的幸福指数进行调查，从中抽取部分学生的调查表问卷进行统计，并绘制出不完整的统计表和条形统计图．

（1）直接补全统计表．

（2）补全条形统计图（不要求写出计算过程）．

（3）抽查的学生约占全市中学生的5%，估计全市约有多少名中学生的幸福指数能达到五★级？

考点： 条形统计图；用样本估计总体；频数（率）分布表．.

分析： （1）根据统计图中，4颗星的人数是300人，占0.3；根据频数与频率的关系，可知共随机调查的总人数，根据总人数即可求出别的数据．

（2）根据（1）中求出的数值，据此可补全条形图；

（3）先求出全市中学生的总人数，再除以对应的幸福指数为5颗星的百分比．

解答： 解：（1）对中学生的幸福指数进行调查的人数：300÷0.30=1000（人）

一颗星的频率为：60÷1000=0.06，

二颗星的频率为：80÷1000=0.08，

三颗星的频数为：1000×0.16=160，

四颗星的频数为：300，

五颗星的频数为：1000﹣60﹣80﹣160﹣300=400，

五颗星的频率为：400÷1000=0.40．

故答案为：0.06，0.08，160，300，400，0.40．

（2）如图，根据（1）中求出的数值，据此可补全条形图；

（3）1000÷5%×0.4=8000（名）

答：估计全市约有8000名中学生的幸福指数能达到五★级．

点评： 本题考查的是条形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．用到的知识点为：总体数目=部分数目÷相应百分比．

20．（10分）（2014•锦州）某学校游戏节活动中，设计了一个有奖转盘游戏，如图，A转盘被分成三个面积相等的扇形，B转盘被分成四个面积相等的扇形，每一个扇形都标有相应的数字，先转动A转盘，记下指针所指区域内的数字，再转动B转发盘，记下指针所指区域内的数字（当指针在边界线上时，重新转动一次，直到指针指向一下区域内为止），然后，将两次记录的数据相乘．

（1）请利用画树状图或列表格的方法，求出乘积结果为负数的概率．

（2）如果乘积是无理数时获得一等奖，那么获得一等奖的概率是多少？

考点： 列表法与树状图法．

专题： 计算题．

分析： （1）列表得出所有等可能的情况数，找出乘积为负数的情况数，即可求出所求的概率；

（2）找出乘积为无理数的情况数，即可求出一等奖的概率．

解答： 解：列表如下：

1.5 ﹣3 ﹣

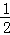
0 0 0 0 0

1 1.5 ﹣3 ﹣

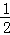
﹣1 ﹣1.5 3 ﹣

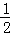
所有等可能的情况有12种，

（1）乘积结果为负数的情况有4种，

则P（乘积结果为负数）==；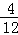

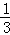（2）乘积是无理数的情况有2种，

则P（乘积为无理数）==．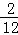

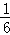点评： 此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．

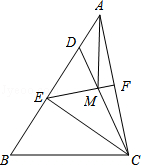
21．（10分）（2014•锦州）如图，在△ABC中，点D在AB上，且CD=CB，点E为BD的中点，点F为AC的中点，连结EF交CD于点M，连接AM．

（1）求证：EF=AC．

（2）若∠BAC=45°，求线段AM、DM、BC之间的数量关系．

考点： 直角三角形斜边上的中线；等腰三角形的判定与性质；等腰直角三角形．.

分析： （1）根据等腰三角形三线合一的性质可得CE⊥BD，再根据直角三角形斜边上的中线等于斜边的一半可得EF=AC；

（2）判断出△AEC是等腰直角三角形，根据等腰直角三角形的性质可得EF垂直平分AC，再根据线段垂直平分线上的点到两端点的距离相等可得AM=CM，然后求出CD=AM+DM，再等量代换即可得解．

解答： （1）证明：∵CD=CB，点E为BD的中点，

∴CE⊥BD，

∵点F为AC的中点，

∴EF=AC；

（2）解：∵∠BAC=45°，CE⊥BD，

∴△AEC是等腰直角三角形，

∵点F为AC的中点，

∴EF垂直平分AC，

∴AM=CM，

∵CD=CM+DM=AM+CM，CD=CB，

∴BC=AM+DM．

点评： 本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形的性质等腰直角三角形的判定与性质，难点在于（2）判断出EF垂直平分AC．

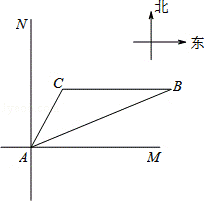
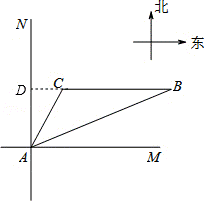
22．（10分）（2014•锦州）如图，位于A处的海上救援中心获悉：在其北偏东68°方向的B处有一艘渔船遇险，在原地等待营救．该中心立即把消息告知在其北偏东30°相距20海里的C处救生船，并通知救生船，遇险船在它的正东方向B处，现救生船沿着航线CB前往B处救援，若救生船的速度为20海里/时，请问：救生船到达B处大约需要多长时间？（结果精确到0.1小时：参考数据：sin38°≈0.62，cos38°≈0.79，sin22°≈0.37，cos22°≈0.93，sin37°≈0.60，cos37°≈0.80）

考点： 解直角三角形的应用-方向角问题．.

分析： 延长BC交AN于点D，则BC⊥AN于D．先解Rt△ACD，求出CD=AC=10，AD=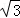CD=10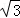，再解Rt△ABD，得到∠B=22°，AB=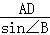≈46.81，BD=AB•cos∠B≈43.53，则BC=BD﹣CD≈33.53，然后根据时间=路程÷速度即可求出救生船到达B处大约需要的时间．

解答： 解：如图，延长BC交AN于点D，则BC⊥AN于D．

在Rt△ACD中，∵∠ADC=90°，∠DAC=30°，

∴CD=AC=10，AD=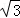CD=10．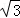

在Rt△ABD中，∵∠ADB=90°，∠DAB=68°，

∴∠B=22°，

∴AB=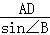≈≈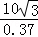46.81，

BD=AB•cos∠B≈46.81×0.93=43.53，

∴BC=BD﹣CD≈43.53﹣10=33.53，

∴救生船到达B处大约需要：33.53÷20≈1.7（小时）．

答：救生船到达B处大约需要1.7小时．

点评： 本题考查了解直角三角形的应用﹣方向角问题，准确作出辅助线构造直角三角形，进而求出BC的长度是解题的关键．

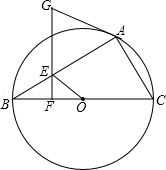
23．（10分）（2014•锦州）如图，已知，⊙O为△ABC的外接圆，BC为直径，点E在AB上，过点E作EF⊥BC，点G在FE的延长线上，且GA=GE．

（1）求证：AG与⊙O相切．

（2）若AC=6，AB=8，BE=3，求线段OE的长．

考点： 切线的判定．.

分析： （1）连接OA，由OA=OB，GA=GE得出∠ABO=∠BAO，∠GEA=∠GAE；再由EF⊥BC，得出∠BFE=90°，进一步由∠ABO+∠BEF=90°，∠BEF=∠GEA，最后得出∠GAO=90°求得答案；

（2）BC为直径得出∠BAC=90°，利用勾股定理得出BC=10，由△BEF∽△BCA，求得EF、BF的长，进一步在△OEF中利用勾股定理得出OE的长即可．

解答： （1）证明：如图，

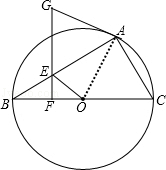
连接OA，

∵OA=OB，GA=GE

∴∠ABO=∠BAO，∠GEA=∠GAE

∵EF⊥BC，

∴∠BFE=90°，

∴∠ABO+∠BEF=90°，

又∵∠BEF=∠GEA，

∴∠GAE=∠BEF，

∴∠BAO+∠GAE=90°，

即AG与⊙O相切．

（2）解：∵BC为直径，

∴∠BAC=90°，AC=6，AB=8，

∴BC=10，

∵∠EBF=∠CBA，∠BFE=∠BAC，

∴△BEF∽△BCA，

∴==

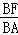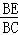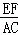
∴EF=1.8，BF=2.4，

∴0F=0B﹣BF=5﹣2.4=2.6，

∴OE==．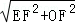

点评： 本题考查了切线的判定：过半径的外端点与半径垂直的直线是圆的切线．也考查了勾股定理、相似三角形的判定与性质以及圆周角定理的推论．

24．（12分）（2014•锦州）在机器调试过程中，生产甲、乙两种产品的效率分别为y1、y2（单位：件/时），y1、y2与工作时间x（小时）之间大致满足如图所示的函数关系，y1的图象为折线OABC，y2的图象是过O、B、C三点的抛物线一部分．

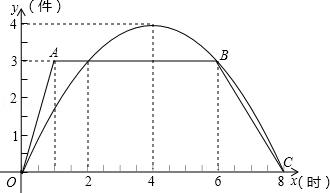
（1）根据图象回答：调试过程中，生产乙的效率高于甲的效率的时间x（小时）的取值范围是　2＜x＜6　；‚说明线段AB的实际意义是　从第二小时到第六小时甲的工作效率是3件　．

（2）求出调试过程中，当6≤x≤8（3）时，生产甲种产品的效率y1（件/时）与工作时间x（小时）之间的函数关系式．

（3）调试结束后，一台机器先以图中甲的最大效率生产甲产品m小时，再以图中乙的最大效率生产乙产品，两种产品共生产6小时，求甲、乙两种产品的生产总量Z（件）与生产甲所用时间m（小时）之间的函数关系式．

考点： 二次函数的应用．.

分析： （1）根据y2图象在y1上方的部分，可得答案，根据线段AB的工作效率没变，可得答案案；

（2）根据待定系数法，可得函数解析式；

（3）根据根据甲的最大效率乘以时间，可得甲的产品，根据乙的最大效率乘以乙的时间，可得乙的产品，甲的产品加乙的产品，可得答案．

解答： 解：（1）y2图象在y1上方的部分，生产乙的效率高于甲的效率的时间x（小时）的取值范围是 2＜x＜6；

‚线段AB的实际意义是 从第二小时到第六小时甲的工作效率是3件；

（2）设函数解析式是y1=kx+b，

图象过点B（6，3）、C（8，0）

，

解得，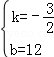

故函数解析式为y1=﹣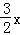+12；

（3）Z=3m+4（6﹣m），

即Z=﹣m+24．

点评： 本题考查了二次函数的应用，利用了函数图象，待定系数法，题目较为简单．

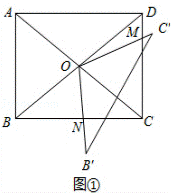
25．（12分）（2014•锦州）（1）已知正方形ABCD中，对角线AC与BD相交于点O，如图①，将△BOC绕点O逆时针方向旋转得到△B′OC′，OC′与CD交于点M，OB′与BC交于点N，请猜想线段CM与BN的数量关系，并证明你的猜想．

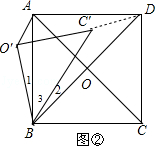
（2）如图②‚，将（1）中的△BOC绕点B逆时针旋转得到△BO′C′，连接AO′、DC′，请猜想线段AO′与DC′的数量关系，并证明你的猜想．

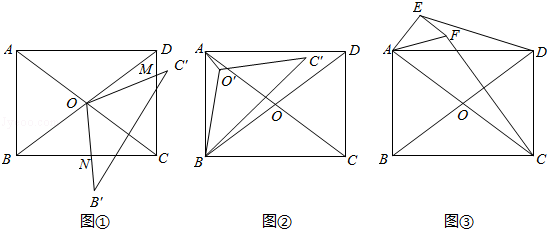
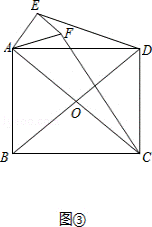
（3）如图③ƒ，已知矩形ABCD和Rt△AEF有公共点A，且∠AEF=90°，∠EAF=∠DAC=α，连接DE、CF，请求出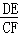的值（用α的三角函数表示）．

考点： 四边形综合题．.

专题： 综合题．

分析： （1）如图1①，根据正方形的性质得OB=OC，∠OBC=∠OCD=45°，∠BOC=90°，再根据旋转的性质得∠B′OC′=∠BOC=90°，然后利用等角的余角相等得∠B′OB′=∠COC′，则可根据“ASA”判断△BON≌△COM，于是得到CM=BN；

（2）如图②，连接DC′，根据正方形的性质得AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，于是可判断△ABC和△OBC都是等腰直角三角形，

则AC=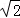AB，BC=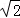BO，所以BD=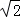AB；再根据旋转的性质得∠O′BC′=∠OBC=45°，OB=O′B，BC′=BC，则BC′=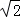BO′，所以==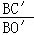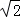，再证明∠1=∠2，则可根据相似的判定定理得到△BDC′∽△BAO′，利用相似比即可得到DC′=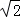AO′；

（3）如图③，根据余弦的定义，在Rt△AEF中得到cos∠EAF=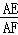；在Rt△DAC中得到cos∠DAC=，由于∠EAF=∠DAC=α，所以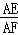==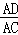cosα，∠EAD=∠FAC，则可根据相似的判定定理得到△AED∽△AFC，利用相似比即可得到=cosα．

解答： 解：（1）CM=BN．理由如下：如图①，

∵四边形ABCD为正方形，

∴OB=OC，∠OBC=∠OCD=45°，∠BOC=90°，

∵△BOC绕点O逆时针方向旋转得到△B′OC′，

∴∠B′OC′=∠BOC=90°，

∴∠B′OC+∠COC′=90°，

而∠BOB′+∠B′OC=90°，

∴∠B′OB′=∠COC′，

在△BON和△COM中

，

∴△BON≌△COM，

∴CM=BN；

（2）如图②，连接DC′，

∵四边形ABCD为正方形，

∴AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，

∴△ABC和△OBC都是等腰直角三角形，

∴AC=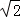AB，BC=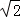BO，

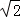∴BD=AB，

∵△BOC绕点B逆时针方向旋转得到△B′OC′，

∴∠O′BC′=∠OBC=45°，OB=O′B，BC′=BC，

∴BC′=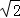BO′，

∴==，

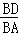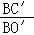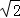∵∠1+∠3=45°，∠2+∠3=45°，

∴∠1=∠2，

∴△BDC′∽△BAO′，

∴==，

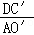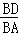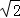∴DC′=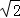AO′；

（3）如图③，在Rt△AEF中，cos∠EAF=；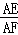

在Rt△DAC中，cos∠DAC=，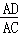

∵∠EAF=∠DAC=α，

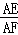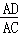∴==cosα，∠EAF+∠FAD=∠FAD+∠DAC，即∠EAD=∠FAC，

∴△AED∽△AFC，

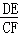∴==cosα．

点评： 本题考查了四边形的综合题：熟练掌握矩形和正方形的性质；同时会运用等腰直角三角形的性质和旋转的性质；能灵活利用三角形全等或相似的判定与性质解决线段之间的关系．

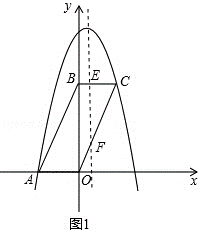
26．（14分）（2014•锦州）如图，平行四边形ABCD在平面直角坐标系中，点A的坐标为（﹣2，0），点B的坐标为（0，4），抛物线y=﹣x2+mx+n经过点A和C．

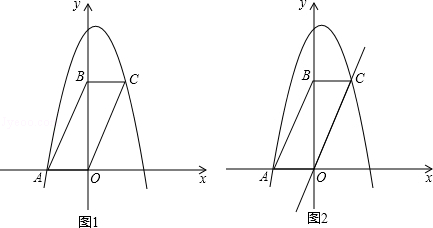
（1）求抛物线的解析式．

（2）该抛物线的对称轴将平行四边形ABCO分成两部分，对称轴左侧部分的图形面积记为S1，右侧部分图形的面积记为S2，求S1与S2的比．

（3）在y轴上取一点D，坐标是（0，），将直线OC沿x轴平移到O′C′，点D关于直线O′C′的对称点记为D′，当点D′正好在抛物线上时，求出此时点D′坐标并直接写出直线O′C′的函数解析式．

考点： 二次函数综合题；待定系数法求一次函数解析式；待定系数法求二次函数解析式；平行四边形的性质；锐角三角函数的定义．.

专题： 综合题．

分析： （1）由条件可求出点C的坐标，然后用待定系数法就可求出抛物线的解析式．

（2）由抛物线的解析式可求出其对称轴，就可求出S2，从而求出S1，就可求出S1与S2的比．

（3）由题可知DD′⊥O′C′，且DD′的中点在直线O′C′上．由OC∥O′C′可得DD′⊥OC．过点D作DM⊥CO，交x轴于点M，只需先求出直线DM的解析式，再求出直线DM与抛物线的交点，就得到点D′的坐标，然后求出DD′中点坐标就可求出对应的直线O′A′的解析式．

解答： 解：（1）如图1，

∵四边形ABCO是平行四边形，

∴BC=OA，BC∥OA．

∵A的坐标为（﹣2，0），点B的坐标为（0，4），

∴点C的坐标为（2，4）．

∵抛物线y=﹣x2+mx+n经过点A和C．

∴．

解得：．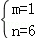

∴抛物线的解析式为y=﹣x2+x+6．

（2）如图1，

∵抛物线的解析式为y=﹣x2+x+6．

∴对称轴x=﹣=，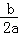

设OC所在直线的解析式为y=ax，

∵点C的坐标为（2，4），

∴2a=4，即a=2．

∴OC所在直线的解析式为y=2x．

当x=时，y=1，则点F为（，1）．

∴S2=EC•EF

=×（2﹣）×（4﹣1）=．

∴S1=S四边形ABCO﹣S2=2×4﹣=．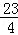

∴S1：S2=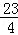： =23：9．

∴S1与S2的比为23：9．

（3）过点D作DM⊥CO，交x轴于点M，如图2，

∵点C的坐标为（2，4），

∴tan∠BOC=．

∵∠OMD=90°﹣∠MOC=∠BOC，

∴tan∠OMD==．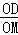

∵点D的坐标是（0，），

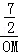∴=，即OM=7．

∴点M的坐标为（7，0）．

设直线DM的解析式为y=kx+b，

则有，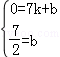

解得：

∴直线DM的解析式为y=﹣x+．

∵点D与点D′关于直线O′C′对称，

∴DD′⊥O′C′，且DD′的中点在直线O′C′上．

∵OC∥O′C′，∴DD′⊥OC．

∴点D′是直线DM与抛物线的交点．

联立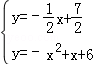

解得：，，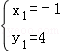

∴点D′的坐标为（﹣1，4）或（，）．

设直线O′C′的解析式为y=2x+c，

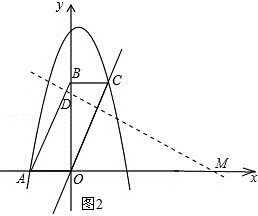
①当点D′的坐标为（﹣1，4）时，如图3，

线段DD′的中点为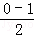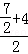（，）即（﹣，），

则有2×（﹣）+c=，

解得：c=．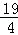

此时直线O′C′的解析式为y=2x+．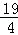

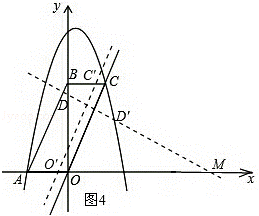
②当点D′的坐标为（，）时，如图4，

同理可得：此时直线O′C′的解析式为y=2x+．

综上所述：当点D′的坐标为（﹣1，4）时，直线O′C′的解析式为y=2x+；当点D′的坐标为（，）时，直线O′C′的解析式为y=2x+．

点评： 本题考查了用待定系数法求二次函数及一次函数的解析式、抛物线与直线的交点、平行四边形的性质、三角函数的定义、中点坐标公式等知识，有一定的综合性．