(单词翻译:单击)
试卷真题1
卷Ⅰ(选择题)
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中唯一的正确选项,不选多选、错选,均不得分)
1.-3的绝对值为( )
(A)-3 (B)3 (C)  (D)
(D) 
2.一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9.这5个数据的中位数是( )
(A)6 (B)7 (C)8 (D)9
3.2013年12月15日,我国“玉兔号”月球车顺利抵达月球表面.月球离地球平均距离是384 400 000米,数据38 4 400 000用科学记数法表示为( )
4 400 000用科学记数法表示为( )
(A)3.844×108 (B)3.844×107 (C)3.844×106 (D)38.44×106
4.小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
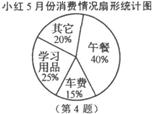
(A)各项消费金额占消费总金额的百分比
(B)各项消费的金额
(C)消费的总金额
(D)各项消费金额的增减变化情况
5.如图,⊙0的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( )
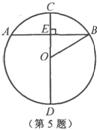
(A)2 (B)4 (C)6 (D)8
6.下列运算正确的是( )
(A) 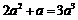 (B)
(B) 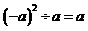
(C) 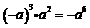 (D)
(D) 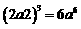
7.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
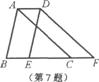
(A)16cm (B)18cm (C)20cm (D)22cm
8.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )
(A)1.5 (B)2 (C)2.5 (D)3
9.如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
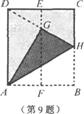
(A)2cm (B) 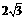 cm (C)4cm (D)
cm (C)4cm (D) 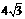 cm
cm
10.当-2≤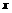 ≤l时。二次函数
≤l时。二次函数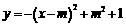 有最大值4,则实数m的值为( )
有最大值4,则实数m的值为( )
(A) 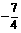 (B)
(B) 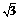 或
或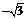 (c)2或
(c)2或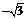 (D)2或
(D)2或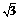 或
或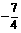
卷Ⅱ(非选择题)
二、填空题(本题有6小题,每小题4分,共24分)
11.方程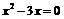 的根为_______________.
的根为_______________.
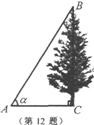
12.如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为____________米(用含α的代数式表示).
13.有三辆车 按1,2,3编号,舟舟和
按1,2,3编号,舟舟和 嘉嘉两人可任意选坐一辆车.则两人同坐3号车的概率
嘉嘉两人可任意选坐一辆车.则两人同坐3号车的概率 为____________.
为____________.
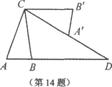
14.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB,CA′相交于点D,则线段B D的长为____________.
D的长为____________.
15.过点(-1,7)的一条直线与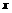 轴,y轴分别相交于点A,B,且与直线
轴,y轴分别相交于点A,B,且与直线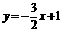 平行.则在线段AB上,横、纵坐标都是整数的点的坐标是 ____________ .
平行.则在线段AB上,横、纵坐标都是整数的点的坐标是 ____________ .
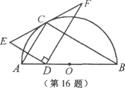
16.如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与 点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为
点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为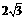 ;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=
;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=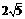 ;⑤当点D从点A运动到点B时,线段EF扫过的面积是
;⑤当点D从点A运动到点B时,线段EF扫过的面积是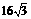 .其中正确结论的序号是____________.
.其中正确结论的序号是____________.
试卷真题2
三、解答题(本题有8小题,第17~19题每小题6分,第20,21题每小题8分,第22,23题每小题10分 ,第24题12分,共66分)
,第24题12分,共66分)

17.
(1)计算;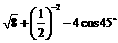 ;
;
(2)化简: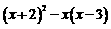 .
.
18.解方程: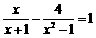 .
.
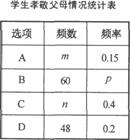
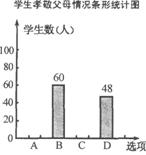
19.某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如右图表(部分信息未给出):
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中 ,
,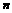 ,
,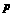 的值,并补全条形统计图.
的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
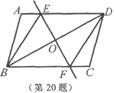
20.已知:如图,在 ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当么DOE等于多少度时,四边形BFDE为菱形?请说明理由.
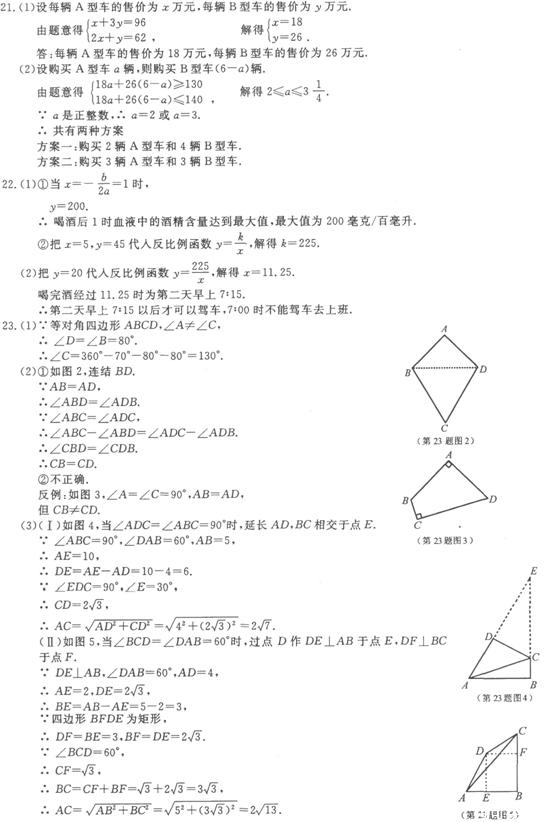
21.某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
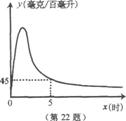
22.实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间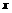 (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数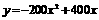 刻画;1.5时后(包括1.5时)y与
刻画;1.5时后(包括1.5时)y与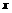 可近似地用反比例函数
可近似地用反比例函数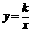 (
(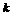 >O)刻画(如图所示).
>O)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当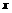 =5时,y=45.求
=5时,y=45.求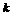 的值.
的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾 驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
23.类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
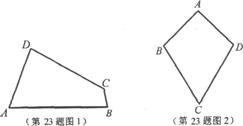
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度数.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜 想:“对于任意‘等对角四
想:“对于任意‘等对角四 边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形"ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.
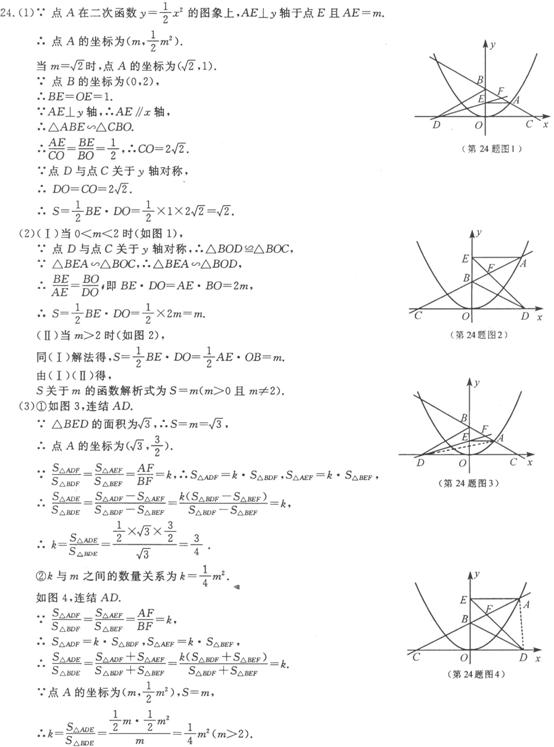
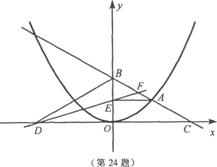
24.如图,在平面直角坐标系中,A是抛物 线
线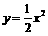 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交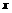 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为 ,△BED的面积为S.
,△BED的面积为S.
(1)当 =
=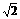 时,求S的值.
时,求S的值.
(2)求S关于 (
( ≠2)的函数解析式.
≠2)的函数解析式.
(3)①若S=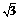 时,求
时,求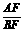 的值;
的值;
②当 >2时,设
>2时,设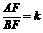 ,猜想
,猜想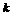 与
与 的数量关系
的数量关系 并证明.
并证明.
试题答案