(单词翻译:单击)
一、选择题（每小题3分，共15分）
1、下列各数中，最大的是（ B ）
A、0 B、2 C、－2 D、－1/2
2、下列事件中是必然事件是（ C ）
A、明天太阳从西边升起 B、篮球队员在罚球线投篮一次，未投中
C、实心铁球投入水中会沉入水底 D、抛出一枚硬币，落地后正面向上
3、下列电视台的台标中，是中心对称图形的是（ A ）
A、 B、 C、 D、
4、若x>y，则下列式子中错误的是（ D ）
A、x－3>y－3 B、 > C、x+3>y+3 D、－3x>－3y
5、如图1，把一块含有45°角的直角三角板两个顶点放在直尺的对边上，如果∠1=20°，则∠2的度数是（ C ）
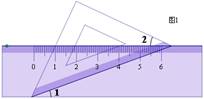
A、15° B、20° C、25° D、30°
二、填空题
6、4的平方根是 ±2 。
7、已知a+b=4，a－b=3，则a2－b2= 12 。
8、内角和与外角和相等的多边形的边数是 4 。
9、梅龙调整是广东梅州至福建龙岩高速公路，总投资59.57亿元。那么数据5 957 000 000用科学记数法表示是 5.957×109 。
10、写出一个三视图中主视图与俯视图完全相同的几何体的名称 正方体 。
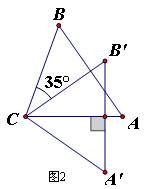
11、如图2，把⊿ABC绕点C按顺时针方向旋转35°，得到⊿A’B’C，A’B’交AC于点D，若∠A’DC=90°，则∠A= 55° 。
12、已知直线y=kx+b，若k+b=－5，kb=6，那么该直线不经过第 一 象限。
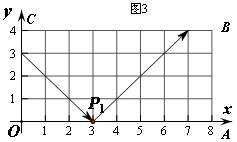
13、如图3，弹性小球从点P(0，3)出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角。当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，……第n次碰到矩形的边时的点为Pn。则点P2的坐标是 (8，3) ，点P2014的坐标是 (3，0) 。
三、解答题（有10小题，共81分）
14、本题满分7分。计算：(π－1)0+－()－1+ 。
解：原式＝1+2+－3+2
＝
15、本题满分7分。已知反比例函数y= 的图象经过点M(2，1)。
（1）求该函数的表达式；
（2）当2<x<4时，求y的取值范围。（直接写出结果）。
解：（1）把点M代入得k=2×1=2
∴y=
（2）<y<1
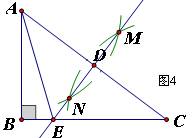
16、本题满分7分。如图，在Rt⊿ABC中，∠B=90°，分别以A、C为圆心，大于AC长为半径画弧，两弧相交于点M、N，作直线MN，与AC交于点D，与BC交于点E，连接AE。
（1）∠ADE= 90 °；
（2）AE = CE（填“>、<、=”）
（3）AB=3、AC=5时，⊿ABE的周长是 4 。
17、本题满分7分。某县为了解七年级学生对篮球、羽毛球、乒乓球、足球（以下分别用A、B、C、D表示）这四种球类运动的喜爱情况（每人只能选一种），对全县七年级学生进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）。
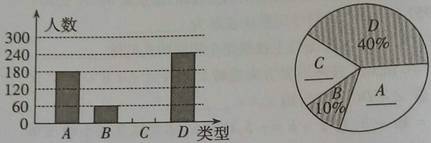
请根据以上信息回答：
（1）本次参加抽样调查的学生有 600 人；
（2）若全县七年级学生有4000人，估计喜爱足球（D）运动的人数是 240 人；
（3）在全县七年级学生中随机抽查一位，那么该学生喜爱乒乓球（C）运动的概率是 20% 。
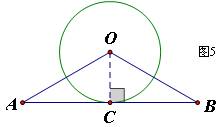（1）求证：AB与⊙O相切；
（2）若∠AOB=120°，AB=4，求⊙O的面积。
（1）证明：连接OC，
（2）∵C是边AB的中点，AB=4
∴BC=2
∵OA=OB，C是边AB的中点
∴中线OC可以表示高和∠AOB的平分线
∴在Rt⊿BOC中，∠BOC=60°，即有OC==2
S⊙O=4π
19、本题满分8分。已知关于x的方程x2+ax+a－2=0。
（1）当该方程的一个根为1时，求a的值及该方程的另一根；
（2）求证：不论a取何实数，该方程都有两个不相等的实数根。
（1）解：设方程的另一根为x1；
解得：a=，x1＝－
（2）证明：⊿＝a2－4×(a－2)= (a－2)2+4
∵(a－2)2≥0
∴⊿>0
∴不论a取何实数，该方程都有两个不相等的实数根。
20、本题满分8分。某校为美化校园，计划对面积为1800m2的区域进行绿化，安排甲、乙两个工程队完成。已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m2区域的绿化时，甲队比乙队少用4天。
（1）求甲、乙两工程队每天能完成绿化的面积分别是多少m2？
（2）若学校每天需付给甲队的绿化费用是0.4万元，乙队为0.25万元，要使这次的绿化总费不超过8万元，至少应安排甲队工作多少天？
解：（1）设乙队每天绿化x m2，则：
解得：x=50，2x=100
答：甲、乙两工程队每天能完成绿化的面积分别是100、50m2。
（2）设至少应安排甲队工作y天，则：
0.4y+×0.25≤8 y≥10
21、本题满分8分。如图6，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE。
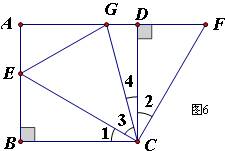
（1）求证：CE=CF；
（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？
（1）证明：
⇒⊿BCE≌⊿DCF⇒ CE=CF
（2）解：GE=BE+GD成立，理由是：7
⇒GE=BE+GD
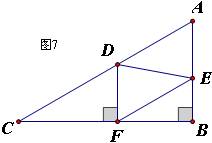
（1）求y与x的函数关系式；
（2）当四边形AEFD为菱形时，求x的值；
（3）当是⊿FED直角三角形时，求x的值。
解：（1）∵∠B=90°，AC=60，AB=30
∴∠C=30°
∴y=sin30°CD=
（2）当四边形AEFD为菱形时，有AD=DF
∴AC－CD=DF，即60－x=
∴x=40
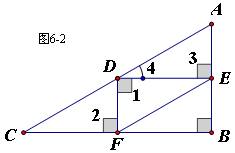
（3）当是⊿FED直角三角形时，只能是∠FDE=90°，如图6-2
由DF⊥BC得∠2=90°，即有DE//BC，所以四边形AEFD为平行四边形，显然AE=DF；
再由DE//BC可得：∠3=∠B=90°，∠4=∠C=30°
在Rt⊿BOC中，sin∠4==
∴AC－CD=2DF，即60－x= x
∴x=30
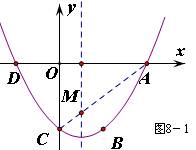
23、本题满分11分。如图8，已知抛物线y= x2－ x－3与x轴的交点为A、D（A在D的右侧），与y轴的交点为C。
（1）直接写出A、D、C三点的坐标；
（2）在抛物线的对称轴上找一点M，使得MD+MC的值最小，并求出点M的坐标；
（3）设点C关于抛物线对称的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，求出点P的坐标；若不存在，请说明理由。
解：（1）A(4，0) 、D(－2，0)、C(0，－3)
（2）连接AC，与抛物线的对称轴交点M即为所求，直线AC的解析式y=－3，
对称轴是直线x==1，把x=1代入y=－3得y=－
`∴M(1，－)
（3）如下图，当点P与D重合时，四边形ADCB是梯形，此时点P为(－2，0)；
直线AB的解析式为y=，过点C作CP1//AB，与抛物线交于点P1，
直线CP1的解析式为y=，联立y= x2－ x－3，可得P1(6，6)
