(单词翻译:单击)
一、选择题(共8小题,每小题3分,共24分)
1.3的相反数是( )
A. 3 B.-3 C.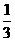 D.
D.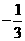

2.如图的几何体是由六个完全相同的正方体组成的,这个几何体的主视图是( )
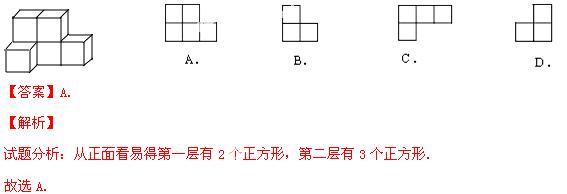
【考点】简单组合体的三视图.
3.《2013年大连市海洋环境状况公报》显示,2013年大连市管辖海域总面积为29000平方公里,29000用科学记数法表示为( )
A. 2.9×103 B.2.9×104 C.29×103 D. 0.29×105

【考点】科学记数法—表示较大的数.
4.在平面直角坐标系中,将点(2,3)向上平移1个单位,所得到的点的坐标是( )
A. (1,3) B. (2,2) C. (2,4) D. (3,3)
(3,3)

【考点】坐标与图形变化-平移.
5.下列计算正确的是( )
A. a+a2=a3 B.(3a)2=6a2 C.a6÷a2=a3 D.a2•a3=a5

【考点】1.同底数幂的除法;2.合并同类项;3.同底数幂的乘法;4.幂的乘方与积的乘方.
6.不等式组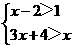 的解集是( )
的解集是( )
A. x>-2 B.x<-2 C.x>3 D. x<3

【考点】解一元一次不等式组.
7.甲口袋中有1个红球和1个黄球,乙口袋中有1个红球、1个黄球和1个绿球,这些球除颜色外都相同.从两个口袋中各随机取一个球,取出的两个球都是红的概率为( )
A.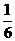 B.
B.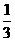 C.
C.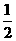 D.
D.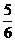
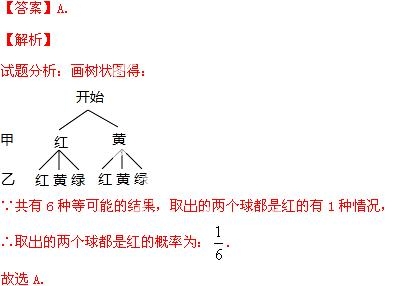
【考点】列表法与树状图法.
8.一个圆锥的高为4cm,底面圆的半径为3cm,则这个圆锥的侧面积为( )
A. 12πcm2 B.15πcm2 C.20πcm2 D.30πcm2

【考点】圆锥的计算.
二、填空题(共8小题,每小题3分,共24分)
9.分解因式:x2-4=

10.函数y= (x-1)2+3的最小值为
(x-1)2+3的最小值为
【答案】3.
【解析】

【考点】1.因式分解-运用公式法;2.代数式求值.
12.如图,△ABC中,D、E分别是AB、AC的中点,若BC=4cm,则DE= cm.
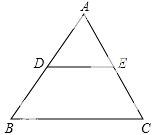

【考点】三角形中位线定理.
13.如图,菱形ABCD中,AC、BD相交于点O,若∠BCO=55°,则∠ADO= .
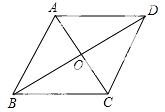
【答案】35°.
【解析】

【考点】菱形的性质.
14.如图,从一般船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得 灯塔顶部B的仰角为35°,则观
灯塔顶部B的仰角为35°,则观 测点A到灯塔BC的距离约为 m(精确到1m).
测点A到灯塔BC的距离约为 m(精确到1m).
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)
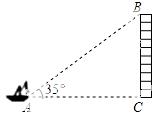
【答案 】59.
】59.
【解析】
试题分析:根据灯塔顶部B的仰角为35°,BC=41m,可得tan∠BAC=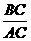 ,代入数据即可求出观测点A到灯塔BC的距离AC的长
,代入数据即可求出观测点A到灯塔BC的距离AC的长 度.
度.
试题解析:在Rt△ABC中,
∵∠BAC=35°,BC=41m,
∴tan∠ BAC=
BAC=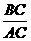 ,
,
∴AC=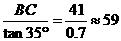 (m).
(m).
【考点】解直角三角形的应用-仰角俯角问题.
15.如表是某校女子排球队队员的年龄分布:
年龄 | 1 | 14 | 15 | 16 |
频数 | 1 | 2 | 5 | 4 |
则该 校女子排球队队员的平均年龄为 岁.
校女子排球队队员的平均年龄为 岁.

【考点】加权平均数.
16.点A(x1,y1)、B(x2,y2)分别 在双曲线y=
在双曲线y=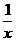 的两支上,若y1+y2>0,则x1+x2的范围是 .
的两支上,若y1+y2>0,则x1+x2的范围是 .

∵y1+y2>0,y1y2<0,
∴-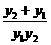 >0,即x1+x2>0.
>0,即x1+x2>0.
【考点】反比例函数图象上点的坐标特征.
三、解答题(本题共4小题,17.18.19各9分,20题12分,共39分)
17.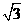 (1-
(1-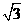 )+
)+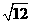 +(
+(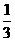 )-1.
)-1.

18.解方程: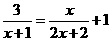 .
.

【考点】解分式方程.
19.如图:点A、B、C、D在一条直线上 ,AB=CD,AE∥BF,CE∥DF.求证:AE=BF.
,AB=CD,AE∥BF,CE∥DF.求证:AE=BF.
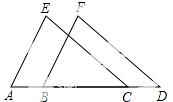
【答案】证明见解析.
【解析】
试题分析:根据两直线平行,同位角相等可得∠A=∠FBD,∠D=∠ACE,再求出AC=BD,然后利用“角边角”证明△ACE和△BDF全等,根据全等三角形对应边相等证明即可.

【考点】全等三角形的判定与性质.
20.某地为了解气温变化情况,对某月中午12时的气温(单位:℃)进行了统计.如表是根据有关数据制作的统计图表的一部分.
分组 | 气温x | 天数 |
A | 4≤x<8 | a |
B | 8≤x<12 | 6 |
C | 12≤x<16 | 9 |
D | 16≤x<20 | 8 |
E | 20≤x<24 | 4 |
根据以上信息解答下列问题:
(1)这个月中午1 2
2 时的气温在8℃至12℃(不含1
时的气温在8℃至12℃(不含1 2℃)的天数为 天,占这个月总天数的百分比为
2℃)的天数为 天,占这个月总天数的百分比为
%,这个月共有 天;
(2)统计表中的a= ,这个月中行12时的气温在 范围内的天数最多;
(3)求这个月中午12时的气温不低于16℃的天数占该月总天数的百分比.
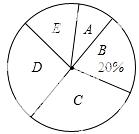
【答案】(1)6,20,30;(2)3,12≤x<16;(3)40%.
【解析】

【考点】1.频数(率)分布表;2.扇形统计图.
四、解答题(共3小题,其中21.22各9分,23题10分,共28分)
21.某工厂一种产品2013年的产量是100万件,计划2015年产量达到121万件.假设2013年到2015年这种产品产量的年增长率相同.
(1)求2013年到2015年这种产品产量的年增长率;
(2)2014年这种产品的产量应达到多少万件?

答:2013年到2015年这种产品产量的年增长率10%.
(2)2014年这种产品的产量为:100(1+0.1)=110(万件).
答:2014年这种产品的产量应达到110万件.
【考点】一元二次方程的应用.
22.小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即按原路匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.
(1)图中a= ,b= ;
(2)求小明的爸爸下山所用的时间.
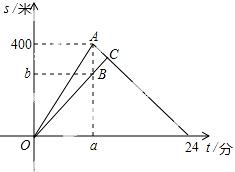
【答案】(1) a=8,b=280;(2) 14分.
【解析】

【考点】一次函数的应用.
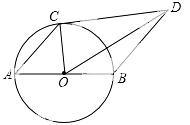
23.如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,BD∥AC.
(1)图中∠OCD= °,理由是 ;
(2)⊙O的半径为3,AC=4,求CD的长.
【答案】(1)90;圆的切线垂直于经过切点的半径;(3)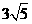 .
.
【解析】
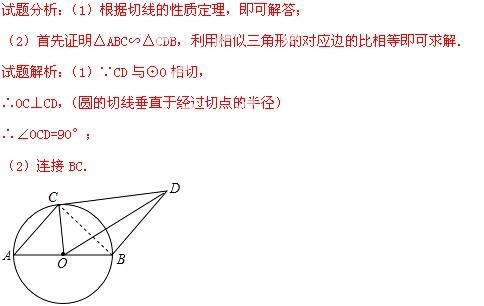
∵BD∥AC,
∴∠CBD=∠OCD=90°,
∴在直角△ABC中,BC=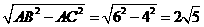 ,
,
∠A+∠ABC=90°,
∵OC=OB,
∴∠BCO=∠ABC,
∴∠A+∠BCO=90°,
又∵∠OCD=90°,即∠ BCO+∠BCD=90°,
BCO+∠BCD=90°,
∴∠BCD=∠A,
又∵∠CBD=∠OCD,
∴△ABC∽△CDB,
∴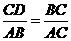 ,
,
∴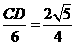 ,
,
解得:CD =
=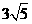 .
.
【考点】切线的性质.
五、解答题(共3题,其中24题11分,25.26各12分,共35分)
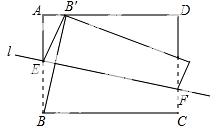
24.如图,矩形纸片ABCD中,AB=6,BC=8.折叠纸片使点B落在AD上,落点为B′.点B′从点A开始沿AD移动,折痕所在直线l的位置也随之改变,当直线l经过点A时,点B′停止移动,连接BB′.设直线l与AB相交于点E,与CD所在直线相交于点F,点B′的移动距离为x,点F与点C的距离为y.
(1)求证:∠BEF=∠AB′B;
(2)求y与x的函数关系式,并直接写出x的取值范围.
【答案】(1)证明见解析;(2)y=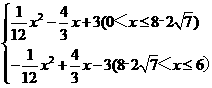 .
.
【解析】

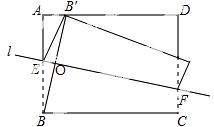
∴在等腰△BEB′中,EF是角平分线,
∴EF⊥BB′,∠BOE=90°,
∴∠ ABB′+∠BEF=90°,
ABB′+∠BEF=90°,
 ∵∠ABB′+∠AB′B=90°,
∵∠ABB′+∠AB′B=90°,
∴∠BEF=∠AB′B;
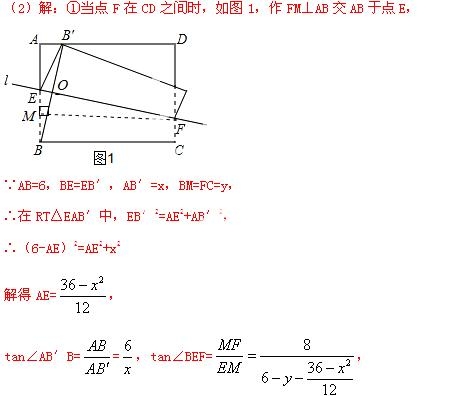
∵由(1)知∠B EF=∠AB′B,
EF=∠AB′B,
∴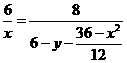 ,
,
化简,得y=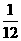 x2-x+3,(0<x≤8-2
x2-x+3,(0<x≤8-2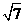 )
)
②当点F在点C下方时,如图2所示.
设直线EF与BC交于点K
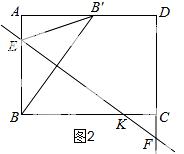
设∠ABB′=∠BKE=∠CKF=θ,则tanθ=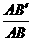 =
=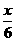 .
.
BK=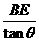 ,CK=BC-BK=8-
,CK=BC-BK=8-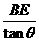 .
.
∴CF=CK•tanθ=(8-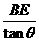 )•tanθ=8tanθ-BE=x-BE.
)•tanθ=8tanθ-BE=x-BE.

【考点】1.翻折变换(折叠问题);2.矩形的性质.
25.如图1,△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=DC,点F是DE与AC的交点,且DF =FE.
=FE.
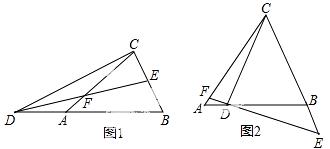
(1)图1中是否存在与∠BDE相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
(2)求证:BE=EC;
(3)若将“点D在BA的延长线上,点E在BC上”和“点F是DE与AC的交点,且DF=FE”分别改为“点D在AB上,点E在CB的延长线上”和“点F是ED的延长线与AC的交点,且DF=kFE”,其他条件不变(如图2).当AB=1,∠ABC=a时,求BE的长(用含k 、a的式子表示).
、a的式子表示).
【答案】(1)存在,证明见解析;(2)证明见解析;(3)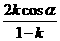 .
.
【解析】

∴∠BDE=∠DEC-∠DBC=∠DCE-∠ACB=∠DCA.
(2)过点E作EG∥AC,交AB于点G,如图1,
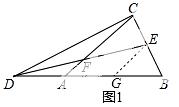
则有∠DAC=∠DGE.
在△DCA和△EDG中,
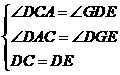
∴△DCA≌△EDG(AAS).
∴DA=EG,CA=DG.
 ∴DG=AB.
∴DG=AB.
∴DA=BG.
∵AF∥EG,DF=EF,
∴DA=AG.
∴AG=BG.
∵EG∥AC,
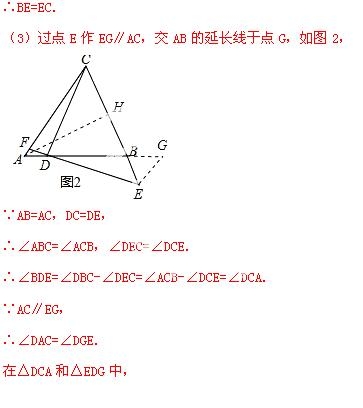
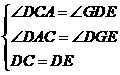
∴△DCA≌△EDG(AAS).
∴DA=EG,CA=DG
∴DG=AB=1.
∵AF∥EG,
∴△ADF∽△G DE.
DE.
∴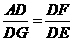 .
.
∵DF=kFE,
∴DE= EF-DF=(1-k)EF.
EF-DF=(1-k)EF.
∴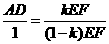 .
.
∴AD=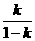 .
.
∴GE=AD=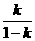 .
.
过点A作AH⊥BC,垂足为H,如图2,
∵AB=AC,AH⊥BC,
∴BH=CH.
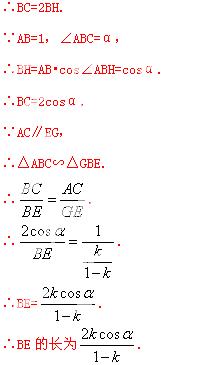
【考点】相似形综合题.
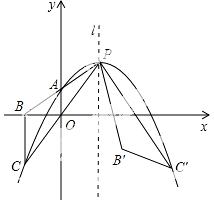
26.如图,抛物线y=a(x-m)2+2m-2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m- 1).连接并延长PA、P
1).连接并延长PA、P O,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.
O,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.
(1)该抛物线的解析式为 (用含m的式子表示);
(2)求证:BC∥y轴;
(3)若点B′恰好落在线段BC′上,求此时m的值.
【答案】(1) y=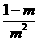 (x-m)2+2m-2.(2)证明见解析;(3)2+
(x-m)2+2m-2.(2)证明见解析;(3)2+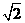 .
.
【解析】
试题分析:(1)只需将A点坐标(0,m-1)代入y=a(x-m)2+2m-2,即可求 出a值,从而得到抛物线的解析式.
出a值,从而得到抛物线的解析式.

(2)证明:如图1,
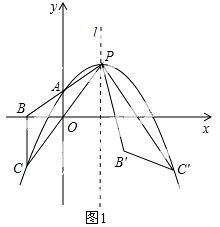
设直线PA的解析式为y=kx+b,
∵点P(m,2m-2),点A(0,m-1) .
.
∴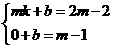 .
.

∴直线OP的解析式是y=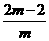 x.
x.
联立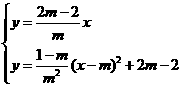
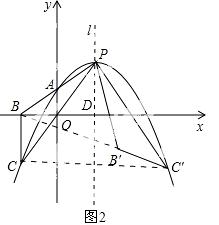
解得: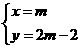 或
或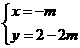 .
.
∵点C在第三象限,且m>1,
∴点C的横坐标是-m.
∴BC∥y轴.
(3)解:若点B′恰好落在线段BC′上,
设对称轴l与x轴的交点为D,连接CC′,如图2,
则有∠PB'C'+∠PB'B=180°.
∵△PB′C′是由△PBC绕点P逆时针旋转所得,
∴∠PBC=∠PB'C',PB=PB′,∠BPB′=∠CPC′.
∴∠PBC+∠PB'B=180°.
∵BC∥AO,
∴∠ABC+∠BAO=180°.
∴∠PB'B=∠BAO.
∵PB=PB′,PC=PC′,
∴∠PB′B=∠PBB′=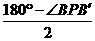 ,
,
∴∠PCC′=∠PC′C=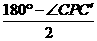 .
.




