(单词翻译:单击)
SAT数学虽然简单,也需要我们努力备考。下面天道小编为大家具体介绍SAT数学分析:Lines and Distance,希望对大家备考SAT数学考试有所帮助。
SAT(Scholastic Assessment Test)是美国高中生进入美国大学需要参加的考试,也就是美国的“高考”。近年来,越来越多的准备去美国读本科的中国高中生开始参加SAT的考试。
Lines and distance are fundamental to coordinate geometry, not to mention to the Math IC test. Even the most complicated coordinate geometry question uses the concepts covered in the next few sections.
DistanceMeasuring distance in the coordinate plane is made possible thanks to the Pythagorean theorem. If you are given two points, (x1,y1), and (x2,y2), their distance from each other is given by the following formula:
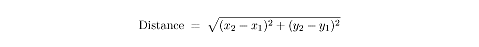
The diagram below shows how the Pythagorean theorem plays a role in the formula. The distance between two points can be represented by the hypotenuse of a right triangle whose legs are lengths (x2 – x1) and (y2 – y1).
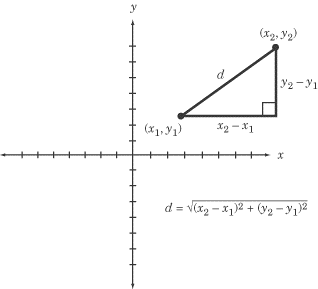
To calculate the distance from (4, –3) to (–3, 8), plug the coordinates into the formula:The distance between the points is , which equals approximately 13.04. You can double-check this answer by plugging it back into the Pythgorean theorem.Finding MidpointsThe midpoint between two points in the coordinate plane can be calculated using a formula. If the endpoints of a line segment are (x1, y1) and (x2, y2), then the midpoint of the line segment is:In other words, the x- and y-coordinates of the midpoint are the averages of the x- and y-coordinates of the endpoints.Here’s a practice question:What is the midpoint of the line segment whose endpoints are (6, 0) and (3, 7)?To solve, all you need to do is plug the points given into the midpoint formula . x1 = 6, y1 = 0, x2 = 3, and y2 = 7:
以上便是SAT数学分析:Lines and Distance的介绍,非常详细,希望对大家有所帮助,各位考生可以根据自己的具体情况有选择地进行借鉴,天道小编祝大家都能取得理想的SAT数学考试成绩!


