数学模拟题

　　1. The area of a rectangle with sides x and 3x, is how many times greater than the area of a right angled isosceles triangle with side x?

　　2. If $81 is to be divided among n people, where n > 1, so that each gets $x, where x is a whole number > 1, how many different values could there be for n?

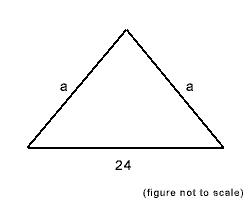
　　3. If the area of the triangle shown above is 108 square centimeters, what is its perimeter in centimeters?

　　4. A charity organisation sells greetings cards in packs costing $10 or $2.50 each. A total of 75 packs were sold at a fair for a total of $375. How many of the $2.50 packs were sold?

　　5. The length of a rectangle is 2/7 of the perimeter. What is the value of the diagonal of the rectangle if the perimeter is 14 units?

　　6. A = {A, B, C, D, E, F, G}

　　B = {0, 1, 2}

　　C = {1, 2, 3, 4, 5, 6, 7, 8, 9}

　　The filing system in an office requires each file to have an alphanumeric code name of the form abc. A, B and C are the sets from which a,b, and c must be chosen. How many possible code names are there?

　　7. A measuring cylinder is filled one third full with ethanol. A mixture of ethanol, water and propanol is used to fill the measuring flask to capacity. What fraction of the final mixture is ethanol?

　　8. The equation y = 6 is graphed on the same coordinate axes as the circle with center (4,4) and radius 3.

　　One of the points of intersection of the line and the circle has x-coordinate 1.76. What is the x coordinate of the other point of intersection?

　　9. If a and b are positive integers, and (ab3/2)2 = 108, what is the value of ab?

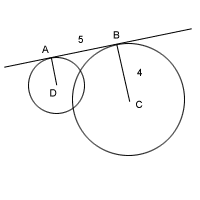
　　10. The line through AB is tangent to two circles with centers D and C and whose areas are in the ratio 4: 1

　　If AB = 5 and BC =4, what is the length of line segment DC (not shown)? Grid your answer correct to three significant figures.

参答案

　　参考答案:

　　1.Correct Answer: 6

　　Explanation:

　　The area of the rectangle is 3x²

　　Area of right isosceles triangle = ½ x²

　　Divide the area of the rectangle by the area of the triangle

　　3x²/ ½ x² = 6

　　2.Correct Answer: 3

　　Explanation:

　　n must be a factor if the result of dividing 81 by n is a whole number.

　　Factorize 81 to give factors of 9, 3, 27

　　Therefore n can take 3 different values

　　3.Correct Answer: 54

　　Explanation:

　　Draw out the figure and add a perpendicular height from the base.

　　Since area = ½ base x height, and area = 108

　　108 = 12 x height = 9

　　Now you need to recognize that each triangle formed by half the base, the height and the side marked �a�, is a 3-4-5 right triangle. Therefore �a� = 15

　　Perimeter of the large triangle = 24 + 15 + 15 = 54

　　4.Correct Answer: 50

　　Explanation:

　　Frame an equation. Let the number of $2.50 packs be n. the number of 410 packs sold = 75 - n.

　　Total cost = n (2.5) + (75-n)10

　　375 = 2.5n + 750 - 10n

　　7.5n = 375; n = 50

　　5.Correct Answer: 5

　　Explanation:

　　Half the perimeter = length + breadth = 7

　　The length = 2/7 x 14 = 4; the breadth = 7 - 4 = 3

　　The length and the breadth form the legs of a 3-4-5 right triangle with the diagonal of the rectangle forming the hypotenuse. So the diagonal = 5

　　6.Correct Answer: 189

　　Explanation:

　　We have a choice of 1/7 for a, 1/3 for b and 1/9 for c. Therefore we have 7 x 3 x 9 = 189 possible code names. (You multiply the choices because any one from a set can be combined with any from the other sets)

　　7.Correct Answer: 5/9

　　Explanation:

　　If one third is full, then 2/3 is empty initially. One third of the mixture that is to be added is ethanol. Therefore we are adding 1/3 x 2/3 ethanol = 2/9

　　But the flask already has 1/3 ethanol. New fraction will be 1/3 + 2/9 = 5/9

　　8.Correct Answer: 6.24

　　Explanation:

　　Draw a sketch. The points of intersection will lie symmetrically: one will be x units to the right of the center of the circle and one will be x units to the left. The x-coordinate of the center of the circle is 4, and so 1.76 lies (4 � 1.76) = 2.24 units to the left and the other point will lie 2.24 units to the right = 4 + 2.24 = 6.24

　　9.Correct Answer: 6

　　Explanation:

　　First simplify by taking out the brackets: a²b6/2 =108 ; a²b³ = 108

　　Now we are stuck unless we realize that if a and b are both integers there is probably only one solution to this equation, which we should be able to find if we find the prime factors of 108.

　　108 = 2 x 2 x 3 x 3 x 3 x 3, and so a must be 2 and b must be 3. Hence, ab = 6

　　10.Correct Answer: 5.39

　　Explanation:

　　Angles DAB and ABC are right angles. Because the areas of the circles are in the ratio of 4:1 the radii must be in the ratio of √4:√1 which is 2: 1. We are told the radius (BC) of the larger circle is 4, hence, the radius of the smaller circle must be 2.

　　If we draw a line from D perpendicular to BC we divide ABCD into a rectangle and a right triangle. The right triangle has sides 5 (because it is equal to AB), 2 (half of BC), and DC. Using Pythagoras theorem we have 5² + 2² = DC² DC = √29 = 5.3852 To three significant figures this is 5.39 (We can�t grid in more anyway)