数学模拟题

　　Question 1: How many integers between 1 and 50 contain the digit 3?

　　Question 2: |2·x + 1| = 3 |x + 5| = 6

　　What value of x satisfies both of the equations above?

　　Question 3: The length of rectangle B is 50% longer than the length of rectangle A and the width of rectangle B is 50% shorter than the width of rectangle A. What is the ratio between the area of rectangle B and the area of rectangle A?

　　Question 4: If a§b = ab + ba for all real numbers a,b, what is (2§3)§1?

　　Question 5: What is the value of the x + y sum, if x + 2y = 5 and 2x + y = 7 ?

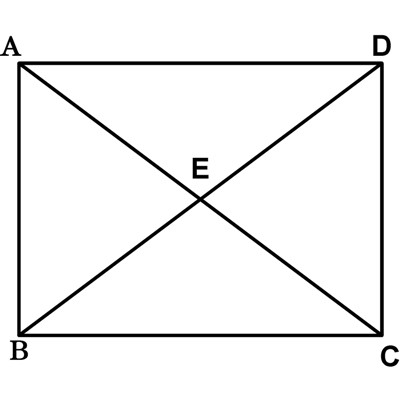
　　Question 6: If AC and BD are the diagonals of the ABCD rectangle and EAB is equilateral, what is the value of angle ADE?

　　Question 7: The average of a set of 11 numbers is 11. If two numbers are removed the average of the remaining numbers is 10. What is the sum of the two numbers removed?

　　Question 8: Last year, the price of a computer monitor was $300.What is the percent increase in price, if it is available now at $360?

　　Question 9: In the x, y plane, what is the area of the triangle created by the x axis, the y axis and the y = (-5/4)x + 5 line?

　　Question 10: If a coin is flipped twice, what is the probability that it will land heads at least once?

参答案

　　参考答案:

　　参考答案与解析

　　Question 1: How many integers between 1 and 50 contain the digit 3?

　　Answer: 14

　　Explanation: There are 14 integers between 1 and 50 that contain

　　the digit 3: 3, 13, 23, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 43.

　　Question 2: |2x + 1| = 3 |x + 5| = 6

　　What value of x satisfies both of the equations above?

　　Answer: 1

　　Explanation: Since |2x + 1| = 3, the value of 2x + 1 is either 3 or -3.

　　2x + 1 = 3

　　2x = 2

　　x = 1

　　2x + 1 = -3

　　2x = -4

　　x = -2

　　The two values of x that satisfy the first equation are 1 and -2.

　　Since |x + 5| = 6, the value of x + 5 is either 6 or -6.

　　x + 5 = 6

　　x = 1

　　x + 1 = -6

　　x = -7

　　The two values of x that satisfy the second equation are 1 and -6.

　　You are asked to find the value of x that satisfies both equations and that value is 1.

　　Question 3: The length of rectangle B is 50% longer than the length of rectangle A and

　　the width of rectangle B is 50% shorter than the width of rectangle A. What is the ratio

　　between the area of rectangle B and the area of rectangle A?

　　Answer: .75

　　Explanation: The area of rectangle A is AreaA = lA·wA

　　The area of rectangle B is AreaB = lB·wB = 1.5·lA·.5·wA = .75·lA·wA

　　The ratio between the area of rectangle B and the area of rectangle A is:

　　AreaB/AreaA = (.75·lA·wA)/(lA·wA) = .75

　　Question 4: If a§b = ab + ba for all real numbers a,b, what is (2§3)§1?

　　Answer: 18

　　Explanation: 2§3 = 23 + 32 = 8 + 9 = 17

　　17§1 = 171 + 117 = 17 + 1 = 18

　　In conclusion, (2§3)§1 = 18

　　Question 5: What is the value of the x + y sum, if x + 2y = 5 and 2x + y = 7 ?

　　Answer: 4

　　Explanation: The easiest way to find x + y is to realize that by adding

　　the 2 equations, the left term of the addition is a multiple of x + y:

　　3(x + y) = 12

　　x + y = 4

　　You can also solve the system of 2 equations, find x and y and add them,

　　but this will likely take longer.

　　Question 6: If AC and BD are the diagonals of the ABCD rectangle and EAB is equilateral,

　　what is the value of angle ADE?

　　Answer: 30o

　　Explanation: Rectangles have parallel opposite sides so AD and BC are parallel.

　　The BD diagonal produces congruent angles: angle ADE is equal to angle CBD.

　　ABCD is a rectangle so angle ABC is 90o.

　　ABE is equilateral so angle ABE is 60o.

　　Angle ADE = Angle CBD = Angle ABC - Angle ABD = 90o - 60o = 30o

　　Question 7: The average of a set of 11 numbers is 11. If two numbers are removed

　　the average of the remaining numbers is 10. What is the sum of the two numbers removed?

　　Answer: 31

　　Explanation: The average of the 11 numbers is equal with the sum of the numbers divided by 11.

　　11 = (sum of 11 numbers)/11

　　Sum of 11 numbers = 11·11

　　Sum of 11 numbers = 121

　　If x and y are the 2 numbers removed,

　　[(Sum of 11 numbers) - x - y]/9 = 10

　　[121 - x - y] = 10·9

　　[121 - x - y] = 90

　　x + y = 121 - 90

　　x + y = 31

　　Question 8: Last year, the price of a computer monitor was $300.What is the percent increase in price,

　　if it is available now at $360?

　　Answer: 20%

　　Explanation: The percent increase in price is the actual change in price,

　　divided by the original price, and multiplied by 100.

　　($360 - $300)·100/$300 = 20%

　　Question 9: In the x, y plane, what is the area of the triangle created by the x axis, the y axis and the y = (-5/4)x + 5 line?

　　Answer: 10

　　Explanation:

　　y = (-5/4)x + 5 intersects the y axis at x = 0 and y = 5

　　y = (-5/4)x + 5 intersects the x axis at y = 0 and x = 4

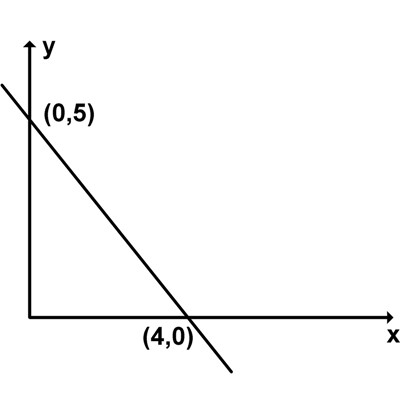
　　The triangle created by the x axis, the y axis and the y = (-5/4)x + 5 line is a right triangle.

　　The area of the triangle is A = (1/2)·4·5 = 10.

　　Question 10: If a coin is flipped twice, what is the probability that it will land heads at least once?

　　Answer: .75

　　Explanation:

　　The 4 possible combinations are (heads,heads), (heads,tails), (tails,heads) and (tails,tails).

　　Three of these four combinations satisfy the conditions that the coin lands heads at least once.

　　The probability is 3/4 = .75