(单词翻译:单击)
第Ⅰ卷
一、选择题
(1)设集合U=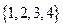 ,
,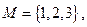
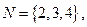 则
则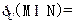
(A)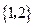 (B)
(B)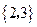 (C)
(C)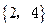 (D)
(D)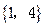
【答案】D
【命题意图】本题主要考查集合交并补运算.
【解析】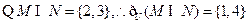
(2)函数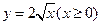 的反函数为
的反函数为
(A)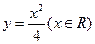 (B)
(B)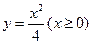
(C)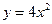
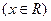 (D)
(D)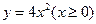
【答案】B
【命题意图】本题主要考查反函数的求法.
【解析】由原函数反解得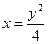 ,又原函数的值域为
,又原函数的值域为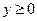 ,所以函数
,所以函数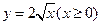 的反函数为
的反函数为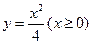 .
.
(3)设向量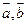 满足
满足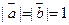 ,
,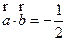 ,则
,则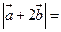
(A)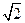 (B)
(B)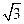 (C)
(C)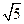 (D)
(D)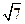
【答案】B
【命题意图】本题主要考查平面向量的数量积与长度的计算方法.
【解析】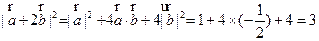 ,所以
,所以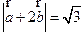
(4)若变量x,y满足约束条件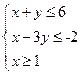 ,则
,则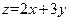 的最小值为
的最小值为
(A)17 (B)14 (C)5 (D)3
【答案】C
【命题意图】本题主要考查简单的线性规划.
【解析】作出不等式组表示的可行域,从图中不难观察当直线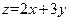 过直线x=1与x-3y=-2的交点(1,1)时取得最小值,所以最小值为5.
过直线x=1与x-3y=-2的交点(1,1)时取得最小值,所以最小值为5.
(5)下面四个条件中,使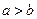 成立的充分而不必要的条件是
成立的充分而不必要的条件是
(A)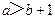 (B)
(B)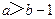 (C)
(C)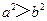 (D)
(D)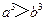
【答案】A
【命题意图】本题主要考查充要条件及不等式的性质.
【解析】即寻找命题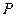 ,使
,使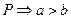 ,且
,且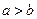 推不出
推不出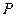 ,逐项验证知可选A.
,逐项验证知可选A.
(6)设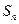 为等差数列
为等差数列
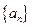 的前
的前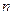 项和,若
项和,若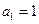 ,公差
,公差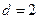 ,
,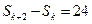 ,则
,则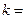
(A)8 (B)7 (C)6 (D)5
【答案】D
【命题意图】本题主要考查等差数列的基本公式的应用.
【解析】解法一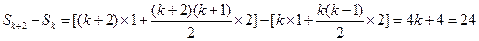 ,解得
,解得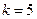 .
.
解法二: 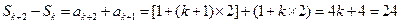 ,解得
,解得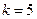 .
.
(7)设函数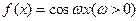 ,将
,将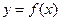 的图像向右平移
的图像向右平移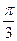 个单位长度后,所得的图像与原图像重合,则
个单位长度后,所得的图像与原图像重合,则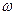 的最小值等于
的最小值等于
(A)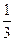 (B)
(B)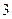 (C)
(C)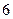 (D)
(D)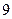
【答案】C
【命题意图】本题主要考查三角函数的周期性与三角函数图像变换的关系.
【解析】由题意将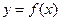 的图像向右平移
的图像向右平移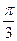 个单位长度后,所得的图像与原图像重合,说明了
个单位长度后,所得的图像与原图像重合,说明了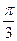 是此函数周期的整数倍,得
是此函数周期的整数倍,得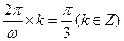 ,解得
,解得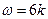 ,又
,又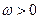 ,令
,令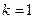 ,得
,得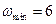 .
.
(8)已知直二面角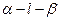 ,点
,点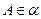 ,
,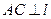 ,
,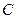 为垂足,
为垂足,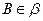 ,
,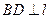 ,
,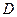 为垂
为垂
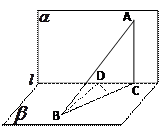 足,若
足,若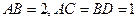 ,则
,则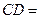
(A) 2 (B)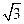 (C)
(C)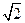 (D)1
(D)1
【答案】C
【命题意图】本题主要考查二面角的平面角及解三角形.
【解析】因为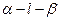 是直二面角,
是直二面角, 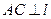 ,∴
,∴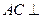 平面
平面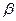 ,
,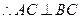
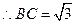 ,又
,又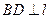 ,
,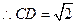
(9) 4位同学每人从甲、乙、丙3门课程中选修1门,则恰有2人选修课程甲的不同选法共有
(A) 12种 (B) 24种 (C) 30种 (D)36种
【答案】B
【命题意图】本题主要考查两个原理与排列组合知识,考察考生分析问题的能力.
【解析】第一步选出2人选修课程甲有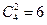 种方法,第二步安排剩余两人从乙、丙中各选1门课程有
种方法,第二步安排剩余两人从乙、丙中各选1门课程有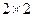 种选法,根据分步计数原理,有
种选法,根据分步计数原理,有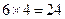 种选法.
种选法.
(10) 设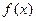 是周期为2的奇函数,当
是周期为2的奇函数,当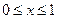 时,
时,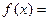
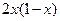 ,则
,则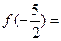
(A) -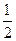 (B)
(B)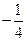 (C)
(C)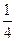 (D)
(D)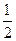
【答案】A
【命题意图】本题主要考查利用函数的周期性和奇偶性求函数值的方法. 关键是把通过周期性和奇偶性把自变量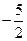 转化到区间[0,1]上进行求值.
转化到区间[0,1]上进行求值.
【解析】由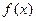 是周期为2的奇函数,利用周期性和奇偶性得:
是周期为2的奇函数,利用周期性和奇偶性得: 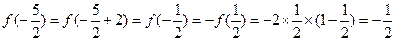
(11)设两圆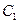 、
、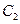 都和两坐标轴相切,且都过点(4,1),则两圆心的距离
都和两坐标轴相切,且都过点(4,1),则两圆心的距离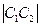 =
=
(A)4 (B)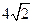 (C)8 (D)
(C)8 (D)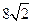
【答案】C
【命题意图】本题主要考查圆的方程与两点间的距离公式.
【解析】由题意知圆心在直线y=x上并且在第一象限,设圆心坐标为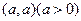 ,则
,则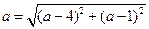 ,即
,即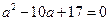 ,所以由两点间的距离公式可求出
,所以由两点间的距离公式可求出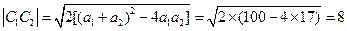 .
.
(12)已知平面α截一球面得圆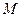 ,过圆心
,过圆心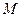 且与α成
且与α成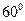 二面角的平面β截该球面得圆
二面角的平面β截该球面得圆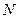 .若该球面的半径为4,圆
.若该球面的半径为4,圆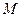 的面积为4
的面积为4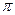 ,则圆
,则圆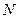 的面积为
的面积为
(A)7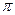 (B)9
(B)9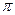 (C)11
(C)11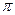 (D)13
(D)13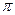
【答案】D
【命题意图】本题主要考查二面角的概念与球的性质.
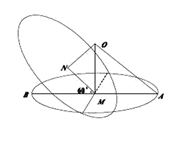
【解析】如图所示,由圆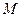 的面积为4
的面积为4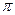 知球心
知球心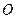 到圆
到圆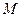 的距离
的距离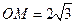 ,在
,在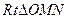 中,
中,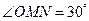 , ∴
, ∴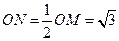 ,故圆
,故圆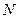 的半径
的半径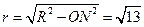 ,∴圆
,∴圆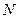 的面积为
的面积为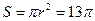 .
.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横 线上.
线上.
(注意 :在试卷上作答无效)
:在试卷上作答无效)
(13)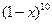 的二项展开式中,
的二项展开式中,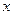 的系数与
的系数与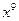 的系数之差为
的系数之差为  .
.
【答案】0
【命题意图】本题主要考查二项展开式的通项公式和组合数的性质.
【解析】由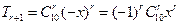 得
得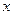 的系数为
的系数为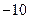 ,
,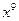 的系数为
的系数为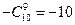 ,所以
,所以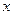 的系数与
的系数与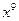 的系数之差为0.
的系数之差为0.
(14)已知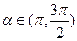 ,
,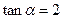 ,则
,则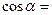
 .
.
【答案】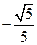
【命题意图】本题主要考查同角三角函数的基本关系式. 要注意角的范围,进而确定值的符号.
【解析】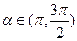 ,
,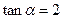 ,则
,则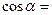
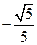 .
.
(15)已知正方体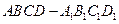 中,E为
中,E为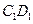 的中点,则异面直线AE与BC所成角的余弦值为 .
的中点,则异面直线AE与BC所成角的余弦值为 .
【答案】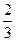
【命题意图】本题主要考查正方体中异面直线AE与BC所成的角.
【解析】取A1B1的中点M连接EM,AM,AE,则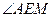 就是异面直线AE与BC所成的角。在
就是异面直线AE与BC所成的角。在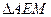 中,
中,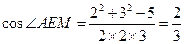 .
.
(16)已知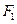 、
、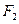 分别为双曲线
分别为双曲线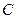 :
: 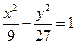 的左、右焦点,点
的左、右焦点,点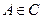 ,点
,点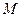 的坐标为(2,0),
的坐标为(2,0),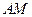 为
为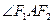 的平分线.则
的平分线.则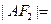 .
.
【答案】6
【命题意图】本题主要考查三角形的内角平分线定理,双曲线的第一定义和性质.
【解析】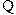
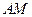 为
为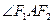 的平分线,∴
的平分线,∴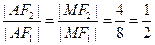 ∴
∴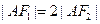
又点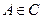 ,由双曲线的第一定义得
,由双曲线的第一定义得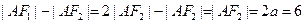 .
.
三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分l0分)(注意:在试题卷上作答无效)
设等比数列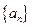 的前n项和为
的前n项和为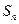 .已知
.已知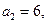
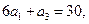 求
求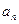 和
和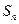 .
.
【思路点拨】解决本题的突破口是利用方程的思想建立关于a1和公比q的方程,求出a1和q,然后利用等比数列的通项公式及前n项和公式求解即可。
【解析】设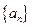 的公比为q,由题设得
的公比为q,由题设得
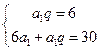 …………………………………3分
…………………………………3分
解得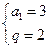 或
或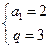 , …………………………………6分
, …………………………………6分
当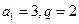 时,
时,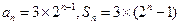 ;
;
当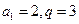 时,
时,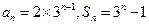 ……………………………10分
……………………………10分
(18)(本小题满分12分)(注意:在试题卷上作答无效)
△ABC的内角A、B、C的对边分别为a、b、c.己知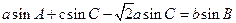 .
.
(Ⅰ)求B;
(Ⅱ)若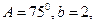
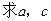 .
.
【思路点拨】第(I)问由正弦定理把正弦转化为边,然后再利用余弦定理即可解决。
(II)在(I)问的基础上知道两角一边可以直接利用正弦定理求解.
【解析】(I)由正弦定理得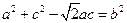 …………………………3分
…………………………3分
由余弦定理得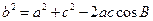 .
.
故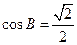 ,因此
,因此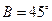 .…………………………………6分
.…………………………………6分
(II)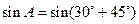
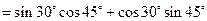
 …………………………………8分
…………………………………8分
故 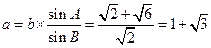
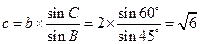 .…………………………………12分
.…………………………………12分
(19)(本小题满 分l2分)(注意:在试题卷上作答无效)
分l2分)(注意:在试题卷上作答无效)
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立.
(I)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(II)求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率.
【命题意图】本题主要考查独立事件的概率、对立事件的概率、互斥事件的概率及次独立重复试验发生k次的概率,考查考生分析问题、解决问题的能力.
【解析】记A表示事件:该地的1位车主购买甲种保险:
B表示事件:该地的1位车主购买乙种保险但不购买甲种保险。
C表示事件:该地的1位车主至少购买甲、乙两种保险中的1种;
D表示事件:该地的1位车主甲、乙两种保险都不购买;
E表示事件:该地的3位车主中恰有1位车主甲、乙两种保险都不购买.
(I)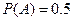 ,
, 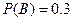 ,
, 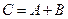 ……………………………3分
……………………………3分
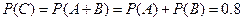 ……………………………6分
……………………………6分
(II)D=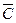 ,P(D)=1-P(C)=1-0.8=0.2, ……………………………9分
,P(D)=1-P(C)=1-0.8=0.2, ……………………………9分
P(E)=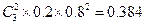 . ……………………………12分
. ……………………………12分
(20)(本小题满 分l2分)(注意:在试题卷上作答无效)
分l2分)(注意:在试题卷上作答无效)
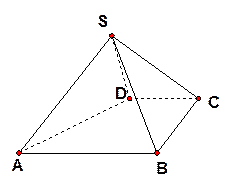
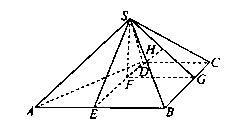
如图,四棱锥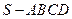 中,
中, 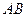 ∥
∥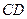 ,
,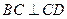 ,侧面
,侧面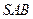 为等边三角形.
为等边三角形.
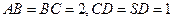 .
.
(I) 证明: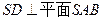
(II) 求AB与平面SBC所成角的大小。
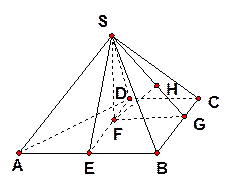
【分析】第(I)问的证明的突破口是利用等边三角形SAB这个条件,找出AB的中点E,连结SE,DE,就做出了解决这个问题的关键辅助线。
(II)本题直接找线面角不易找出,要找到与AB平行的其它线进行转移求解。
【命题意图】以四棱锥为载体考查线面垂直证明和线面角的计算,注重与平面几何的综合.
解法一:(Ⅰ)取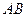 中点
中点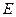 ,连结
,连结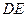 ,则四边形
,则四边形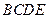 为矩形,
为矩形,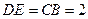 ,连结
,连结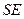 ,则
,则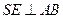 ,
,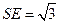 .
.
又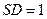 ,故
,故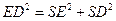 ,
,
所以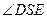 为直角. ………………3分
为直角. ………………3分
由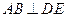 ,
,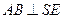 ,
,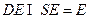 ,得
,得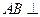 平面
平面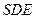 ,所以
,所以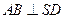 .
.
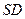 与两条相交直线
与两条相交直线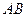 、
、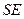 都垂直.
都垂直.
所以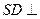 平面
平面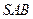 . ………………6分
. ………………6分
另解:由已知易求得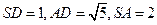 ,于是
,于是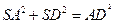 .可知
.可知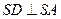 ,同理可得
,同理可得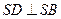 ,又
,又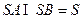 .所以
.所以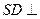 平面
平面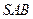 . ………………6分
. ………………6分
(Ⅱ)由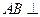 平面
平面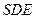 知,平面
知,平面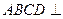 平面
平面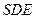 .
.
作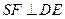 ,垂足为
,垂足为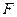 ,则
,则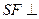 平面ABCD,
平面ABCD,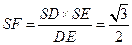 .
.
作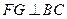 ,垂足为
,垂足为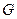 ,则
,则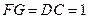 .
.
连结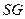 .则
.则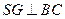 .
.
又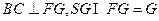 ,故
,故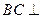 平面
平面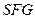 ,平面
,平面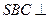 平面
平面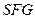 .……9分
.……9分
作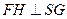 ,
,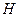 为垂足,则
为垂足,则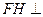 平面
平面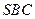 .
.
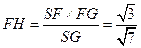 ,即
,即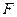 到平面
到平面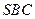 的距离为
的距离为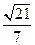 .
.
由于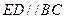 ,所以
,所以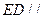 平面
平面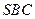 ,
,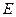 到平面
到平面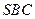 的距离
的距离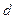 也为
也为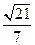 .
.
设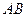 与平面
与平面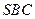 所成的角为
所成的角为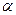 ,则
,则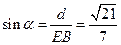 ,
,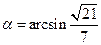 .……12分
.……12分
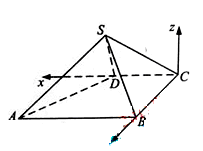
解法二:以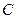 为原点,射线
为原点,射线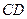 为
为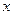 轴的正半轴,建立如图所示的空间直角坐标系
轴的正半轴,建立如图所示的空间直角坐标系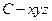 .
.
设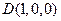 ,则
,则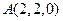 、
、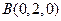 .
.
又设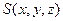 ,则
,则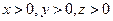 .
.
(Ⅰ)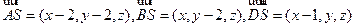 ,
,
由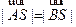 得
得
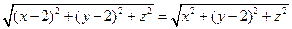 ,
,
故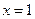 .
.
由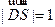 得
得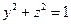 ,
,
又由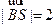 得
得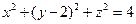 ,
,
即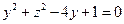 ,故
,故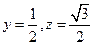 . ………………3分
. ………………3分
于是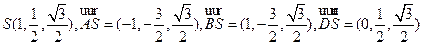 ,
,
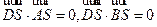 .
.
故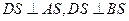 ,又
,又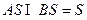 ,
,
所以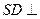 平面
平面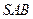 . ………………6分
. ………………6分
(Ⅱ)设平面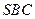 的法向量
的法向量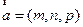 ,
,
则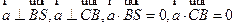 .
.
又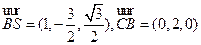 ,
,
故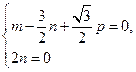 ………………9分
………………9分
取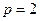 得
得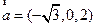 ,又
,又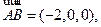
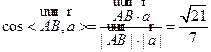 .
.
故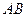 与平面
与平面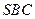 所成的角为
所成的角为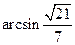 . ………………12分
. ………………12分
(21)(本小题满分l2分)(注意:在试题卷上作答无效)
已知函数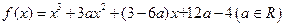

(Ⅰ)证明:曲线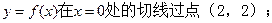
(Ⅱ)若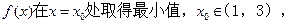 求a的取值范围.
求a的取值范围.
【分析】第(I)问直接利用导数的几何意义,求出切线的斜率,然后易写出切线方程.
(II)第(II)问是含参问题,关键是抓住方程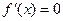 的判别式进行分类讨论.
的判别式进行分类讨论.
解:(I)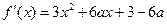 .………………2分
.………………2分
由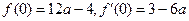 得曲线
得曲线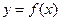 在x=0处的切线方程为
在x=0处的切线方程为
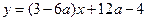
由此知曲线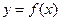 在x=0处的切线过点(2,2) .………………6分
在x=0处的切线过点(2,2) .………………6分
(II)由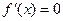 得
得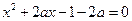 .
.
(i)当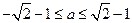 时,
时,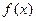 没有极小值; .………………8分
没有极小值; .………………8分
(ii)当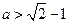 或
或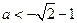 时,由
时,由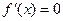 得
得
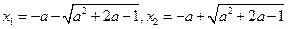
故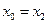 .由题设知
.由题设知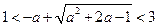 ,
,
当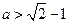 时,不等式
时,不等式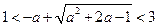 无解;
无解;
当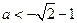 时,解不等式
时,解不等式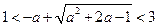 得
得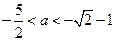
综合(i)(ii)得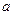 的取值范围是
的取值范围是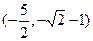 ..………………12分
..………………12分
(22)(本小题满分l2分)(注意:在试题卷上作答无效)
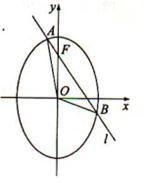
已知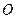 为坐标原点,
为坐标原点,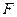 为椭圆
为椭圆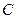 :
: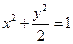 在
在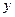 轴正半轴上的焦点,过
轴正半轴上的焦点,过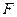 且斜率为
且斜率为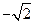 的直线
的直线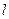 与
与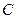 交与
交与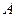 、
、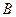 两点,点
两点,点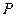 满
满 足
足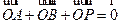 .
.
(I)证明:点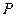 在
在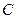 上;
上;
(II)设点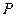 关于点
关于点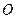 的对称点为
的对称点为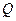 ,证明:
,证明: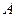 、
、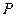 、
、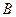 、
、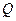 四点在同一圆上.
四点在同一圆上.
【命题意图】本题考查直线方程、平面向量的坐标运算、点与曲线的位置关系、曲线交点坐标求法及四点共圆的条件。
【分析】方程联立利用韦达定理是解决这类问题的基本思路,注意把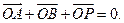 用坐标表示后求出P点的坐标,然后再结合直线方程把P点的纵坐标也用A、B两点的横坐标表示出来.从而求出点P的坐标代入椭圆方程验证即可证明点P在C上;(II)此问题证明有两种思路:思路一:关键是证明
用坐标表示后求出P点的坐标,然后再结合直线方程把P点的纵坐标也用A、B两点的横坐标表示出来.从而求出点P的坐标代入椭圆方程验证即可证明点P在C上;(II)此问题证明有两种思路:思路一:关键是证明 互补.通过证明这两个角的正切值互补即可,再求正切值时要注意利用到角公式.
互补.通过证明这两个角的正切值互补即可,再求正切值时要注意利用到角公式.
思路二:根据圆的几何性质圆心一定在弦的垂直平分线上,所以根据两条弦的垂直平分线的交点找出圆心N,然后证明N到四个点A、B、P、Q的距离相等即可.
【解析】(I)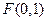 ,
,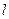 的方程为
的方程为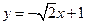 ,代入
,代入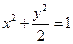 并化简得
并化简得
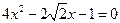 . …………………………2分
. …………………………2分
设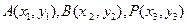 ,
,
则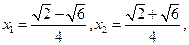
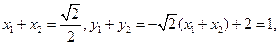
由题意得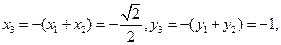
所以点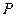 的坐标为
的坐标为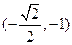 .
.
经验证点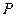 的坐标
的坐标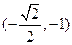 满足方程
满足方程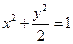 ,故点
,故点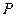 在椭圆
在椭圆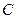 上 …6分
上 …6分
(II)由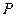
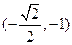 和题设知,
和题设知,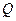
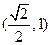 ,
,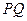 的垂直平分线
的垂直平分线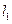 的方程为
的方程为
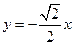 . ①
. ①
设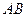 的中点为
的中点为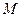 ,则
,则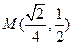 ,
,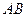 的垂直平分线
的垂直平分线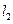 的方程为
的方程为
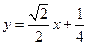 . ②
. ②
由①、②得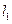 、
、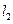 的交点为
的交点为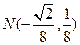 . …………………………9分
. …………………………9分
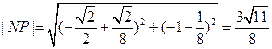 ,
,
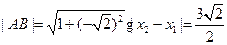 ,
,
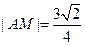 ,
,
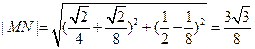 ,
,
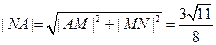 ,
,
故 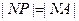 ,
,
又 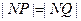 ,
, 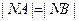 ,
,
所以 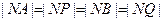 ,
,
由此知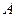 、
、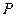 、
、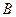 、
、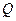 四点在以
四点在以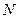 为圆心,
为圆心,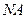 为半径的圆上. ……………12分
为半径的圆上. ……………12分
(II)法二: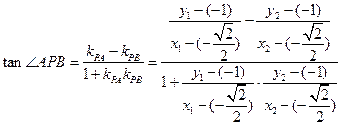
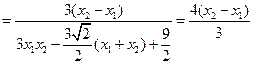
同理
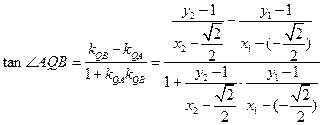
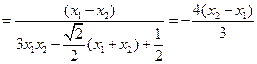
所以 互补,
互补,
因此A、P、B、Q四点在同一圆上。
【点评】本题涉及到平面向量,有一定的综合性和计算量,完成有难度. 首先出题位置和平时模拟几乎没有变化,都保持全卷倒数第二道题的位置,这点考生非常适应的。相对来讲比较容易,是因为这道题最好特点没有任何的未知参数,我们看这道题椭圆完全给出,直线过了椭圆焦点,并且斜率也给出,平时做题斜率不给出,需要通过一定条件求出来,或者根本求不出来,这道题都给了,反而同学不知道怎么下手,让我求什么不知道,给出马上给向量条件,出了两道证明题,这个跟平时做的不太一样,证明题结论给大家,需要大家严谨推导出来,可能叙述的时候有不严谨的地方。这两问出的非常巧妙,非常涉及解析几何本质的内容,一个证明点在椭圆上的问题,还有一个疑问既然出现四点共圆,这都是平时很少涉及内容。从侧面体现教育深层次的问题,让学生掌握解析几何的本质,而不是把套路解决。其实几年前上海考到解析几何本质问题,最后方法用代数方法研究几何的问题,什么是四点共圆?首先在同一个圆上,首先找到圆心,四个点找圆形不好找,最简单的两个点怎么找?这是平时的知识,怎么找距离相等的点,一定在中垂线,两个中垂线交点必然是圆心,找到圆心再距离四个点距离相等,这就是简单的计算问题.方法确定以后计算量其实比往年少.


