(单词翻译:单击)
第Ⅰ卷
一、选择题
(1)复数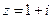 ,
,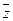 为
为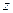 的共轭复数,则
的共轭复数,则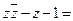
(A)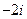 (B)
(B)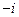 (C)
(C)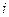 (D)
(D)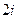
【答案】B
【命题意图】本题主要考查复数的运算.
【解析】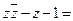 |z|
|z|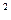
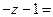 2-(1+i)-1=
2-(1+i)-1=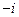 .
.
(2)函数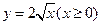 的反函数为
的反函数为
(A)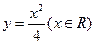 (B)
(B)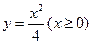
(C)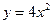
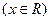 (D)
(D)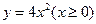
【答案】B
【命题意图】本题主要考查反函数的求法.
【解析】由原函数反解得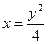 ,又原函数的值域为
,又原函数的值域为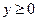 ,所以函数
,所以函数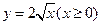 的反函数为
的反函数为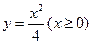 .
.
(3)下面四个条件中,使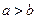 成立的充分而不必要的条件是
成立的充分而不必要的条件是
(A)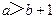 (B)
(B)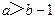 (C)
(C)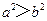 (D)
(D)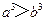
【答案】A
【命题意图】本题主要考查充要条件及不等式的性质.
【解析】即寻找命题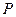 ,使
,使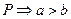 ,且
,且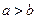 推不出
推不出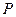 ,逐项验证知可选A.
,逐项验证知可选A.
(4)设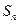 为等差数列
为等差数列
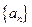 的前
的前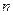 项和,若
项和,若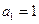 ,公差
,公差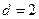 ,
,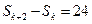 ,则
,则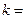
(A)8 (B)7 (C)6 (D)5
【答案】D
【命题意图】本题主要考查等差数列的基本公式的应用.
【解析】解法一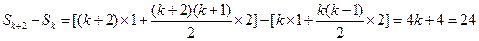 ,解得
,解得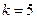 .
.
解法二: 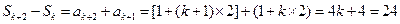 ,解得
,解得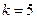 .
.
(5)设函数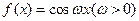 ,将
,将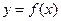 的图像向右平移
的图像向右平移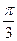 个单位长度后,所得的图像与原图像重合,则
个单位长度后,所得的图像与原图像重合,则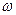 的最小值等于
的最小值等于
(A)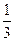 (B)
(B)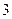 (C)
(C)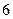 (D)
(D)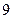
【答案】C
【命题意图】本题主要考查三角函数的周期性及三角函数图像的平移变换.
【解析】由题意得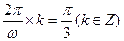 ,解得
,解得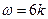 ,又
,又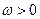 ,令
,令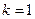 ,得
,得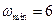 .
.
(6)已知直二面角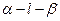 ,点
,点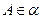 ,
,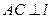 ,
,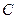 为垂足,
为垂足,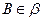 ,
,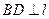 ,
,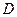 为垂
为垂
足.若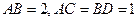 ,则
,则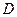 到平面
到平面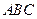 的距离等于
的距离等于
(A)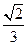 (B)
(B)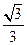 (C)
(C)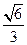 (D) 1
(D) 1
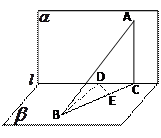
【答案】C
【命题意图】本题主要考查空间点到平面距离的求法.
【解析】如图,过 作
作 ,垂足为
,垂足为 ,因为
,因为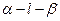 是直二面角,
是直二面角, 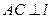 ,∴
,∴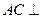 平面
平面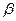 ,
,
∴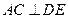 ,
,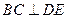 ,
,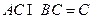 ,∴
,∴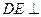 平面
平面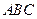 ,故
,故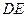 的长为点
的长为点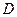 到平面
到平面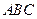 的距离.在
的距离.在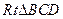 中,由等面积法得
中,由等面积法得 .
.
(7)某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友每位朋友1本,则不同的赠送方法共有
(A)4种 (B)10种 (C)18种 (D)20种
【答案】B
【命题意图】本题主要考查两个原理与排列组合知识,考察考生分析问题的能力.
【解析】分两类:一是取出1本画册,3本集邮册,此时赠送方法有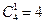 种;
种;
二是取出2本画册,2本集邮册,此时赠送方法有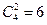 种.故赠送方法共有10
种.故赠送方法共有10 种.
种.
(8)曲线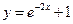 在点(0,2)处的切线与直线
在点(0,2)处的切线与直线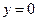 和
和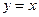 围
围 成的三角形的面积为
成的三角形的面积为
(A)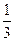 (B)
(B)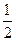 (C)
(C)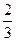 (D)1
(D)1
【答案】A
【命题意图】本题主要考查利用导数求切线方程和三角形面积公式.
【解析】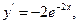 ∴曲线
∴曲线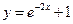 在点(0,2)处的切线的斜率
在点(0,2)处的切线的斜率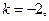 故切线方程是
故切线方程是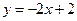 ,在直角坐标系中作出示意图得围
,在直角坐标系中作出示意图得围 成的三角形的三个顶点分别为(0,0)、(1,0)、(
成的三角形的三个顶点分别为(0,0)、(1,0)、(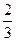 ,
, 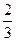 ),∴三角形的面积是
),∴三角形的面积是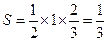 .
.
(9)设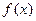 是周期为2的奇函数,当
是周期为2的奇函数,当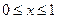 时,
时,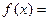
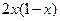 ,则
,则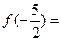
(A) -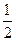 (B)
(B)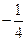 (C)
(C)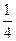 (D)
(D)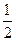
【答案】A
【命题意图】本题主要考查利用函数的周期性和奇偶性求函数值的方法.
【解析】由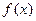 是周期为2的奇函数,利用周期性和奇偶性得:
是周期为2的奇函数,利用周期性和奇偶性得: 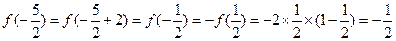 .
.
(10)已知抛物线C: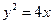 的焦点为
的焦点为 ,直线
,直线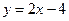 与
与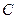 交于
交于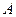 ,
,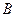 两点.则
两点.则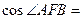
(A)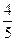 (B)
(B)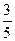 (C)
(C)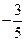 (D)
(D)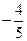
【答案】D
【命题意图】本题主要考查直线与抛物线的位置关系,余弦定理的应用.
【解析】联立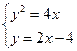 消去
消去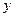 得
得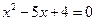 ,解得
,解得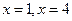 ,不妨设
,不妨设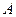 点在
点在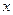 轴的上方,于是
轴的上方,于是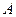 ,
,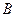 两点的坐标分别为(4,4),(1,
两点的坐标分别为(4,4),(1,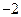 ),又
),又 ,可求得
,可求得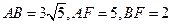 .在
.在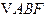 中,由余弦定理
中,由余弦定理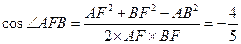 .
.
(11)已知平面α截一球面得圆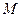 ,过圆心
,过圆心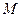 且与α成
且与α成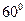 二面角的平面β截该球面得圆
二面角的平面β截该球面得圆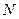 .若该球面的半径为4,圆
.若该球面的半径为4,圆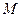 的面积为4
的面积为4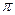 ,则圆
,则圆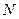 的面积为
的面积为
(A)7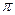 (B)9
(B)9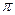 (C)11
(C)11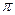 (D)13
(D)13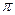
【答案】D
【命题意图】本题主要考查二面角的概念与球的性质.
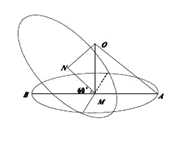
【解析】如图所示,由圆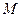 的面积为4
的面积为4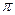 知球心
知球心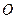 到圆
到圆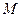 的距离
的距离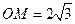 ,在
,在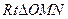 中,
中,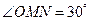 , ∴
, ∴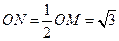 ,故圆
,故圆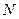 的半径
的半径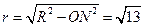 ,∴圆
,∴圆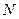 的面积为
的面积为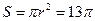 .
.
(12)设向量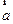 ,
,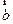 ,
,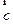 满足|
满足|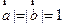 ,
,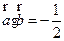 ,
,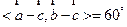 ,则
,则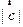 的最大值等于
的最大值等于
(A)2 (B)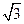
 (c)
(c)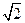 (D)1
(D)1
【答案】A
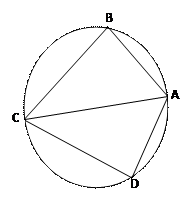
【命题意图】本题主要考查平面向量的数量积运算、向量加减法、四点共圆的条件及数形结合的思想.
【解析】如图,设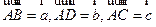 ,则
,则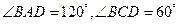 ,
,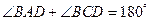 ,∴
,∴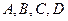 四点共圆,当
四点共圆,当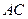 为圆的直径时,
为圆的直径时,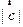 最大,最大值为2.
最大,最大值为2.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上(注意:在试卷上作答无效)
(13)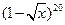 的二项展开式中,
的二项展开式中,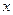 的系数与
的系数与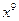 的系数之差为
的系数之差为  .
.
【答案】0
【命题意图】本题主要考查二项展开式的通项公式和组合数的性质.
【解析】由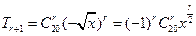 得
得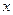 的系数为
的系数为 ,
,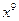 的系数为
的系数为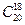 ,而
,而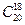 =
= ,所以
,所以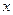 的系数与
的系数与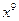 的系数之差为0.
的系数之差为0.
(14)已知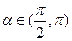 ,
,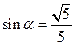 ,则
,则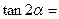
 .
.
【答案】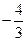
【命题意图】本题主要考查同角三角函数的基本关系和二倍角的正切公式.
【解析】由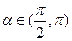 ,
,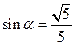 得
得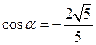 ,故
,故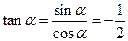 ,
,
∴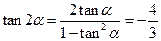 .
.
(15)已知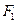 、
、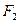 分别为双曲线
分别为双曲线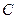 :
: 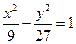 的左、右焦点,点
的左、右焦点,点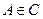 ,点
,点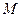 的坐标为(2,0),
的坐标为(2,0),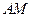 为
为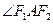 的平分线.则
的平分线.则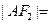 .
.
【答案】6
【命题意图】本题主要考查三角形的内角平分线定理,双曲线的第一定义和性质.
【解析】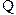
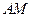 为
为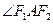 的平分线,∴
的平分线,∴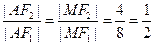 ∴
∴
又点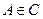 ,由双曲线的第一定义得
,由双曲线的第一定义得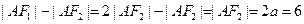 .
.
(16)己知点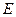 、
、 分别在正方体
分别在正方体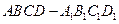 的棱
的棱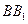 、
、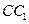 上,且
上,且 ,则面
,则面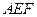 与面
与面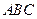 所成的二面角的正切值等于 .
所成的二面角的正切值等于 .
【答案】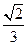
【命题意图】本题主要考查正方体中二面角的求法.
【解析】延长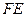 交
交 的延长线于
的延长线于 ,连结
,连结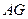 ,则
,则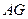 为面
为面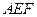 与面
与面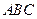 的交线,由
的交线,由 得
得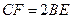 ,∴
,∴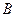 为
为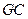 中点.设正方体的棱长为1,则
中点.设正方体的棱长为1,则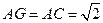 ,又
,又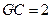 ,∴
,∴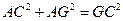 ∴
∴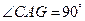
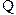
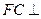 平面
平面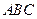 ,∴
,∴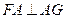 ∴
∴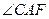 是面
是面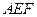 与面
与面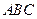 所成的二面角的平面角,在
所成的二面角的平面角,在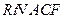 中,
中,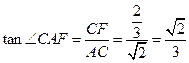 ,故面
,故面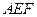 与面
与面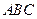 所成的二面角的正切值等于
所成的二面角的正切值等于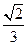 .
.
三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分l0分)(注意:在试题卷上作答无效)
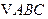 的内角
的内角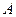 、
、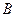 、
、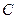 的对边分别为
的对边分别为 、
、 、
、 .已知
.已知 , ,求
, ,求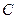 .
.

【命题意图】本题主要考查正弦定理、三角形内角和定理、诱导公式、辅助角公式,考查考生对基础知识、基本技能的掌握情况.
【解析】由 及正弦定理可得
及正弦定理可得
 …………………………………3分
…………………………………3分
又由 ,
,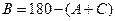 ,故
,故
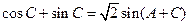
=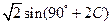
=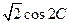 …………………………………7分
…………………………………7分
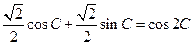 ,
,
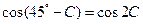
因为  ,
,
所以  ,
,
 …………………………………10分
…………………………………10分
【点评】三角函数与解三角形的综合性问题,是近几年高考的热点,在高考试题中频繁出现.这类题型难度比较低,一般出现在17或18题,属于送分题,估计以后这类题型仍会保留,不会有太大改变.解决此类问题,要根据已知条件,灵活运用正弦定理或余弦定理,求边角或将边角互化.
(18)(本小题满分l2分)(注意:在试题卷上作答无效)
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲 种保险的概率为0.3,设各车主购买保险相互独立.
种保险的概率为0.3,设各车主购买保险相互独立.
(I)求该地1位车主至少购买甲、乙两种保险中的l种的概率;
(Ⅱ)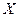 表示该地的l00位车主中,甲、乙两种保险都不购买的车主数.求
表示该地的l00位车主中,甲、乙两种保险都不购买的车主数.求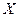 的期望.
的期望.
【命题意图】本题主要考查独立事件的概率、对立事件的概率、互斥事件的概率及二项分布的数学期望,考查考生分析问题、解决问题的能力.
【解析】记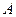 表示事件: 该地的1位车主购买甲种保险;
表示事件: 该地的1位车主购买甲种保险;
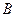 表示事件: 该地的1位车主购买乙种保险但不购买甲
表示事件: 该地的1位车主购买乙种保险但不购买甲 种保险;
种保险;
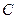 表示事件: 该地的1位车主至少购买甲、乙两种保险中的l种;
表示事件: 该地的1位车主至少购买甲、乙两种保险中的l种;
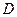 表示事件: 该地的1位车主甲、乙两种保险都不购买.
表示事件: 该地的1位车主甲、乙两种保险都不购买.
(I) ,
, 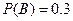 ,
,  ……………………………3分
……………………………3分
 ……………………………6分
……………………………6分
(Ⅱ) ,
,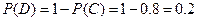
 ,即
,即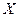 服从二项分布, ……………………………10分
服从二项分布, ……………………………10分
所以期望  . ……………………………12分
. ……………………………12分
【点评】概率与统计是每年的必考题,一般安排在解答题的前3题.本题属于已知概率求概率类型. 考查保险背景下的概率问题,要求考生熟练掌握独立事件的概率、对立事件的概率、互斥事件的概率及二项分布的数学期望.
(19)(本小题满分l2分)(注意:在试题卷上作答无效)
如图,四棱锥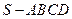 中,
中, 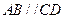 ,
,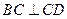 ,侧面
,侧面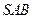 为等边三角形,
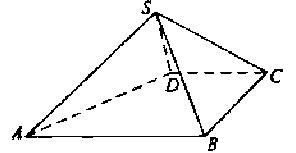
为等边三角形,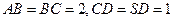 .
.
(Ⅰ)证明: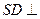 平面
平面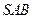 ;
;
(Ⅱ)求 与平面
与平面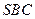 所成角的大小.
所成角的大小.
【命题意图】以四棱锥为载体考查线面垂直证明和线面角的计算,注重与平面几何的综合.
解法一:(Ⅰ)取 中点
中点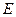 ,连结
,连结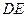 ,则四边形
,则四边形 为矩形,
为矩形, ,连结
,连结 ,则
,则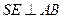 ,
,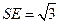 .
.
又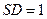 ,故
,故 ,所以
,所以 为直角. ………………3分
为直角. ………………3分
由 ,
, ,
, ,得
,得 平面
平面 ,所以
,所以 .
.
 与两条相交直线
与两条相交直线 、
、 都垂直.
都垂直.
所以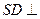 平面
平面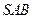 . ………………6分
. ………………6分
另解:由已知易求得 ,于是
,于是 .可知
.可知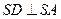 ,同理可得
,同理可得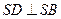 ,又
,又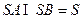 .所以
.所以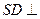 平面
平面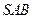 . ………………6分
. ………………6分
(Ⅱ)由 平面
平面 知,平面
知,平面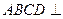 平面
平面 .
.
作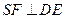 ,垂足为
,垂足为 ,则
,则 平面ABCD,
平面ABCD, .
.
作 ,垂足为
,垂足为 ,则
,则 .
.
连结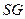 .则
.则 .
.
又 ,故
,故 平面
平面 ,平面
,平面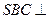 平面
平面 .……9分
.……9分
作 ,
, 为垂足,则
为垂足,则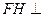 平面
平面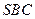 .
.
 ,即
,即 到平面
到平面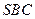 的距离为
的距离为 .
.
由于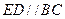 ,所以
,所以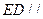 平面
平面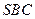 ,
,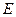 到平面
到平面 的距离
的距离 也为
也为 .
.
设 与平面
与平面 所成的角为
所成的角为 ,则
,则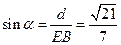 ,
, .……12分
.……12分
解法二:以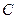 为原点,射线
为原点,射线 为
为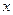 轴的正半轴,建立如图所示的空间直角坐标系
轴的正半轴,建立如图所示的空间直角坐标系 .
.
设 ,则
,则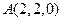 、
、 .
.
又设 ,则
,则 .
.
(Ⅰ) ,
,
由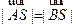 得
得
 ,
,
故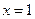 .
.
由 得
得 ,
,
又由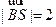 得
得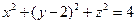 ,
,
即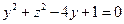 ,故
,故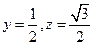 . ………………3分
. ………………3分
于是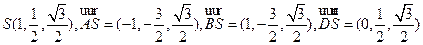 ,
,
 .
.
故 ,又
,又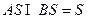 ,
,
所以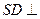 平面
平面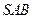 . ………………6分
. ………………6分
(Ⅱ)设平面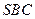 的法向量
的法向量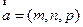 ,
,
则 .
.
又 ,
,
故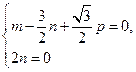 ………………9分
………………9分
取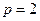 得
得 ,又
,又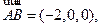
 .
.
故 与平面
与平面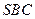 所成的角为
所成的角为 . ………………12分
. ………………12分
【点评】立体几何一直以来都是让广大考生又喜又忧的题目.为之而喜是因为只要能建立直角坐标系,基本上可以处理立体几何绝大多数的问题;为之而忧就是对于不规则的图形来讲建系的难度较大,问题不能得到很好的解决.今年的立几问题建系就存在这样的问题,很多考生由于建系问题导致立几的完成情况不是很好.
(20)(本小题满分l2分)(注意:在试题卷上作答无效)
设数列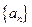 满足
满足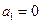 且
且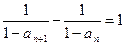 .
.
求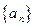 的通项公式;
的通项公式;
(Ⅱ)设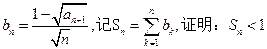 .
.
【命题意图】本题主要考查等差数列的定义及其通项公式,裂项相消法求和,不等式的证明,考查考生分析问题、解决问题的能力.
【解析】(Ⅰ)由题设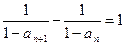 ,
,
即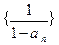 是公差为1的等差数列.
是公差为1的等差数列.
又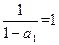 ,故
,故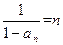 .
.
所以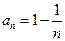 ……………………………5分# (Ⅱ) 由(Ⅰ)得
……………………………5分# (Ⅱ) 由(Ⅰ)得
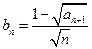
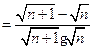
 ,
,
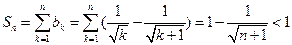 …………………………12分
…………………………12分
【点评】2011年高考数学全国卷将数列题由去年的第18题后移,一改往年的将数列结合不等式放缩法问题作为押轴题的命题模式,具有让考生和一线教师重视教材和基础知识、基本方法基本技能,重视两纲的导向作用,也可看出命题人在有意识降低难度和求变的良苦用心.估计以后的高考,对数列的考查主要涉及数列的基本公式、基本性质、递推数列、数列求和、数列极限、简单的数列不等式证明等,这种考查方式还要持续.
(21)(本小题满分l2分)(注意:在试题卷上作答无效)
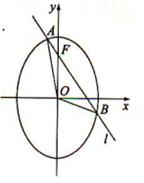
已知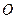 为坐标原点,
为坐标原点, 为椭圆
为椭圆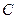 :
: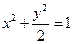 在
在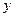 轴正半轴上的焦点,过
轴正半轴上的焦点,过 且斜率为
且斜率为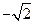 的直线
的直线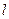 与
与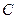 交与
交与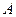 、
、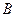 两点,点
两点,点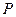 满
满 足
足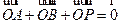 .
.
(I)证明:点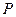 在
在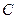 上;
上;
(II)设点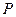 关于点
关于点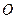 的对称点为
的对称点为 ,证明:
,证明: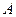 、
、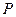 、
、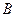 、
、 四点在同一圆上.
四点在同一圆上.
【命题意图】本题考查直线方程、平面向量的坐标运算、点与曲线的位置关系、曲线交点坐标求法及四点共圆的条件。
【解析】(I)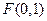 ,
,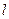 的方程为
的方程为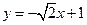 ,代入
,代入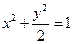 并化简得
并化简得
 . …………………………2分
. …………………………2分
设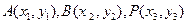 ,
,
则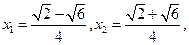

由题意得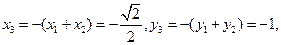
所以点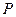 的坐标为
的坐标为 .
.
经验证点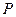 的坐标
的坐标 满足方程
满足方程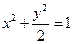 ,故点
,故点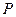 在椭圆
在椭圆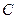 上 …6分
上 …6分
(II)由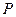
 和题设知,
和题设知,
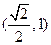 ,
,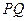 的垂直平分线
的垂直平分线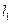 的方程为
的方程为
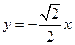 . ①
. ①
设 的中点为
的中点为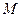 ,则
,则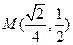 ,
, 的垂直平分线
的垂直平分线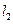 的方程为
的方程为
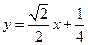 . ②
. ②
由①、②得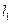 、
、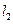 的交点为
的交点为 . …………………………9分
. …………………………9分
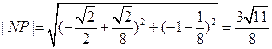 ,
,
 ,
,
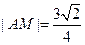 ,
,
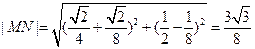 ,
,
 ,
,
故  ,
,
又 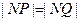 ,
,  ,
,
所以 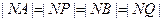 ,
,
由此知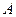 、
、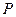 、
、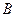 、
、 四点在以
四点在以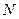 为圆心,
为圆心,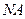 为半径的圆上. ……………12分
为半径的圆上. ……………12分
【点评】本题涉及到平面微向量,有一定的综合性和计算量,完成有难度. 首先出题位置和平时模拟几乎没有变化,都保持全卷倒数第二道题的位置,这点考生非常适应的。相对来讲比较容易,是因为这道题最好特点没有任何的未知参数,我们看这道题椭圆完全给出,直线过了椭圆焦点,并且斜率也给出,平时做题斜率不给出,需要通过一定条件求出来,或者根本求不出来,这道题都给了,反而同学不知道怎么下手,让我求什么不知道,给出马上给向量条件,出了两道证明题,这个跟平时做的不太一样,证明题结论给大家,需要大家严谨推导出来,可能叙述的时候有不严谨的地方。这两问出的非常巧妙,非常涉及解析几何本质的内容,一个证明点在椭圆上的问题,还有一个疑问既然出现四点共圆,这都是平时很少涉及内容。从侧面体现教育深层次的问题,让学生掌握解析几何的本质,而不是把套路解决。其实几年前上海考到解析几何本质问题,最后方法用代数方法研究几何的问题,什么是四点共圆?首先在同一个圆上,首先找到圆心,四个点找圆形不好找,最简单的两个点怎么找?这是平时的知识,怎么找距离相等的点,一定在中垂线,两个中垂线交点必然是圆心,找到圆心再距离四个点距离相等,这就是简单的计算问题。方法确定以后计算量其实比往年少.
(22)(本小题满分l2分)(注意:在试题卷上作答无效)
(I)设函数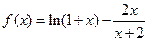 ,证明:当
,证明:当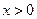 时,
时,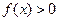 ;
;
(II)从编号1到100的100张卡片中每次随即抽取一张,然后放回,用这种方式 连续抽取20次,设抽得的20个号码互不相同的概率为
连续抽取20次,设抽得的20个号码互不相同的概率为 .证
.证 明:
明: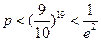
【命题意图】本题为导数、概率与不等式的综合,主要考查导数的应用和利用导数证明不等式.考查考生综合运用知识的能力及分类讨论的思想,考查考生的计算能力及分析问题、解决问题的能力.
【解析】(I)  …………………………2分
…………………………2分
当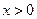 时,
时,  ,所以
,所以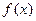 为增函数,又
为增函数,又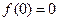 ,因此当
,因此当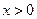 时,
时,
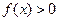 . …………………………5分
. …………………………5分
(II) 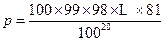 .
.
又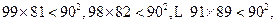
所以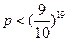 .
.
由(I)知: 当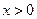 时,
时, 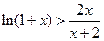
因此 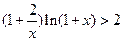 .
.
在上式中,令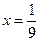 ,则 19
,则 19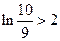 ,即
,即 .
.
所以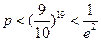 …………………………12分
…………………………12分
【点评】导数常作为高考的压轴题,对考生的能力要求非常高,它不仅要求考生牢固掌握基础知识、基本技能,还要求考生具有较强的分析能力和计算能力 .估计以后对导数的考查力度不会减弱.作为压轴题,主要是涉及利用导数求最值解决恒成立问题,利用导数证明不等式等,有时还伴随对参数的讨论,这也是难点之所在.
.估计以后对导数的考查力度不会减弱.作为压轴题,主要是涉及利用导数求最值解决恒成立问题,利用导数证明不等式等,有时还伴随对参数的讨论,这也是难点之所在.


