(单词翻译:单击)
第一部分(选择题 共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目的要求的.
1.若全集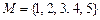 ,
,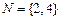 ,则
,则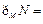
(A)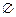 (B)
(B)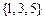 (C)
(C)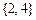 (D)
(D)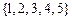
答案:B
解析:∵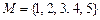 ,则
,则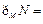
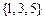 ,选B.
,选B.
2.有一个容量为66的样本,数据的分组及各组的频数如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9 [23.5,27.5) 18
[27.5,31.5) 1l [31.5,35.5) 12 [35.5,39.5) 7 [39.5,43.5) 3
根据样本的频率分布估计,大于或等于31.5的数据约占
(A)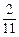 (B)
(B) 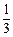 (C)
(C)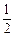 (D)
(D)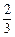
答案:B
解析:大于或等于31.5的数据共有12+7+3=22个,约占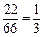 ,选B.
,选B.
3.圆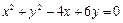 的圆心坐标是
的圆心坐标是
(A)(2,3) (B)(-2,3) (C)(-2,-3) (D)(2,-3)
答案:D
解析:圆方程化为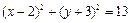 ,圆心(2,-3),选D.
,圆心(2,-3),选D.
4.函数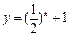 的图象关于直线y=x对称的图象像大致是
的图象关于直线y=x对称的图象像大致是
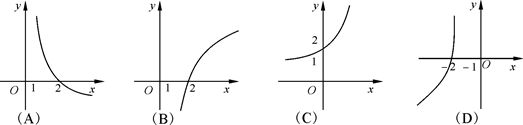
答案:A
解析: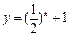 图象过点
图象过点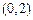 ,且单调递减,故它关于直线y=x对称的图象过点
,且单调递减,故它关于直线y=x对称的图象过点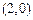 且单调递减,选A.
且单调递减,选A.
5.“x=3”是“x2=9”的
(A)充分而不必要的条件 (B)必要而不充分的条件
(C)充要条件 (D)既不充分也不必要的条件
答案:A
解析:若x=3,则x 2=9,反之,若x 2=9,则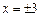 ,选A.
,选A.
6.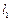 ,
,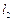 ,
,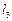 是空间三条不同的直线,则下列命题正确的是
是空间三条不同的直线,则下列命题正确的是
(A)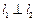 ,
,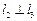
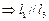 (B)
(B)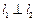 ,
,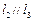
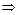
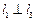
(C)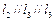
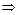
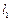 ,
,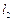 ,
,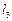 共面 (D)
共面 (D)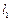 ,
,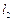 ,
,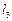 共点
共点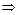
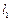 ,
,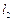 ,
,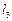 共面
共面
答案:B
解析:由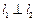 ,
,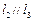 ,根据异面直线所成角知
,根据异面直线所成角知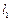 与
与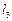 所成角为90°,选B.
所成角为90°,选B.
7.如图,正六边形ABCDEF中,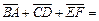
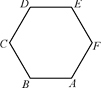
(A)0 (B)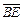
(C)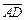 (D)
(D)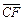
答案:D
解析: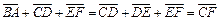 ,选D.
,选D.
8.在△ABC中,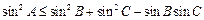 ,则A的取值范围是
,则A的取值范围是
(A)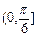 (B)
(B)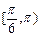 (C)
(C)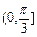 (D)
(D)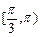
答案:C
解析:由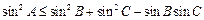 得
得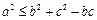 ,即
,即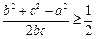 ,
,
∴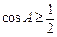 ,∵
,∵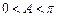 ,故
,故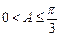 ,选C.
,选C.
9.数列{an}的前n项和为Sn,若a1=1,an+1 =3Sn(n ≥1),则a6=
(A)3 × 44 (B)3 × 44+1 (C)44 (D)44+1
答案:A
解析:由an+1 =3Sn,得an =3Sn-1(n ≥ 2),相减得an+1-an =3(Sn-Sn-1)= 3an,则an+1=4an(n ≥ 2),a1=1,a2=3,则a6= a2·44=3×44,选A.
10.某运输公司有12名驾驶员和19名工人,有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需运往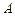 地至
地至 少72吨的货
少72吨的货 物,派用的每辆车需满载且只运送一次.派用的每辆甲型卡车需配2名工人,运送一次可得利润450元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元,该公司合理计划当天派用两类卡车的车辆数,可得最大利润为
物,派用的每辆车需满载且只运送一次.派用的每辆甲型卡车需配2名工人,运送一次可得利润450元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元,该公司合理计划当天派用两类卡车的车辆数,可得最大利润为
(A)4650元 (B)4700元 (C)4900元 (D)5000元
答案:C
解析:设派用甲型卡车x(辆),乙型卡车y(辆),获得的利润为u(元),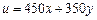 ,由题意,x、y满足关系式
,由题意,x、y满足关系式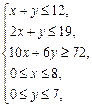 作出相应的平面区域,
作出相应的平面区域,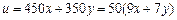 在由
在由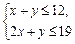 确定的交点
确定的交点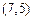 处取得最大值4900元,选C.
处取得最大值4900元,选C.
11.在抛物线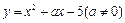 上取横坐标为
上取横坐标为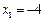 ,
,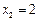 的两点,过这两点引一条割线,有平行于该割线的一条直线同时与抛物线和圆
的两点,过这两点引一条割线,有平行于该割线的一条直线同时与抛物线和圆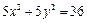 相切,则抛物线顶点的坐标为
相切,则抛物线顶点的坐标为
(A)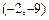 (B)
(B)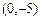 (C)
(C)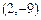 (D)
(D)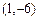
答案:A
解析:令抛物线上横坐标为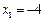 、
、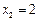 的点为
的点为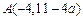 、
、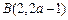 ,则
,则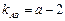 ,由
,由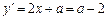 ,故切点为
,故切点为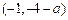 ,切线方程为
,切线方程为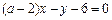 ,该直线又和圆相切,则
,该直线又和圆相切,则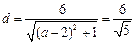 ,解得
,解得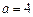 或
或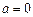 (舍去),则抛物线为
(舍去),则抛物线为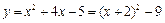 ,定点坐标为
,定点坐标为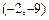 ,选A.
,选A.
12.在集合 中任取一个偶数a和一个奇数b构成以原点为起点的向量
中任取一个偶数a和一个奇数b构成以原点为起点的向量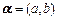 ,从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为n,其中面积等于2的平行四边形的个数为
,从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为n,其中面积等于2的平行四边形的个数为 m,则
m,则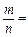
(A)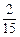 (B)
(B)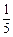 (
( C)
C)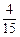 (D)
(D)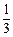
答案:B
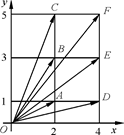
解析:∵以原点为起点的向量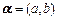 有
有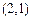 、
、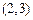 、
、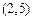 、
、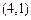 、
、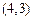 、
、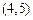 共6个,可作平行四边形的个数
共6个,可作平行四边形的个数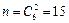 个,结合图形进行计算,其中由
个,结合图形进行计算,其中由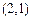
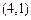 、
、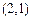
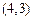 、
、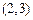
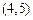 确定的平行四边形面积为2,共有3个,则
确定的平行四边形面积为2,共有3个,则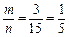 ,选B.
,选B.
第二部分(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.
13.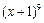 的展开式中
的展开式中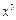 的系数是_________.(用数字作答)
的系数是_________.(用数字作答)
答案:84
解析:∵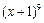 的展开式中
的展开式中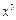 的系数是
的系数是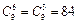 .
.
14.双曲线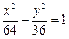 上一点P到双曲线右焦点的距离是4,那么P到左准线的距离是____.
上一点P到双曲线右焦点的距离是4,那么P到左准线的距离是____.
答案:16
答案:16
解析:离心率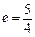 ,设P到右准线的距离是d,则
,设P到右准线的距离是d,则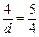 ,则
,则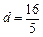 ,则P到左准线的距离等于
,则P到左准线的距离等于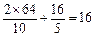 .
.
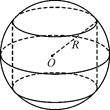
15.如图,半径为4的球O中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是_________.
答案:32π
解析:如图,设球一条半径与圆柱相应的母线夹角为α,圆柱侧面积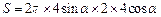 =
=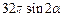 ,当
,当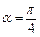 时,S取最大值
时,S取最大值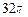 ,此时球的表面积与该圆柱的侧面积之差为
,此时球的表面积与该圆柱的侧面积之差为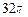 .
.
16.函数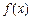 的定义域为A,若
的定义域为A,若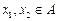 且
且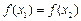 时总有
时总有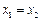 ,则称
,则称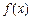 为单函数.例如,函数
为单函数.例如,函数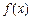 =2x+1(
=2x+1(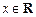 )是单函数.下列命题:
)是单函数.下列命题:
①函数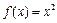 (x
(x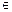 R)是单函数;
R)是单函数;
②指数函数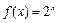 (x
(x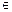 R)是单函数;
R)是单函数;
③若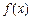 为单函数,
为单函数,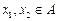 且
且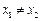 ,则
,则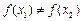 ;
;
④在定义域上具有单调性的函数一定是单函数.
其中的真命题是_________.(写出所有真命题的编号)
答案:②③④
解析:对于①,若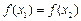 ,则
,则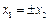 ,不满足;②是单函数;命题③实际上是单函数命题的逆否命题,故为真命题;根据定义,命题④满足条件.
,不满足;②是单函数;命题③实际上是单函数命题的逆否命题,故为真命题;根据定义,命题④满足条件.
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题共l2分)
本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租车不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算).有甲、乙人互相独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为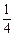 、
、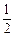 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为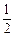 、
、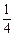 ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(Ⅰ)分别 求出甲、乙在三小时以上且不超过四小时还车的概率;
求出甲、乙在三小时以上且不超过四小时还车的概率;
(Ⅱ)求甲、乙两人所付的租车费用之和小于6元的概率.
本小题主要考查相互独立事件、互斥事件等概念及相关概率计算,考查运用所学知识和方法解决实际问题的能力.
解:(Ⅰ)分别记甲、乙在三小时以上且不超过四小时还车为事件A、B,则
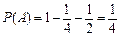 ,
,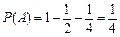 .
.
答:甲、乙在三小时以上且不超过四小时还车的概率分别为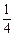 、
、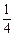 .
.
(Ⅱ)记甲、乙两人所付的租车费用之和小于6元为事件C,则
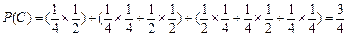 .
.
答:甲、乙两人所付的租车费用之和小于6元的概率为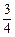
18.(本小题共l2分)
已知函数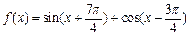 ,x
,x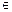 R.
R.
(Ⅰ)求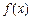 的最小正周期和最小值;
的最小正周期和最小值;
(Ⅱ)已知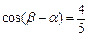 ,
,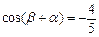 ,
,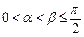 .求证:
.求证: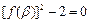 .
.
本小题考查三角函数的性质,同角三角函数的关系,两角和的正、余弦公式、诱导公式等基础知识和基本运算能力,函数与方程、化归与转化等数学思想.
(Ⅰ)解析: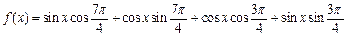
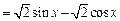
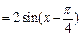 ,∴
,∴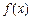 的最小正周期
的最小正周期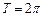 ,最小值
,最小值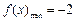 .
.
(Ⅱ)证明:由已知得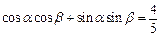 ,
,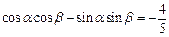
两式相加得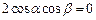 ,∵
,∵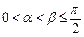 ,∴
,∴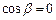 ,则
,则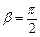 .
.
∴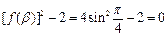 .
.
19.(本小题共l2分)
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D.
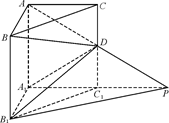
(Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值;
本小题主要考查直三棱柱的性质、线面关系、二面角等基本知识,并考查空间想象能力和逻辑推理能力,考查应用向量知识解决问题的能力.
解法一:
(Ⅰ)连结AB1与BA1交于点O,连结OD,
∵C1D∥平面AA1,A1C1∥AP,∴AD=PD,又AO=B1O,
∴OD∥PB1,又ODÌ面BDA1,PB1Ë面BDA1,
∴PB1∥平面BDA1.
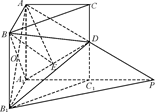
(Ⅱ)过A作AE⊥DA1于点E,连结BE.∵BA⊥CA,BA⊥AA1,且AA1∩AC=A,
∴BA⊥平面AA1C1C.由三垂线定理可知BE⊥DA1.
∴∠BEA为二面角A-A1D-B的平面角.
在Rt△A1C1D中,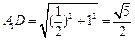 ,
,
又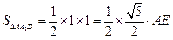 ,∴
,∴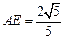 .
.
在Rt△BAE中,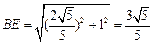 ,∴
,∴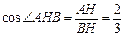 .
.
故二面角A-A1D-B的平面角的余弦值为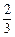 .
.
解法二:
如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系A1-B1C1A,则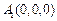 ,
,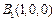 ,
,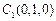 ,
,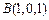 ,
,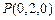 .
.
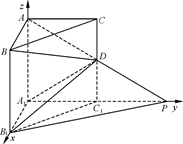
(Ⅰ)在△PAA1中有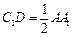 ,即
,即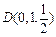 .
.
∴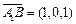 ,
,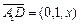 ,
,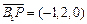 .
.
设平面BA1D的一个法向量为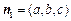 ,
,
则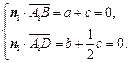 令
令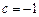 ,则
,则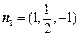 .
.
∵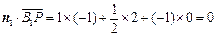 ,
,
∴PB1∥平面BA1D,
(Ⅱ)由(Ⅰ)知,平面BA1D的一个法向量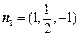 .
.
又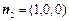 为平面AA1D的一个法向量.∴
为平面AA1D的一个法向量.∴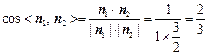 .
.
故二面角A-A1D-B的平面角的余弦值为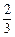 .
.
20.(本小题共12分)
已知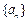 是以a为首项,q为公比的等比数列,
是以a为首项,q为公比的等比数列,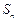 为它的前n项和.
为它的前n项和.
(Ⅰ)当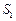 、
、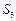 、
、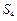 成等差数列时,求q的值;
成等差数列时,求q的值;
(Ⅱ)当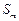 、
、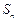 、
、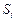 成等差数列时,求证:对任意自然数k,
成等差数列时,求证:对任意自然数k,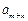 、
、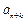 、
、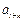 也成等差数列.
也成等差数列.
本小题考查等比数列和等差数列的基础知识以及基本运算能力和分析问题、解决问题的能力.
解:(Ⅰ)由已知,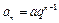 ,因此
,因此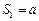 ,
, ,
,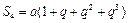 .
.
当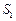 、
、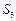 、
、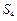 成等差数列时,
成等差数列时,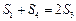 ,可得
,可得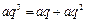 .
.
化简得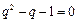 .解得
.解得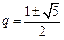 .
.
(Ⅱ)若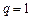 ,则
,则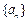 的每项
的每项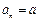 ,此时
,此时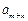 、
、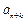 、
、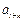 显然成等差数列.
显然成等差数列.
若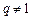 ,由
,由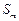 、
、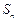 、
、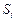 成等差数列可得
成等差数列可得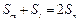 ,即
,即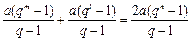 .
.
整理得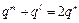 .因此,
.因此,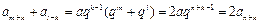 .
.
所以,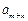 、
、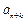 、
、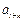 也成等差数列.
也成等差数列.
21.(本小题共l2分)
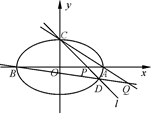
过点C(0,1)的椭圆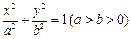 的离心率为
的离心率为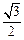 ,椭圆与x轴交于两点
,椭圆与x轴交于两点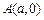 、
、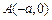 ,过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
,过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
(I)当直线l过椭圆右焦点时,求线段CD的长;
(Ⅱ)当点P异于点B时,求证: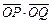 为定值.
为定值.
本小题主要考查直线、椭圆的标准方程及基本性质等基本知识,考查平面解析几何的思想方法及推理运算能力.
解:(Ⅰ)由已知得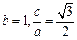 ,解得
,解得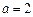 ,所以椭圆方程为
,所以椭圆方程为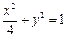 .
.
椭圆的右焦点为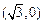 ,此时直线
,此时直线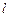 的方程为
的方程为 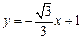 ,代入椭圆方程得
,代入椭圆方程得
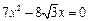 ,解得
,解得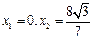 ,代入直线
,代入直线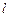 的方程得
的方程得 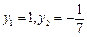 ,所以
,所以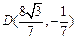 ,
,
故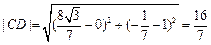 .
.
(Ⅱ)当直线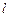 与
与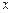 轴垂直时与题意不符.
轴垂直时与题意不符.
设直线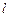 的方程为
的方程为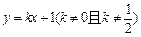 .代入椭圆方程得
.代入椭圆方程得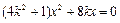 .
.
解得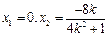 ,代入直线
,代入直线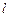 的方程得
的方程得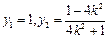 ,
,
所以D点的坐标为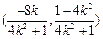 .
.
又直线AC的方程为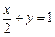 ,又直线BD的方程为
,又直线BD的方程为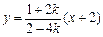 ,联立得
,联立得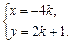
因此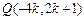 ,又
,又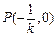 .
.
所以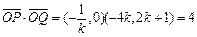 .
.
故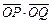 为定值.
为定值.
22.(本小题共l4分)
已知 函数
函数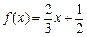 ,
,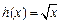 .
.
(Ⅰ)设函数F(x)=18f(x)-x2[h(x)]2,求F(x)的单调区间与极值;
(Ⅱ)设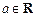 ,解关于x的方程
,解关于x的方程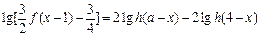 ;
;
(Ⅲ)设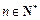 ,证明:
,证明: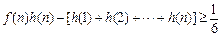 .
.
本小题主要考查函数导数的应用、不等式的证明、解方程等基础知识,考查数形结合、函数与方程、分类与整合等数学思想方法及推理运算、分析问题、解决问题的能力.
解:(Ⅰ)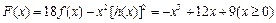 ,
,
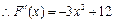 .
.
令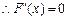 ,得
,得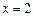 (
(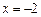 舍去).
舍去).
当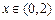 时.
时.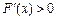 ;当
;当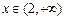 时,
时,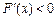 ,
,
故当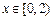 时,
时,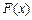 为增函数;当
为增函数;当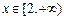 时,
时,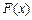 为减函数.
为减函数.
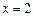 为
为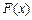 的极大值点,且
的极大值点,且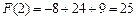 .
.
(Ⅱ)方法一:原方程可化为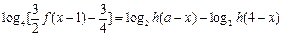 ,
,
即为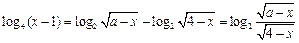 ,且
,且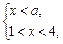
①当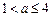 时,
时,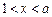 ,则
,则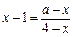 ,即
,即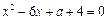 ,
,
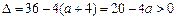 ,此时
,此时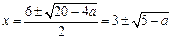 ,∵
,∵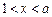 ,
,
此时方程仅有一解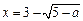 .
.
②当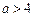 时,
时,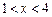 ,由
,由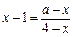 ,得
,得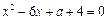 ,
,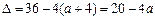 ,
,
若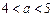 ,则
,则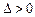 ,方程有两解
,方程有两解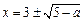 ;
;
若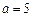 时,则
时,则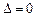 ,方程有一解
,方程有一解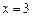 ;
;
若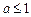 或
或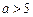 ,原方程无解.
,原方程无解.
方法二:原方程可化为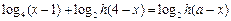 ,
,
即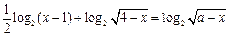 ,
,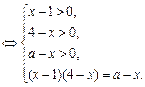
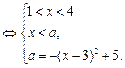
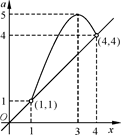
①当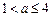 时,原方程有一解
时,原方程有一解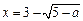 ;
;
②当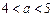 时,原方程有二解
时,原方程有二解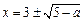 ;
;
③当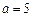 时,原方程有一解
时,原方程有一解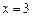 ;
;
④当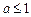 或
或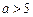 时,原方程无解.
时,原方程无解.
(Ⅲ)由已知得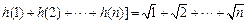 ,
,
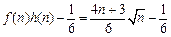 .
.
设数列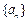 的前n项和为
的前n项和为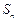 ,且
,且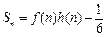 (
(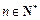 )
)
从而有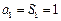 ,当
,当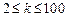 时,
时,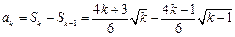 .
.
又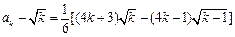
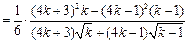
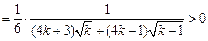 .
.
即对任意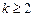 时,有
时,有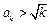 ,又因为
,又因为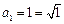 ,所以
,所以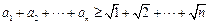 .
.
则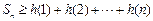 ,故原不等式成立.
,故原不等式成立.


