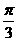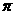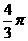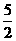(单词翻译:单击)
一,选择题:
(1)设集合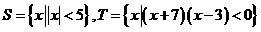 ,则
,则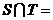
(A) {x∣-7<x<-5} (B) {x∣3<x<5 }
(C) {x∣-5<x<3} (D) {x∣-7<x<5}
(3)等差数列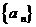 的公差不为零,首项
的公差不为零,首项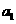 =1,
=1,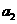 是
是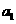 和
和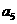 等比中项,则数列
等比中项,则数列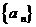 的前10项之和是
的前10项之和是
(A)90 (B) 100 (C) 145 (D) 190
(5)设矩形的长为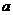 ,宽为
,宽为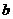 ,其比满足
,其比满足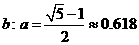 ,这种矩形给人美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本: 
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
(A)甲批次的总体平均数与标准值更接近。
(B)乙批次的总体平均数与标准值更接近
(C)两个批次总体平均数与标准值接近程度相同
(D)两个批次总体平均数与标准值接近程度不能确定
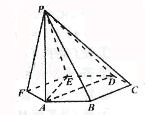
(6)如图,已知六棱锥P-ABCDEF的底面是正六边形,PA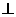 平面ABC,PA=2AB,则下列结论正确的是
平面ABC,PA=2AB,则下列结论正确的是
(C)直线BC//平面PAE 

(7)已知a,b,c,d为实数,且 ,则“a>b”是“
,则“a>b”是“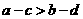 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件 

(8) 已知双曲线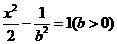 的左、右焦点分别为
的左、右焦点分别为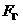
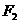 ,其一条渐进线方程为
,其一条渐进线方程为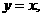 点
点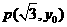 在该双曲线上,则
在该双曲线上,则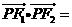
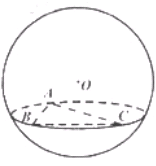
(9) 如图,在半径为3的球面上有A.B.C三点,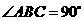 ,BA=BC,球心O到平面ABC的距离是
,BA=BC,球心O到平面ABC的距离是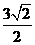 ,则B.C两点的球面距离是
,则B.C两点的球面距离是
(10) 某企业生产甲、乙两种产品。已知生产每吨甲产品要用A原料3吨、B原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨。销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是 

A 12万 B 20万 C 25万 D 27万
(11) 2位男生和3位女生共5位同学站成一排,若男生甲不站两端,3为女生中有且只有两位女生相邻,则不同排法的种数是
A 60 B 48 C 42 D 36
(12) 已知函数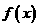 是定义在实数集R上的不恒为零的偶函数,且对任意实数x都有
是定义在实数集R上的不恒为零的偶函数,且对任意实数x都有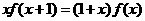 ,则
,则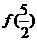 的值是
的值是
第Ⅱ卷
本卷共10小题,共90分.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13)抛物线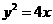 的焦点到准线的距离是________.
的焦点到准线的距离是________.
(14)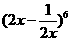 的展开式的常数项是________.(用数字作答)
的展开式的常数项是________.(用数字作答)
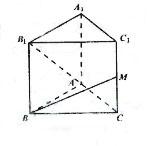
(15)如图,已知正三棱柱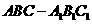 的各条棱长都相等,M是侧棱
的各条棱长都相等,M是侧棱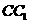 的中点,侧异面直线
的中点,侧异面直线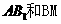 所成的角的大小是________.
所成的角的大小是________.
(16)设V是已知平面M上所有向量的集合,对于映射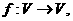
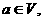 记
记
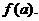 若映射
若映射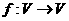 满足:对所有
满足:对所有 及任意实数
及任意实数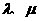 都有
都有 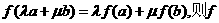 称为平面M上的线性变换,现有下列命题:
称为平面M上的线性变换,现有下列命题:
① 设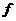 是平面M上的线性变换,
是平面M上的线性变换,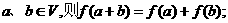
② 若e是平面M上的单位向量,对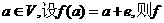 是平面M上的线性变换;
是平面M上的线性变换;
③ 对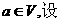
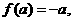 则
则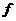 是平面M上的线性变换;
是平面M上的线性变换;
④ 设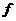 是平面M上的线性变换,
是平面M上的线性变换, ,则对任意实数k均有
,则对任意实数k均有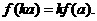
其中的真命题是 ________.(写出所有真命题的编号) 

三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
在△ABC中,A、B为锐角,角A、B、C所对的边分别为a、b、c,且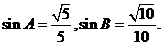
(Ⅰ)求A+B的值;
(Ⅱ)若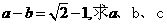 得值.
得值. 

(18)(本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡),某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中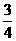 是省外游客,其余是省内游客,在省外游客中有
是省外游客,其余是省内游客,在省外游客中有 持金卡,在省内游客中有
持金卡,在省内游客中有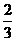 持银卡.
持银卡.
(Ⅰ)在该团中随即采访2名游客,求恰有1人持银卡的概率; 

(Ⅱ)在该团中随机采访2名游客,求其中持金卡与持银卡人数相当的概率.
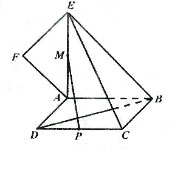
(19)(本小题满分12分)如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
(Ⅰ)求证:EF⊥平面BCE;
(Ⅱ)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE;
(Ⅲ)求二面角F-BD-A的大小.
(20)(本小题满分12分)
已知函数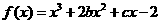 的图象在与x轴交点处的切线方程是
的图象在与x轴交点处的切线方程是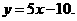
(Ⅰ)求函数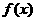 的解析式;
的解析式; 

(Ⅱ)设函数 的极值存在,求实数m的取值范围以及函数
的极值存在,求实数m的取值范围以及函数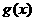 取得极值时对应的自变量x的值.
取得极值时对应的自变量x的值. 

(21)(本小题满分12分)
已知椭圆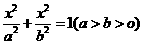 的左、右焦点分别为
的左、右焦点分别为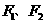 ,离心率
,离心率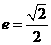 ,右准线方程为x=2.
,右准线方程为x=2. 

(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点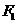 的直线
的直线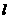 与该椭圆相交于M、N两点,且
与该椭圆相交于M、N两点,且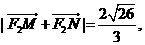 求直线
求直线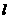 的方程式.
的方程式. 

(22)(本小题满分14分)
设数列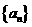 的前n项和为
的前n项和为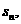 对任意的正整数n,都有
对任意的正整数n,都有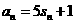 成立,记
成立,记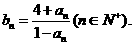


(Ⅰ)求数列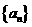 与数列
与数列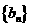 的通项公式;
的通项公式;
(Ⅱ)设数列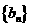 的前n项和为R
的前n项和为R ,是否存在正整数k,使得
,是否存在正整数k,使得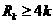 成立?若存在,找出一个正整数k;若不存在,请说明理由;
成立?若存在,找出一个正整数k;若不存在,请说明理由;
(Ⅲ)记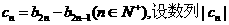 的前n项和味
的前n项和味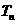 ,求证:对任意正整数n,都有
,求证:对任意正整数n,都有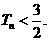
一.选择题:本题考查基本概念和基本运算。每小题5分,满分60分.
(1)C (2)C (3)B (4)D (5)A (6)D
(7) B (8)C (9)B (10)D (11)B (12)A
二.填空题:本题考查基本概念和基本运算。每小题5分,满分60分.
(13) 2 (14) -20 (15) 90 (16) 134
三.解答题
(17)本小题主要考查同角三角函数间的系统、两角和差的三角函数公式、正弦定理等基础知识及基本运算能力.
解(Ⅰ)∵A、B为锐角,sinA=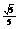 ,sinB=
,sinB=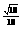 ,
,
∴cosA=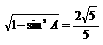 ,cosB=
,cosB=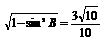


∴cos(A+B)=cosAcosB-sinAsinB=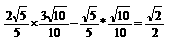
∵0<A<B<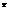 ,
,
∴A+B=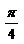 . ………………………6分
. ………………………6分
(Ⅱ)由(Ⅰ)知C=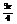 ,∴sinC=
,∴sinC=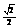 .
.
由正弦定理 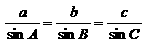 得
得
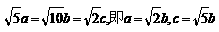
∵a-b=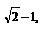
∴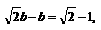
∴b=1 

∴a=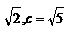 . ……………………………12分
. ……………………………12分
(18)本小题主要考查相互独立事件、互斥事件等概率计算,考查运用概率知识实际问题的能力。
解(I)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡。
设事件A为“采访该团2人,恰有1人持银卡。
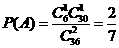
所以采访该团2人,恰有1人持银行卡的概率是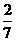
(Ⅱ)设事件B为“采访该团2人中,持金卡人数与持银卡人数相等”,
事件 为“采访该团2人中,0人持金卡,0人持银卡”,
为“采访该团2人中,0人持金卡,0人持银卡”,
事件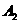 为“采访该团2人中,1人持金卡,1人持银卡”,
为“采访该团2人中,1人持金卡,1人持银卡”,
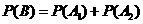

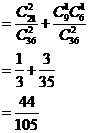
所以采访该团2人中,持金卡人数与持银卡人数相等的概率是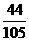 ………………………..12分
………………………..12分
(19题)本小题主要考查平面与平面垂直、直线与平面垂直、直线与平面平行、二面角等基础知识,考查空间想象能力、逻辑推理能力,考查应用向量知识解决数学问题的能力。
解法一:
(Ⅰ)因为平面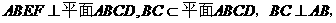
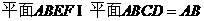
所以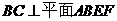
因为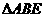 为等腰直角三角形,
为等腰直角三角形,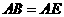 ,
,
所以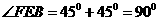
即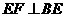
因为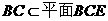 ,
,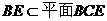
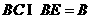 ,
,
所以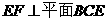
(Ⅱ)取BE的中点N,连结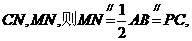
所以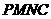 为平行四边形,所以
为平行四边形,所以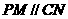
因为 在平面
在平面 内,
内,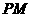 不在平面
不在平面 内,
内,
所以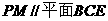
(Ⅲ)由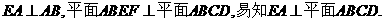
作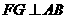 交
交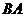 的延长线与
的延长线与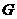 则,
则,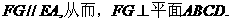
作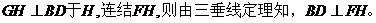
因此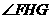 为二面角
为二面角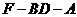 的平面角
的平面角
因此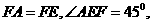
所以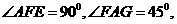
设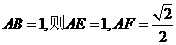
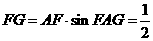
在Rt△BGH中∠GBH=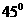 ,BG=AB+AG=1+
,BG=AB+AG=1+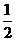 =
=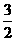 。
。
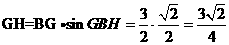
在Rt△FGH中,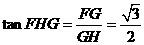
故二面角F-BD-A的大小为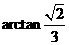 ………………….12分
………………….12分
解法二:
(Ⅰ)因为△ABE为等腰直角三角形,AB=AE,
所以AE⊥AB,
又因为平面ABEF⊥平面ABCD,AE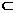 平面ABEF
平面ABEF
平面ABEF  平面ABCD= AB
平面ABCD= AB
所以AE⊥平面ABCD
所以AE⊥AD
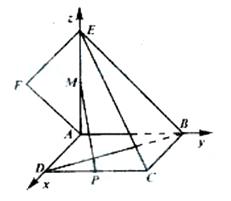
因此,AD,AB,AE两两垂直,建立如图所示的直角坐
标系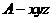 .
.
设AB=1,则AE=1,B(0,1,0),D(1,0,0),
E(0,0,1),C(1,1,0)
因为FA=FE,∠AEF=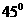 ,
,
所以∠AEF=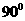 .
.
从而,F(0,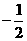 ,
,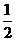 ).
).
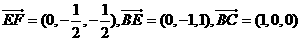 .
.
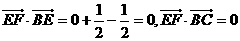
所以EF⊥BE,EF⊥BC.
因为BE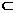 平面BCE,BC
平面BCE,BC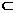 平面BCE,BC
平面BCE,BC BE=B,
BE=B,
所以EF⊥平面BCE. …………………………………4分
(Ⅱ)M(0,0,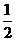 ).P(1,
).P(1, 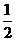 ,0).
,0).
从而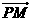 =(
=(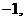
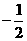 ,
,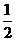 ).
).
于是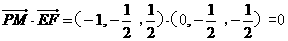
所以PM⊥FE,又EF⊥平面BCE,直线PM不在平面BCE内,
故PM∥平面BCE. ………………………8分
(Ⅲ)设平面BDF的一个法向量为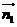 ,并设
,并设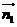 =(x,y,z)
=(x,y,z)
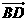 =(1,
=(1,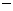 1,0),
1,0),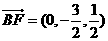
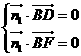 即
即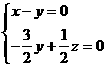
去y=1,则x=1,z=3,从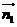 =(0,0,3)
=(0,0,3)
取平面ABD的一个法向量为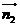 =(0,0,1)
=(0,0,1)
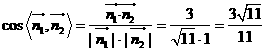
故二面角F-BD-A的大小为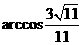 . ……………………….12分
. ……………………….12分
(20)本小题考查函数、函数极值的概念,考查应用导数研究函数性质的方法及推理和运算能力。
解:(Ⅰ)由已知,切点为(2,0)故有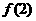 =0,即4b+c+3=0 …….①
=0,即4b+c+3=0 …….①
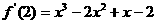 ,由已知
,由已知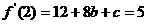 .
.
得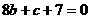 …..② 联立①、②,解得c=1,b=
…..② 联立①、②,解得c=1,b=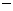 1
1
于是函数解析式为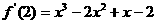 ……………..4分
……………..4分
(Ⅱ)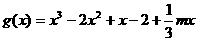
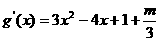 ,令
,令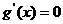
当函数有极值时,△ 0,方程
0,方程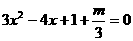 有实根,
有实根,
由△=4(1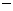 m)
m) 0,得m
0,得m  1
1
①当m=1时,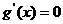 有实根
有实根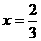 ,在
,在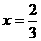 左右两侧均有
左右两侧均有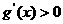 ,故
,故
函数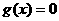 无极值。
无极值。
②m  1时,
1时,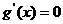 有两个实根,
有两个实根,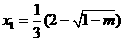 ,
,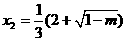 ,
,
当x变化时,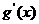 、
、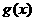 的变化情况如下表:
的变化情况如下表:
故在m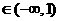 时,函数
时,函数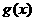 有极值:
有极值:
当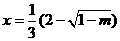 时
时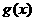 有极大值;
有极大值;
当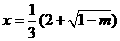 时
时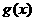 有极大值。………………………12分
有极大值。………………………12分
(21)本小题主要考查直线、椭圆、平面向量等基础知识,以及综合运用数学知识解决问题及推理运算能力。
解:(Ⅰ)由条件有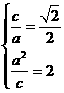 解得a=
解得a=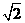 ,c=1
,c=1 

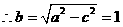
所以,所求椭圆的方程为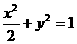 ………………….4分
………………….4分
(Ⅱ)由(Ⅰ)知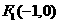 、
、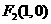


若直线L的斜率不存在,则直线L的方程为x= —1,
将x= —1代入椭圆方程的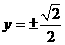
不妨设M 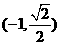 、N
、N 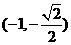
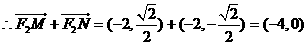
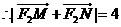 ,与题设矛盾。
,与题设矛盾。 

∴直线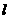 的斜率存在
的斜率存在
设直线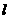 的斜率为
的斜率为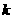 ,则直线
,则直线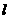 的方程为
的方程为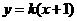
设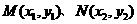
联立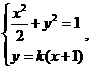 消
消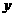 得
得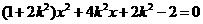
由根与系数的关系知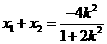 ,从而
,从而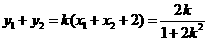
又∵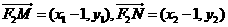 ,
, 

∴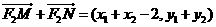
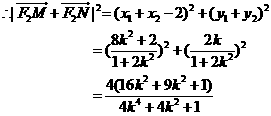
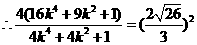


化简得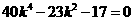
解得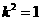 或
或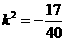 (舍)
(舍)
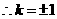
∴所求直线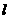 的方程为
的方程为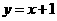 或
或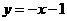
(22)本小题主要考查数列、不等式等基础知识,化归思想等数学思想方法,以及推理论证、分析与解决问题的能力。
解:(Ⅰ)当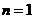 时,
时,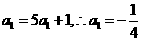
又∵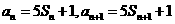
∴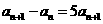 ,即
,即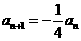
∴数列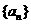 成等比数列,其首项
成等比数列,其首项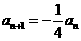


∴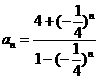
(Ⅱ)不存在正整数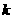 ,使得
,使得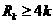 成立
成立
下证:对任意的正整数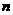 ,都有
,都有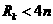 成立
成立 

由(Ⅰ)知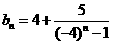
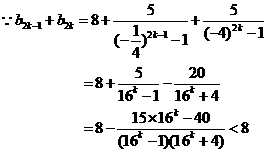



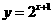
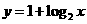
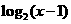
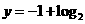
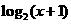
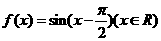
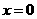 对称
对称