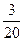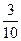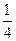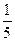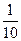(单词翻译:单击)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合M={-1,0,1},N={x|x2≤x},则M∩N=
A.{0} B.{0,1} C.{-1,1} D.{-1,0,0}
【答案】B
【解析】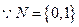 M={-1,0,1}
M={-1,0,1}  M∩N={0,1}.
M∩N={0,1}.
【点评】本题考查了集合的基本运算,较简单,易得分.
先求出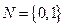 ,再利用交集定义得出M∩N.
,再利用交集定义得出M∩N.
【答案】C
【解析】因为“若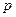 ,则
,则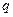 ”的逆否命题为“若
”的逆否命题为“若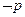 ,则
,则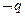 ”,所以 “若α=
”,所以 “若α=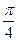 ,则tanα=1”的逆否命题是 “若tanα≠1,则α≠
,则tanα=1”的逆否命题是 “若tanα≠1,则α≠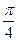 ”.
”.
【点评】本题考查了“若p,则q”形式的命题的逆命题、否命题与逆否命题,考查分析问题的能力.
3.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是
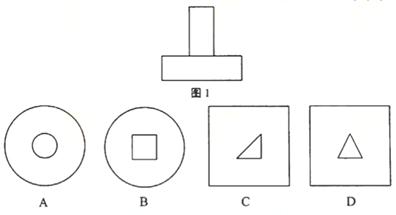
【答案】D
【解析】本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.
【点评】本题主要考查空间几何体的三视图,考查空间想象能力.是近年高考中的热点题型.
4.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为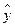 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A.y与x具有正的线性相关关系
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重比为58.79kg
【答案】D
【解析】【解析】由回归方程为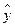 =0.85x-85.71知
=0.85x-85.71知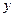 随
随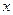 的增大而增大,所以y与x具有正的线性相关关系,由最小二乘法建立的回归方程得过程知
的增大而增大,所以y与x具有正的线性相关关系,由最小二乘法建立的回归方程得过程知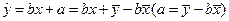 ,所以回归直线过样本点的中心(
,所以回归直线过样本点的中心(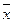 ,
,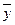 ),利用回归方程可以预测估计总体,所以D不正确.
),利用回归方程可以预测估计总体,所以D不正确.
【点评】本题组要考查两个变量间的相关性、最小二乘法及正相关、负相关的概念,并且是找不正确的答案,易错.
5. 已知双曲线C :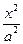 -
-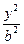 =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
又 C 的渐近线为
C 的渐近线为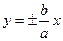 ,点P (2,1)在C 的渐近线上,
,点P (2,1)在C 的渐近线上,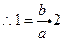 ,即
,即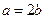 .
.
【点评】本题考查双曲线的方程、双曲线的渐近线方程等基础知识,考查了数形结合的思想和基本运算能力,是近年来常考题型.
A. [ -2 ,2] B.[-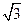 ,
,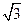 ] C.[-1,1 ] D.[-
] C.[-1,1 ] D.[-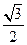 ,
, 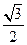 ]
]
【答案】B
【解析】f(x)=sinx-cos(x+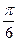 )
)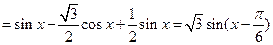 ,
,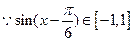 ,
,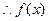 值域为[-
值域为[-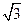 ,
,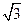 ].
].
【点评】利用三角恒等变换把 化成
化成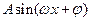 的形式,利用
的形式,利用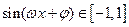 ,求得
,求得 的值域.
的值域.
7. 在△ABC中,AB=2,AC=3,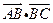 = 1则
= 1则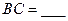 .
.
【答案】A
【解析】由下图知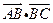

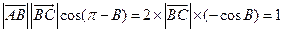 .
.
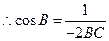 .又由余弦定理知
.又由余弦定理知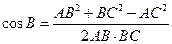 ,解得
,解得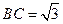 .
.
【点评】本题考查平面向量的数量积运算、余弦定理等知识.考查运算能力,考查数形结合思想、等价转化思想等数学思想方法.需要注意 的夹角为
的夹角为 的外角.
的外角.
8.已知两条直线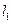 :y=m 和
:y=m 和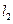 : y=
: y=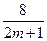 (m>0),
(m>0),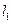 与函数
与函数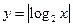 的图像从左至右相交于点A,B ,
的图像从左至右相交于点A,B ,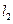 与函数
与函数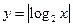 的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a ,b ,当m 变化时,
的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a ,b ,当m 变化时,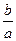 的最小值为
的最小值为
【答案】B
【解析】在同一坐标系中作出y=m,y=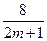 (m>0),
(m>0),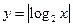 图像如下图,
图像如下图,
依照题意得
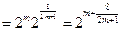 .
.
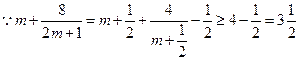 ,
,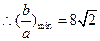 .
.
【点评】在同一坐标系中作出y=m,y=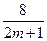 (m>0),
(m>0),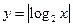 图像,结合图像可解得.
图像,结合图像可解得.
二 、填空题: 本大题共8小题,考生作答7小题,每小题5分 ,共35分,把答案填在答题卡中对应题号后的横线上.
(一)选做题(请考生在第9、10、 11三题中任选两题作答,如果全做,则按前两题记分 )
9. 在直角坐标系xOy 中,已知曲线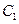 :
: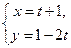 (t为参数)与曲线
(t为参数)与曲线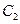 :
: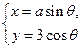
【答案】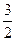
【解析】曲线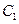 :
: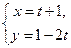 直角坐标方程为
直角坐标方程为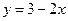 ,与
,与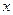 轴交点为
轴交点为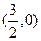 ;
;
曲线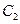 :
: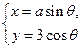 直角坐标方程为
直角坐标方程为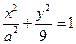 ,其与
,其与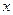 轴交点为
轴交点为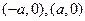 ,
,
由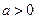 ,曲线
,曲线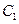 与曲线
与曲线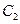 有一个公共点在X轴上,知
有一个公共点在X轴上,知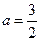 .
.
【点评】本题考查直线的参数方程、椭圆的参数方程,考查等价转化的思想方法等.曲线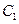 与曲线
与曲线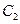 的参数方程分别等价转化为直角坐标方程,找出与
的参数方程分别等价转化为直角坐标方程,找出与 轴交点,即可求得.
轴交点,即可求得.
10.不等式|2x+1|-2|x-1|>0的解集为_______.
【答案】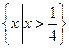
【解析】令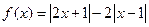 ,则由
,则由
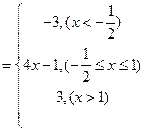 得
得
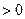 的解集为
的解集为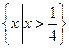 .
.
【点评】绝对值不等式解法的关键步骤是去绝对值,转化为代数不等式(组).
11.如图2,过点P的直线与圆O相交于A,B两点.若PA=1,AB=2,PO=3,则圆O的半径等于_______.
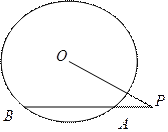
【答案】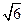
【解析】设 交圆O于C,D,如图,设圆的半径为R,由割线定理知
交圆O于C,D,如图,设圆的半径为R,由割线定理知
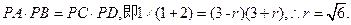
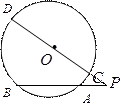
【点评】本题考查切割线定理,考查数形结合思想,由切割线定理知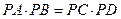 ,从而求得圆的半径.
,从而求得圆的半径.
(二)必做题(12~16题)
12.已知复数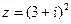 (i为虚数单位),则|z|=_____.
(i为虚数单位),则|z|=_____.
【答案】10
【解析】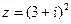 =
=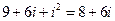 ,
,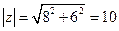 .
.
【点评】本题考查复数的运算、复数的模.把复数化成标准的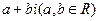 形式,利用
形式,利用
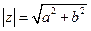 求得.
求得.
【答案】-160
【解析】(  -
-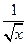 )6的展开式项公式是
)6的展开式项公式是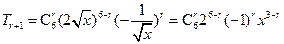 .由题意知
.由题意知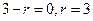 ,所以二项展开式中的常数项为
,所以二项展开式中的常数项为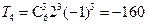 .
.
【点评】本题主要考察二项式定理,写出二项展开式的通项公式是解决这类问题的常规办法.
14.如果执行如图3所示的程序框图,输入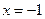 ,n=3,则输出的数S= .
,n=3,则输出的数S= .
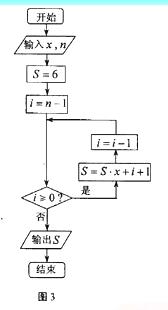
【答案】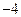
【解析】输入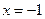 ,n=3,,执行过程如下:
,n=3,,执行过程如下: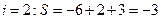 ;
;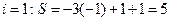 ;
;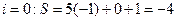 ,所以输出的是
,所以输出的是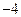 .
.
【点评】本题考查算法流程图,要明白循环结构中的内容,一般解法是逐步执行,一步步将执行结果写出,特别是程序框图的执行次数不能出错.
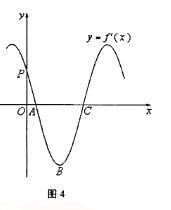
15.函数f(x)=sin (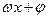 )的导函数
)的导函数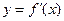 的部分图像如图4所示,其中,P为图像与y轴的交点,A,C为图像与x轴的两个交点,B为图像的最低点.
的部分图像如图4所示,其中,P为图像与y轴的交点,A,C为图像与x轴的两个交点,B为图像的最低点.
(2)若在曲线段 与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 .
与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 .
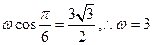 ;
;
(2)由图知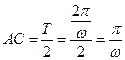 ,
,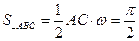 ,设
,设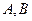 的横坐标分别为
的横坐标分别为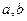 .
.
设曲线段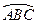 与x轴所围成的区域的面积为
与x轴所围成的区域的面积为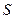 则
则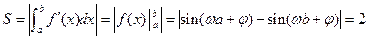 ,由几何概型知该点在△ABC内的概率为
,由几何概型知该点在△ABC内的概率为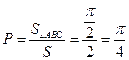 .
.
【点评】本题考查三角函数的图像与性质、几何概型等,(1)利用点P在图像上求 ,
,
(2)几何概型,求出三角形面积及曲边形面积,代入公式即得.
16.设N=2n(n∈N*,n≥2),将N个数x1,x2,…,xN依次放入编号为1,2,…,N的N个位置,得到排列P0=x1x2…xN.将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前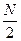 和后
和后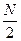 个位置,得到排列P1=x1x3…xN-1x2x4…xN,将此操作称为C变换,将P1分成两段,每段
个位置,得到排列P1=x1x3…xN-1x2x4…xN,将此操作称为C变换,将P1分成两段,每段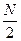 个数,并对每段作C变换,得到
个数,并对每段作C变换,得到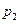 ;当2≤i≤n-2时,将Pi分成2i段,每段
;当2≤i≤n-2时,将Pi分成2i段,每段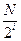 个数,并对每段C变换,得到Pi+1,例如,当N=8时,P2=x1x5x3x7x2x6x4x8,此时x7位于P2中的第4个位置.
个数,并对每段C变换,得到Pi+1,例如,当N=8时,P2=x1x5x3x7x2x6x4x8,此时x7位于P2中的第4个位置.
(1)当N=16时,x7位于P2中的第___个位置;
(2)当N=2n(n≥8)时,x173位于P4中的第___个位置.
【答案】(1)6;(2)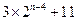
【解析】(1)当N=16时,
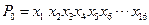 ,可设为
,可设为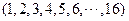 ,
,
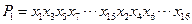 ,即为
,即为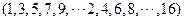 ,
,
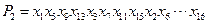 ,即
,即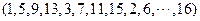 , x7位于P2中的第6个位置,;
, x7位于P2中的第6个位置,;
(2)方法同(1),归纳推理知x173位于P4中的第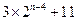 个位置.
个位置.
【点评】本题考查在新环境下的创新意识,考查运算能力,考查创造性解决问题的能力.
需要在学习中培养自己动脑的习惯,才可顺利解决此类问题.
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数(人) |
| 30 | 25 |
| 10 |
结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.
(注:将频率视为概率)
【解析】(1)由已知,得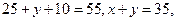 所以
所以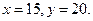
该超市所有顾客一次购物的结算时间组成一个总体,所以收集的100位顾客一次购物的结算时间可视为总体的一个容量随机样本,将频率视为概率得
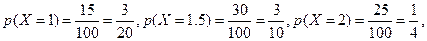
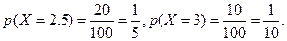
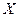 的分布为
的分布为
X | 1 | 1.5 | 2 | 2.5 | 3 |
P |
|
|
|
|
|
X的数学期望为
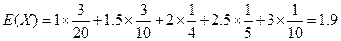 .
.
(Ⅱ)记A为事件“该顾客结算前的等候时间不超过2.5分钟”,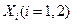 为该顾客前面第
为该顾客前面第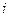 位顾客的结算时间,则
位顾客的结算时间,则
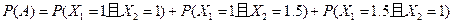 .
.
由于顾客的结算相互独立,且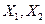 的分布列都与X的分布列相同,所以
的分布列都与X的分布列相同,所以
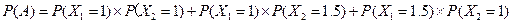
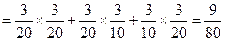 .
.
故该顾客结算前的等候时间不超过2.5分钟的概率为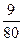 .
.
【点评】本题考查概率统计的基础知识,考查分布列及数学期望的计算,考查运算能力、分析问题能力.第一问中根据统计表和100位顾客中的一次购物量超过8件的顾客占55%知
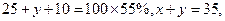 从而解得
从而解得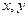 ,计算每一个变量对应的概率,从而求得分布列和期望;第二问,通过设事件,判断事件之间互斥关系,从而求得该顾客结算前的等候时间不超过2.5分钟的概率.
,计算每一个变量对应的概率,从而求得分布列和期望;第二问,通过设事件,判断事件之间互斥关系,从而求得该顾客结算前的等候时间不超过2.5分钟的概率.
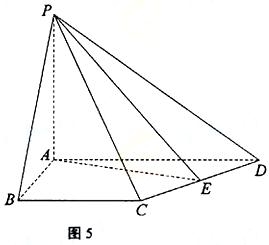
18.(本小题满分12分)
如图5,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
(Ⅰ)证明:CD⊥平面PAE;
(Ⅱ)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
【解析】
解法1(Ⅰ如图(1)),连接AC,由AB=4,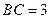 ,
,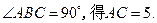
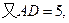 E是CD的中点,所以
E是CD的中点,所以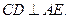
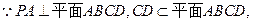 所以
所以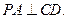
而 内的两条相交直线,所以CD⊥平面PAE.
内的两条相交直线,所以CD⊥平面PAE.
(Ⅱ)过点B作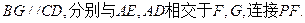
由(Ⅰ)CD⊥平面PAE知,BG⊥平面PAE.于是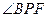 为直线PB与平面PAE
为直线PB与平面PAE
所成的角,且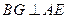 .
.
由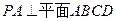 知,
知,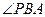 为直线
为直线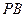 与平面
与平面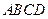 所成的角.
所成的角.
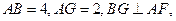 由题意,知
由题意,知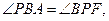
因为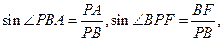 所以
所以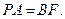
由 所以四边形
所以四边形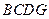 是平行四边形,故
是平行四边形,故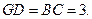 于是
于是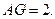
在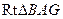 中,
中,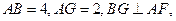 所以
所以
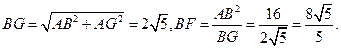
于是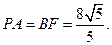
又梯形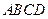 的面积为
的面积为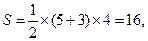 所以四棱锥
所以四棱锥 的体积为
的体积为
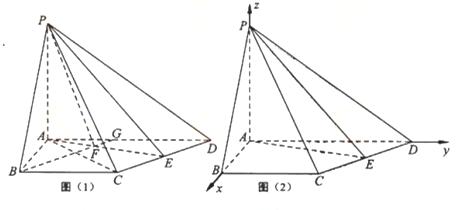
解法2:如图(2),以A为坐标原点, 所在直线分别为
所在直线分别为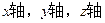 建立空间直角坐标系.设
建立空间直角坐标系.设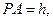 则相关的各点坐标为:
则相关的各点坐标为:
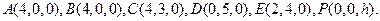
(Ⅰ)易知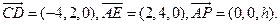 因为
因为
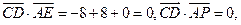 所以
所以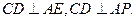 而
而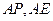 是平面
是平面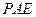 内的两条相交直线,所以
内的两条相交直线,所以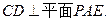
(Ⅱ)由题设和(Ⅰ)知,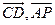 分别是
分别是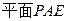 ,
,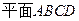 的法向量,而PB与
的法向量,而PB与
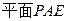 所成的角和PB与
所成的角和PB与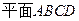 所成的角相等,所以
所成的角相等,所以
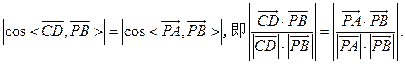
由(Ⅰ)知,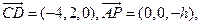 由
由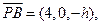 故
故
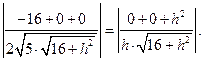
解得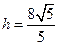 .
.
又梯形ABCD的面积为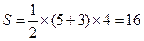 ,所以四棱锥
,所以四棱锥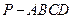 的体积为
的体积为
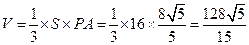 .
.
【点评】本题考查空间线面垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明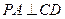 即可,第二问算出梯形的面积和棱锥的高,由
即可,第二问算出梯形的面积和棱锥的高,由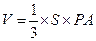 算得体积,或者建立空间直角坐标系,求得高几体积.
算得体积,或者建立空间直角坐标系,求得高几体积.
19.(本小题满分12分)
已知数列{an}的各项均为正数,记A(n)=a1+a2+……+an,B(n)=a2+a3+……+an+1,C(n)=a3+a4+……+an+2,n=1,2,……
(1) 若a1=1,a2=5,且对任意n∈N﹡,三个数A(n),B(n),C(n)组成等差数列,求数列{ an }的通项公式.
(2) 证明:数列{ an }是公比为q的等比数列的充分必要条件是:对任意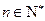 ,三个数A(n),B(n),C(n)组成公比为q的等比数列.
,三个数A(n),B(n),C(n)组成公比为q的等比数列.
【解析】
解(1)对任意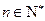 ,三个数
,三个数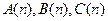 是等差数列,所以
是等差数列,所以
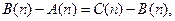
即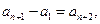 亦即
亦即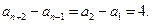
故数列 是首项为1,公差为4的等差数列.于是
是首项为1,公差为4的等差数列.于是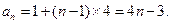
(Ⅱ)(1)必要性:若数列 是公比为q的等比数列,则对任意
是公比为q的等比数列,则对任意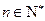 ,有
,有
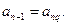 由
由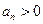 知,
知,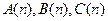 均大于0,于是
均大于0,于是
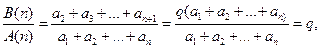
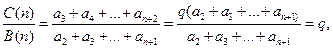
即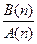 =
=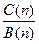 =
=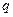 ,所以三个数
,所以三个数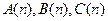 组成公比为
组成公比为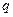 的等比数列.
的等比数列.
(2)充分性:若对于任意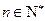 ,三个数
,三个数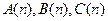 组成公比为
组成公比为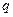 的等比数列,
的等比数列,
则
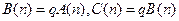 ,
,
于是 得
得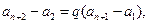 即
即
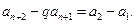
由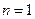 有
有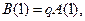 即
即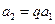 ,从而
,从而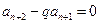 .
.
因为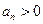 ,所以
,所以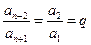 ,故数列
,故数列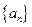 是首项为
是首项为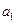 ,公比为
,公比为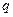 的等比数列,
的等比数列,
综上所述,数列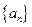 是公比为
是公比为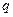 的等比数列的充分必要条件是:对任意n∈N﹡,三个数
的等比数列的充分必要条件是:对任意n∈N﹡,三个数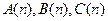 组成公比为
组成公比为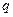 的等比数列.
的等比数列.
【点评】本题考查等差数列、等比数列的定义、性质及充要条件的证明.第一问由等差数列定义可得;第二问要从充分性、必要性两方面来证明,利用等比数列的定义及性质易得证.
20.(本小题满分13分)
某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
【解析】
解:(Ⅰ)设完成A,B,C三种部件的生产任务需要的时间(单位:天)分别为
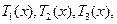 由题设有
由题设有
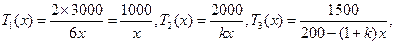
期中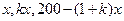 均为1到200之间的正整数.
均为1到200之间的正整数.
(Ⅱ)完成订单任务的时间为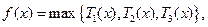 其定义域为
其定义域为
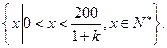 易知,
易知,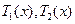 为减函数,
为减函数,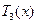 为增函数.注意到
为增函数.注意到
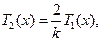 于是
于是
(1)当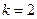 时,
时,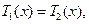 此时
此时
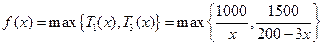 ,
,
由函数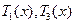 的单调性知,当
的单调性知,当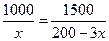 时
时 取得最小值,解得
取得最小值,解得
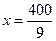 .由于
.由于
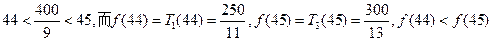 .
.
故当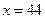 时完成订单任务的时间最短,且最短时间为
时完成订单任务的时间最短,且最短时间为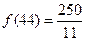 .
.
(2)当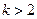 时,
时,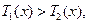 由于
由于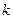 为正整数,故
为正整数,故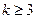 ,此时
,此时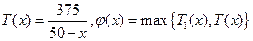 易知
易知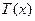 为增函数,则
为增函数,则
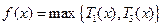
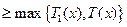
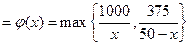 .
.
由函数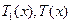 的单调性知,当
的单调性知,当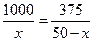 时
时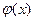 取得最小值,解得
取得最小值,解得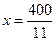 .由于
.由于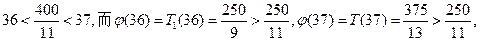
此时完成订单任务的最短时间大于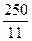 .
.
(3)当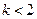 时,
时,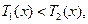 由于
由于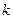 为正整数,故
为正整数,故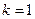 ,此时
,此时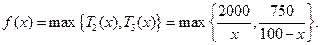 由函数
由函数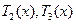 的单调性知,
的单调性知,
当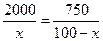 时
时 取得最小值,解得
取得最小值,解得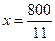 .类似(1)的讨论.此时
.类似(1)的讨论.此时
完成订单任务的最短时间为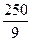 ,大于
,大于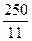 .
.
综上所述,当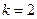 时完成订单任务的时间最短,此时生产A,B,C三种部件的人数
时完成订单任务的时间最短,此时生产A,B,C三种部件的人数
分别为44,88,68.
【点评】本题为函数的应用题,考查分段函数、函数单调性、最值等,考查运算能力及用数学知识分析解决实际应用问题的能力.第一问建立函数模型;第二问利用单调性与最值来解决,体现分类讨论思想.
21.(本小题满分13分)
在直角坐标系xOy中,曲线C1的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(Ⅰ)求曲线C1的方程;
(Ⅱ)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
【解析】(Ⅰ)解法1 :设M的坐标为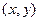 ,由已知得
,由已知得
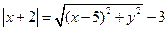 ,
,
易知圆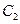 上的点位于直线
上的点位于直线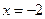 的右侧.于是
的右侧.于是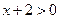 ,所以
,所以
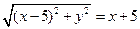 .
.
化简得曲线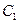 的方程为
的方程为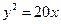 .
.
解法2 :由题设知,曲线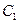 上任意一点M到圆心
上任意一点M到圆心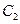
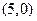 的距离等于它到直线
的距离等于它到直线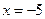 的距离,因此,曲线
的距离,因此,曲线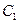 是以
是以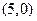 为焦点,直线
为焦点,直线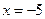 为准线的抛物线,故其方程为
为准线的抛物线,故其方程为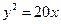 .
.
(Ⅱ)当点P在直线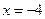 上运动时,P的坐标为
上运动时,P的坐标为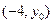 ,又
,又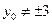 ,则过P且与圆
,则过P且与圆
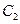 相切得直线的斜率
相切得直线的斜率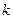 存在且不为0,每条切线都与抛物线有两个交点,切线方程为
存在且不为0,每条切线都与抛物线有两个交点,切线方程为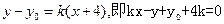 .于是
.于是
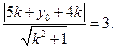
整理得
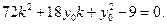 ①
①
设过P所作的两条切线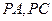 的斜率分别为
的斜率分别为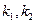 ,则
,则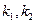 是方程①的两个实根,故
是方程①的两个实根,故
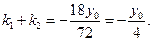 ②
②
由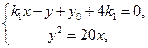 得
得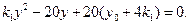 ③
③
设四点A,B,C,D的纵坐标分别为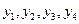 ,则是方程③的两个实根,所以
,则是方程③的两个实根,所以
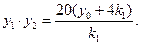 ④
④
同理可得
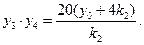 ⑤
⑤
于是由②,④,⑤三式得
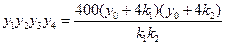
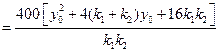
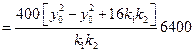 .
.
所以,当P在直线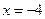 上运动时,四点A,B,C,D的纵坐标之积为定值6400.
上运动时,四点A,B,C,D的纵坐标之积为定值6400.
【点评】本题考查曲线与方程、直线与曲线的位置关系,考查运算能力,考查数形结合思想、函数与方程思想等数学思想方法.第一问用直接法或定义法求出曲线的方程;第二问设出切线方程,把直线与曲线方程联立,由一元二次方程根与系数的关系得到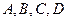 四点纵坐标之积为定值,体现“设而不求”思想.
四点纵坐标之积为定值,体现“设而不求”思想.
22.(本小题满分13分)
已知函数 =
=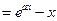 ,其中a≠0.
,其中a≠0.
(1) 若对一切x∈R, ≥1恒成立,求a的取值集合.
≥1恒成立,求a的取值集合.
(2)在函数 的图像上取定两点
的图像上取定两点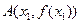 ,
,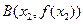
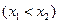 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使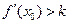 成立?若存在,求
成立?若存在,求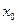 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【解析】(Ⅰ)若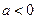 ,则对一切
,则对一切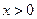 ,
,
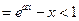 ,这与题设矛盾,又
,这与题设矛盾,又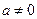 ,
,
故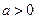 .
.
而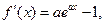 令
令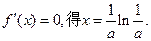
当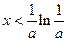 时,
时,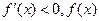 单调递减;当
单调递减;当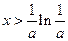 时,
时,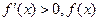 单调递增,故当
单调递增,故当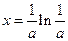 时,
时, 取最小值
取最小值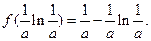
于是对一切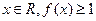 恒成立,当且仅当
恒成立,当且仅当
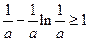 . ①
. ①
令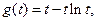 则
则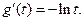
当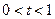 时,
时,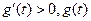 单调递增;当
单调递增;当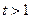 时,
时,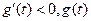 单调递减.
单调递减.
故当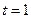 时,
时,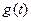 取最大值
取最大值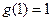 .因此,当且仅当
.因此,当且仅当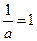 即
即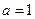 时,①式成立.
时,①式成立.
综上所述,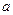 的取值集合为
的取值集合为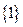 .
.
(Ⅱ)由题意知,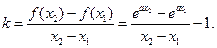
令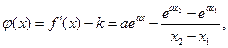 则
则
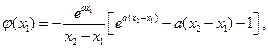
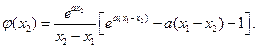
令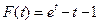 ,则
,则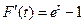 .
.
当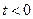 时,
时,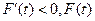 单调递减;当
单调递减;当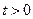 时,
时,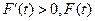 单调递增.
单调递增.
故当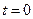 ,
,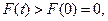 即
即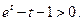
从而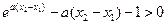 ,
,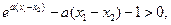 又
又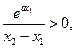
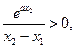
所以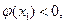
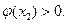
因为函数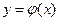 在区间
在区间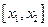 上的图像是连续不断的一条曲线,所以存在
上的图像是连续不断的一条曲线,所以存在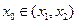 使
使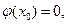
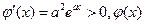 单调递增,故这样的
单调递增,故这样的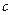 是唯一的,且
是唯一的,且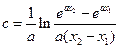 .故当且仅当
.故当且仅当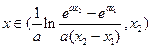 时,
时, 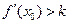 .
.
综上所述,存在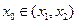 使
使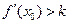 成立.且
成立.且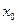 的取值范围为
的取值范围为
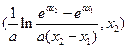 .
.
【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等,考查运算能力,考查分类讨论思想、函数与方程思想,转化与划归思想等数学思想方法.第一问利用导函数法求出 取最小值
取最小值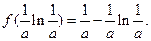 对一切x∈R,f(x)
对一切x∈R,f(x) 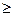 1恒成立转化为
1恒成立转化为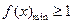 ,从而得出a的取值集合;第二问在假设存在的情况下进行推理,通过构造函数,研究这个函数的单调性及最值来进行分析判断.
,从而得出a的取值集合;第二问在假设存在的情况下进行推理,通过构造函数,研究这个函数的单调性及最值来进行分析判断.

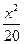
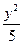
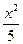
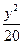
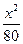
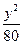
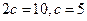 .
.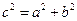 ,
,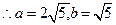 ,
,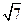
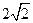
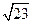
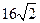
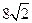
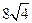
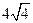
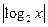 = m,得
= m,得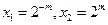 ,
,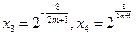 .
.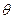
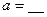 .
.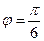 ,点P的坐标为(0,
,点P的坐标为(0,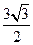
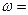 ;
;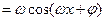 ,当
,当