(单词翻译:单击)
第Ⅰ卷
一.选择题:共12小题,每小题5分,共60分。在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
1.已知集合A={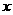 |
|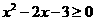 },B=
},B=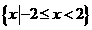 ,则
,则 =
=
 .[-2,-1]
.[-2,-1] 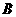 .[-1,2)
.[-1,2) 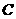 .[-1,1]
.[-1,1] 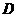 .[1,2)
.[1,2)
【答案】:A
【解析】:∵A={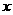 |
|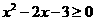 }=
}=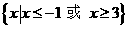 ,B=
,B=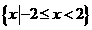 ,
,
∴ =
=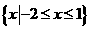 ,选A..
,选A..
2.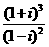 =
=
 .
.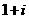
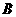 .
.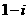
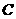 .
.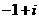
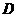 .
.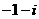
【答案】:D
【解析】:∵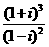 =
=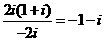 ,选D..
,选D..
3.设函数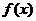 ,
,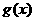 的定义域都为R,且
的定义域都为R,且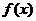 是奇函数,
是奇函数,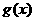 是偶函数,则下列结论正确的是
是偶函数,则下列结论正确的是
 .
.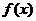
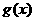 是偶函数
是偶函数 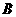 .|
.|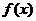 |
|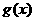 是奇函数
是奇函数
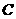 .
.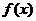 |
|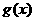 |是奇函数
|是奇函数 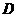 .|
.|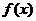
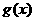 |是奇函数
|是奇函数
【答案】:C
【解析】:设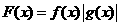 ,则
,则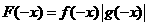 ,∵
,∵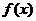 是奇函数,
是奇函数,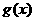 是偶函数,∴
是偶函数,∴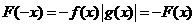 ,
,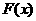 为奇函数,选C.
为奇函数,选C.
4.已知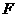 是双曲线
是双曲线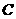 :
: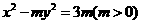 的一个焦点,则点
的一个焦点,则点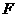 到
到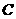 的一条渐近线的距离为
的一条渐近线的距离为
 .
.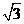
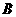 .3
.3 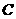 .
.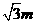
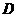 .
.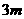
【答案】:A
【解析】:由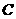 :
: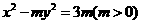 ,得
,得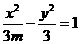 ,
,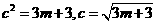
设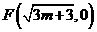 ,一条渐近线
,一条渐近线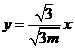 ,即
,即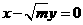 ,则点
,则点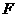 到
到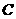 的一条渐近线的距离
的一条渐近线的距离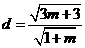 =
=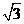 ,选A. .
,选A. .
5.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率
 .
.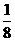
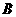 .
.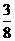
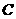 .
.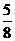
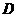 .
.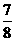
【答案】:D
【解析】:4位同学各自在周六、周日两天中任选一天参加公益活动共有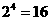 种,
种,
周六、周日都有同学参加公益活动有两种情况:①一天一人一天三人有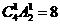 种;②每天2人有
种;②每天2人有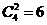 种,则周六、周日都有同学参加公益活动的概率为
种,则周六、周日都有同学参加公益活动的概率为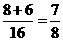 ;或间接解法:4位同学都在周六或周日参加公益活动有2种,则周六、周日都有同学参加公益活动的概率为
;或间接解法:4位同学都在周六或周日参加公益活动有2种,则周六、周日都有同学参加公益活动的概率为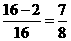 ;选D.
;选D.
6.如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角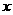 的始边为射线
的始边为射线 ,终边为射线
,终边为射线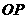 ,过点
,过点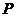 作直线
作直线 的垂线,垂足为
的垂线,垂足为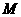 ,将点
,将点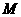 到直线
到直线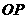 的距离表示为
的距离表示为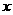 的函数
的函数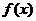 ,则
,则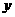 =
=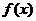 在[0,
在[0,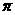 ]上的图像大致为
]上的图像大致为
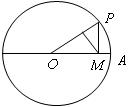

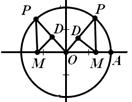 【答案】:B
【答案】:B
【解析】:如图:过M作MD⊥OP于D,则 PM= ,OM=
,OM= ,在
,在 中,MD=
中,MD=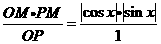

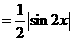 ,∴
,∴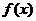
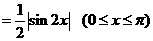 ,选B. .
,选B. .
7.执行下图的程序框图,若输入的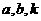 分别为1,2,3,则输出的
分别为1,2,3,则输出的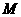 =
=

 .
.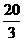
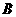 .
.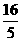
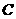 .
.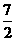
 .
.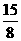
【答案】:D
【解析】:输入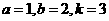 ;
;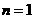 时:
时: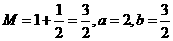 ;
;
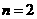 时:
时: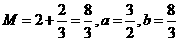 ;
;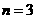 时:
时: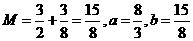 ;
;
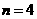 时:输出
时:输出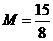 . 选D.
. 选D.
8.设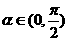 ,
,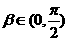 ,且
,且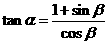 ,则
,则
 .
.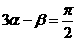
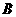 .
.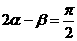
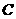 .
.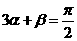
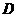 .
.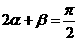
【答案】:B
【解析】:∵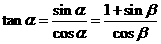 ,∴
,∴
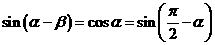 ,
,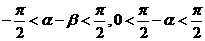
∴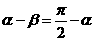 ,即
,即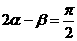 ,选B
,选B
9.不等式组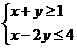 的解集记为
的解集记为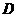 .有下面四个命题:
.有下面四个命题:
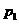 :
: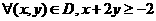 ,
,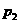 :
: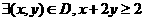 ,
,
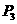 :
: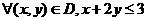 ,
,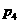 :
: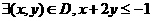 .
.
其中真命题是
 .
.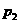 ,
,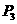
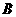 .
.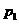 ,
,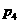
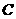 .
.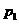 ,
,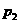
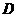 .
.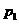 ,
,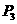
 【答案】:C
【答案】:C
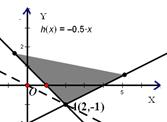
【解析】:作出可行域如图:设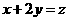 ,即
,即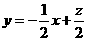 ,当直线过
,当直线过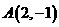 时,
时,
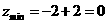 ,∴
,∴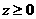 ,∴命题
,∴命题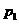 、
、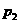 真命题,选C.
真命题,选C.
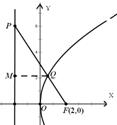
10.已知抛物线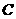 :
: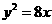 的焦点为
的焦点为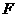 ,准线为
,准线为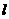 ,
,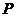 是
是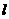 上一点,
上一点,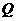 是直线
是直线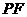 与
与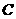 的一个交点,若
的一个交点,若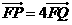 ,则
,则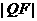 =
=
 .
.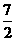
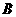 .
.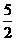
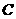 .3
.3 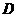 .2
.2
【答案】:C
【解析】:过Q作QM⊥直线L于M,∵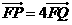
∴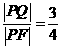 ,又
,又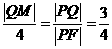 ,∴
,∴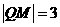 ,由抛物线定义知
,由抛物线定义知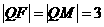
选C
11.已知函数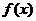 =
=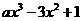 ,若
,若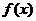 存在唯一的零点
存在唯一的零点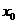 ,且
,且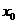 >0,则
>0,则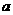 的取值范围为
的取值范围为
 .(2,+∞)
.(2,+∞) 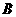 .(-∞,-2)
.(-∞,-2)  .(1,+∞)
.(1,+∞)  .(-∞,-1)
.(-∞,-1)
【答案】:B
【解析1】:由已知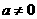 ,
,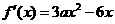 ,令
,令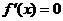 ,得
,得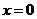 或
或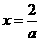 ,
,
当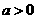 时,
时,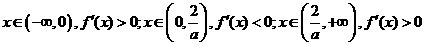 ;
;
且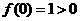 ,
,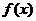 有小于零的零点,不符合题意。
有小于零的零点,不符合题意。
当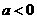 时,
时,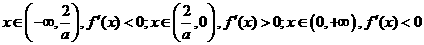
要使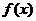 有唯一的零点
有唯一的零点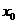 且
且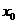 >0,只需
>0,只需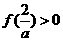 ,即
,即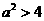 ,
,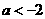 .选B
.选B
【解析2】:由已知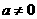 ,
,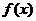 =
=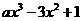 有唯一的正零点,等价于
有唯一的正零点,等价于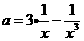
有唯一的正零根,令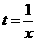 ,则问题又等价于
,则问题又等价于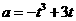 有唯一的正零根,即
有唯一的正零根,即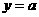 与
与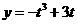 有唯一的交点且交点在在y轴右侧记
有唯一的交点且交点在在y轴右侧记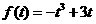 ,
,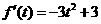 ,由
,由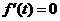 ,
,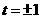 ,
,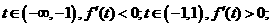 ,
,
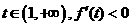 ,要使
,要使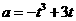 有唯一的正零根,只需
有唯一的正零根,只需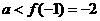 ,选B
,选B
_ueditor_page_break_tag_12.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为
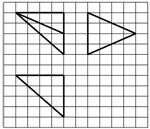
 .
.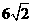
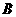 .
.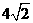
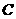 .6
.6  .4
.4
【答案】:C
【解析】:如图所示,原几何体为三棱锥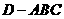 ,
,
其中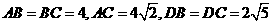 ,
,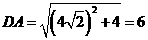 ,故最长的棱的长度为
,故最长的棱的长度为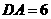 ,选C
,选C
第Ⅱ卷
本卷包括必考题和选考题两个部分。第(13)题-第(21)题为必考题,每个考生都必须作答。第(22)题-第(24)题为选考题,考生根据要求作答。
二.填空题:本大题共四小题,每小题5分。
13.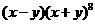 的展开式中
的展开式中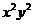 的系数为___________.(用数字填写答案)
的系数为___________.(用数字填写答案)
【答案】: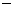 20
20
【解析】: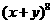 展开式的通项为
展开式的通项为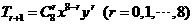 ,
,
∴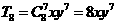 ,
,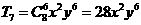
∴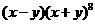 的展开式中
的展开式中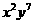 的项为
的项为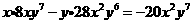 ,故系数为
,故系数为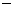 20。
20。
14.甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一个城市.
由此可判断乙去过的城市为_________.
【答案】:A
【解析】:∵丙说:三人同去过同一个城市,甲说没去过B城市,乙说:我没去过C城市
∴三人同去过同一个城市应为A,∴乙至少去过A,若乙再去城市B,甲去过的城市至多两个,不可能比乙多,∴可判断乙去过的城市为A.
15.已知A,B,C是圆O上的三点,若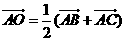 ,则
,则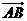 与
与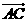 的夹角为_________.
的夹角为_________.
【答案】: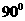
【解析】:∵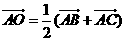 ,∴O为线段BC中点,故BC为
,∴O为线段BC中点,故BC为 的直径,
的直径,
∴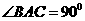 ,∴
,∴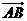 与
与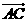 的夹角为
的夹角为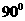 。
。
16.已知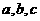 分别为
分别为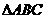 的三个内角
的三个内角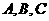 的对边,
的对边,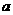 =2,且
=2,且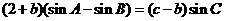 ,则
,则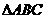 面积的最大值为_________.
面积的最大值为_________.
【答案】: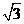
【解析】:由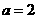 且
且 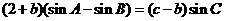 ,
,
即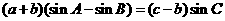 ,由及正弦定理得:
,由及正弦定理得: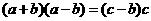
∴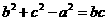 ,故
,故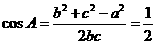 ,∴
,∴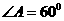 ,∴
,∴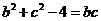
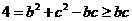 ,∴
,∴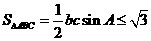 ,
,
三.解答题:解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)已知数列{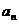 }的前
}的前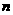 项和为
项和为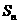 ,
,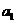 =1,
=1,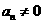 ,
,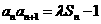 ,其中
,其中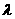 为常数.
为常数.
(Ⅰ)证明: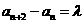 ;
;
(Ⅱ)是否存在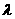 ,使得{
,使得{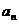 }为等差数列?并说明理由.
}为等差数列?并说明理由.
【解析】:(Ⅰ)由题设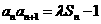 ,
,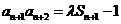 ,两式相减
,两式相减
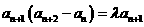 ,由于
,由于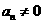 ,所以
,所以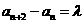 …………6分
…………6分
(Ⅱ)由题设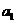 =1,
=1,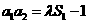 ,可得
,可得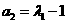 ,由(Ⅰ)知
,由(Ⅰ)知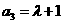
假设{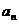 }为等差数列,则
}为等差数列,则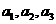 成等差数列,∴
成等差数列,∴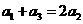 ,解得
,解得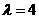 ;
;
证明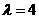 时,{
时,{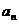 }为等差数列:由
}为等差数列:由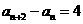 知
知
数列奇数项构成的数列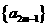 是首项为1,公差为4的等差数列
是首项为1,公差为4的等差数列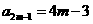
令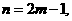 则
则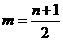 ,∴
,∴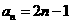
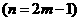
数列偶数项构成的数列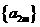 是首项为3,公差为4的等差数列
是首项为3,公差为4的等差数列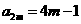
令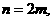 则
则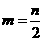 ,∴
,∴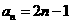
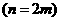
∴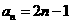 (
(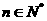 ),
),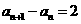
因此,存在存在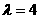 ,使得{
,使得{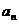 }为等差数列. ………12分
}为等差数列. ………12分
18. (本小题满分12分)从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
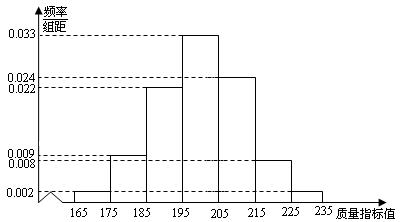
(Ⅰ)求这500件产品质量指标值的样本平均数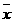 和样本方差
和样本方差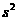 (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,这种产品的质量指标值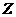 服从正态分布
服从正态分布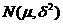 ,其中
,其中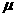 近似为样本平均数
近似为样本平均数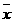 ,
,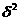 近似为样本方差
近似为样本方差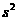 .
.
(i)利用该正态分布,求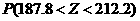 ;
;
(ii)某用户从该企业购买了100件这种产品,记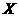 表示这100件产品中质量指标值为于区间(187.8,212.2)的产品件数,利用(i)的结果,求
表示这100件产品中质量指标值为于区间(187.8,212.2)的产品件数,利用(i)的结果,求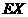 .
.
附: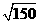 ≈12.2.
≈12.2.
若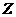 ~
~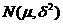 ,则
,则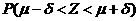 =0.6826,
=0.6826,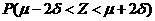 =0.9544.
=0.9544.
【解析】:(Ⅰ) 抽取产品质量指标值的样本平均数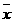 和样本方差
和样本方差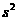 分别为
分别为
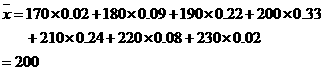
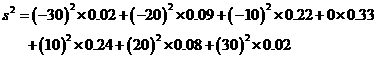
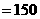 …………6分
…………6分
(Ⅱ)(ⅰ)由(Ⅰ)知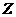 ~
~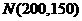 ,从而
,从而
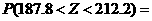
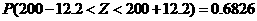 ………………9分
………………9分
(ⅱ)由(ⅰ)知,一件产品中质量指标值为于区间(187.8,212.2)的概率为0.6826
依题意知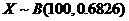 ,所以
,所以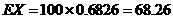 ………12分
………12分
19. (本小题满分12分)如图三棱柱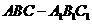 中,侧面
中,侧面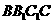 为菱形,
为菱形,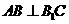 .
.
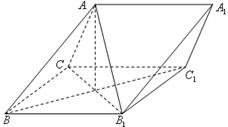 (Ⅰ) 证明:
(Ⅰ) 证明: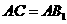 ;
;
(Ⅱ)若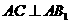 ,
,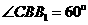 ,AB=BC
,AB=BC
求二面角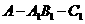 的余弦值.
的余弦值.
【解析】:(Ⅰ)连结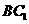 ,交
,交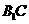 于O,连结AO.因为侧面
于O,连结AO.因为侧面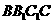 为菱形,所以
为菱形,所以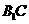
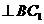 ,且O为
,且O为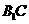 与
与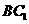 的中点.又
的中点.又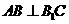 ,所以
,所以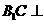 平面
平面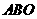 ,故
,故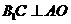 又
又 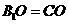 ,故
,故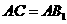 ………6分
………6分
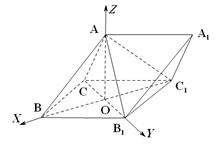
(Ⅱ)因为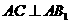 且O为
且O为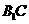 的中点,所以AO=CO 又因为AB=BC,所以
的中点,所以AO=CO 又因为AB=BC,所以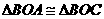
故OA⊥OB,从而OA,OB,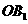 两两互相垂直.
两两互相垂直.
以O为坐标原点,OB的方向为x轴正方向,OB为单位长,建立如图所示空间直角坐标系O-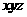 . 因为
. 因为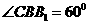 ,所以
,所以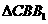 为等边三角形.又AB=BC,则
为等边三角形.又AB=BC,则
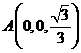 ,
,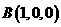 ,
,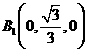 ,
,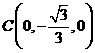
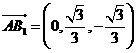 ,
,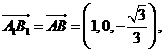
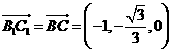
设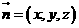 是平面的法向量,则
是平面的法向量,则
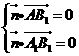 ,即
,即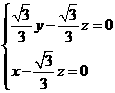 所以可取
所以可取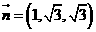
设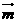 是平面的法向量,则
是平面的法向量,则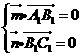 ,同理可取
,同理可取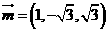
则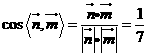 ,所以二面角
,所以二面角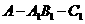 的余弦值为
的余弦值为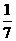 .
.
20. (本小题满分12分) 已知点 (0,-2),椭圆
(0,-2),椭圆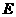 :
: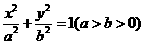 的离心率为
的离心率为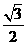 ,
,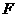 是椭圆的焦点,直线
是椭圆的焦点,直线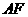 的斜率为
的斜率为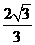 ,
, 为坐标原点.
为坐标原点.
(Ⅰ)求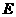 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线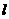 与
与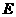 相交于
相交于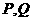 两点,当
两点,当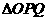 的面积最大时,求
的面积最大时,求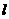 的方程.
的方程.
【解析】:(Ⅰ) 设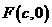 ,由条件知
,由条件知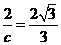 ,得
,得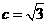 又
又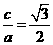 ,
,
所以a=2,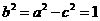 ,故
,故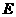 的方程
的方程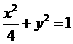 . ……….6分
. ……….6分
(Ⅱ)依题意当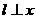 轴不合题意,故设直线l:
轴不合题意,故设直线l: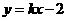 ,设
,设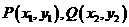
将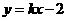 代入
代入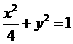 ,得
,得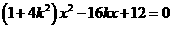 ,
,
当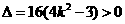 ,即
,即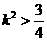 时,
时,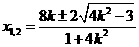
从而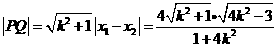
又点O到直线PQ的距离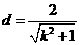 ,所以
,所以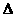 OPQ的面积
OPQ的面积
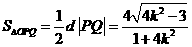 ,
,
设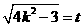 ,则
,则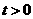 ,
,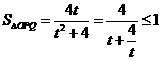 ,
,
当且仅当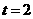 ,
,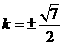 等号成立,且满足
等号成立,且满足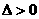 ,所以当
,所以当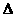 OPQ的面积最大时,
OPQ的面积最大时,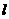 的方程为:
的方程为: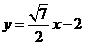 或
或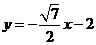 . …………………………12分
. …………………………12分
21. (本小题满分12分)设函数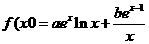 ,曲线
,曲线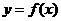 在点(1,
在点(1,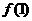 处的切线为
处的切线为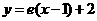 . (Ⅰ)求
. (Ⅰ)求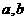 ; (Ⅱ)证明:
; (Ⅱ)证明: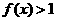 .
.
【解析】:(Ⅰ) 函数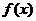 的定义域为
的定义域为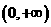 ,
,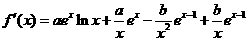
由题意可得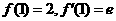 ,故
,故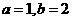 ……………6分
……………6分
(Ⅱ)由(Ⅰ)知,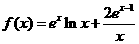 ,从而
,从而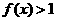 等价于
等价于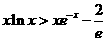
设函数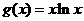 ,则
,则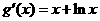 ,所以当
,所以当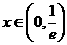 时,
时,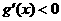 ,当
,当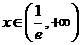 时,
时,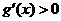 ,故
,故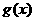 在
在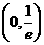 单调递减,在
单调递减,在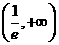 单调递增,从而
单调递增,从而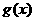 在
在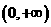 的最小值为
的最小值为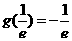 . ……………8分
. ……………8分
设函数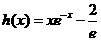 ,则
,则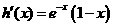 ,所以当
,所以当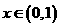 时,
时,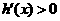 ,当
,当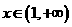 时,
时,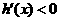 ,故
,故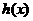 在
在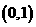 单调递增,在
单调递增,在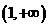 单调递减,从而
单调递减,从而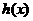
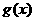 在
在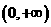 的最小值为
的最小值为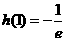 .
.
综上:当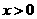 时,
时,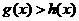 ,即
,即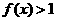 . ……………12分
. ……………12分
请考生从第(22)、(23)、(24)三题中任选一题作答。注意:只能做所选定的题目。如果多做,则按所做的第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的 方框涂黑。
22.(本小题满分10分)选修4—1:几何证明选讲
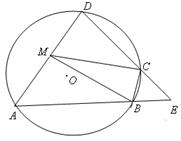
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE
.(Ⅰ)证明:∠D=∠E;

(Ⅱ)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.
【解析】:.(Ⅰ) 由题设知得A、B、C、D四点共圆,所以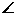 D=
D=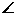 CBE,由已知得,
CBE,由已知得,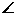 CBE=
CBE=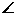 E ,
E ,
所以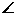 D=
D=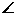 E ……………5分
E ……………5分
(Ⅱ)设BCN中点为,连接MN,则由MB=MC,知MN⊥BC 所以O在MN上,又AD不是O的直径,M为AD中点,故OM⊥AD, 即MN⊥AD,所以AD//BC,故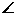 A=
A=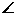 CBE, 又
CBE, 又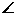 CBE=
CBE=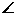 E,故
E,故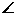 A=
A=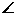 E由(Ⅰ)(1)知
E由(Ⅰ)(1)知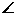 D=
D=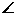 E, 所以△ADE为等边三角形. ……………10分
E, 所以△ADE为等边三角形. ……………10分
23. (本小题满分10分)选修4—4:坐标系与参数方程
已知曲线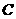 :
: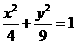 ,直线
,直线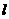 :
: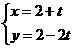 (
(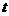 为参数).
为参数).
(Ⅰ)写出曲线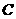 的参数方程,直线
的参数方程,直线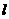 的普通方程;
的普通方程;
(Ⅱ)过曲线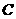 上任一点
上任一点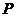 作与
作与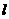 夹角为
夹角为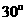 的直线,交
的直线,交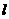 于点
于点 ,求
,求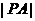 的最大值与最小值.
的最大值与最小值.
【解析】:.(Ⅰ) 曲线C的参数方程为: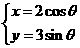 (
(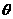 为参数),
为参数),
直线l的普通方程为: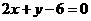 ………5分
………5分
(Ⅱ)(2)在曲线C上任意取一点P (2cos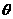 ,3sin
,3sin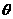 )到l的距离为
)到l的距离为
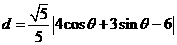 ,
,
则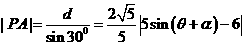 ,其中
,其中 为锐角.且
为锐角.且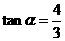 .
.
当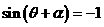 时,
时,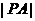 取得最大值,最大值为
取得最大值,最大值为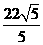 ;
;
当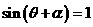 时,
时,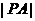 取得最小值,最小值为
取得最小值,最小值为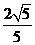 . …………10分
. …………10分
24. (本小题满分10分)选修4—5:不等式选讲
若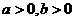 ,且
,且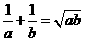 .
.
(Ⅰ) 求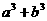 的最小值;
的最小值;
(Ⅱ)是否存在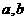 ,使得
,使得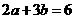 ?并说明理由.
?并说明理由.
【解析】:(Ⅰ) 由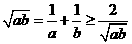 ,得
,得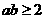 ,且当
,且当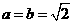 时等号成立,
时等号成立,
故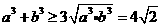 ,且当
,且当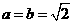 时等号成立,
时等号成立,
∴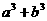 的最小值为
的最小值为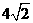 . ………5分
. ………5分
(Ⅱ)由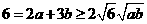 ,得
,得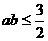 ,又由(Ⅰ)知
,又由(Ⅰ)知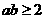 ,二者矛盾,
,二者矛盾,
所以不存在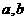 ,使得
,使得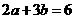 成立. ……………10分
成立. ……………10分


