(单词翻译:单击)
一、 选择题(每小题3分,共24分).
1. 的倒数为( )
的倒数为( )
A.  B.
B. 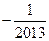 C. 2013 D.
C. 2013 D. 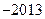
2.运用湘教版初中数学教材上使用的某种电子计算器求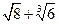 的近似值,其按键顺序正确的是( )
的近似值,其按键顺序正确的是( )
A.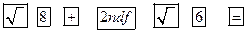
B. 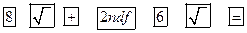
C. 
D. 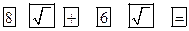
3.下列几何体中,其主视图不是中心对称图形的是( )
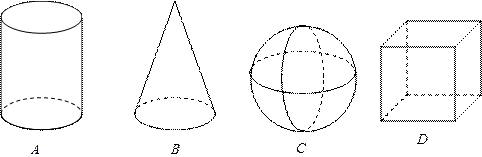
4.如图,下列条件中能判定直线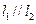 的是( )
的是( )
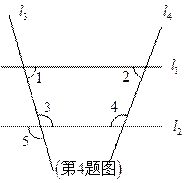
A.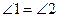 B.
B. 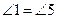
C.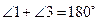 D.
D. 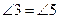
5.实数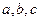 在数轴上对应的点如图所示,则下列式子中正确的是( )
在数轴上对应的点如图所示,则下列式子中正确的是( )
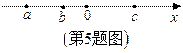
A.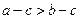 B.
B. 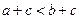
C.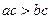 D.
D. 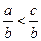
6.已知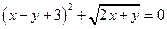 ,则
,则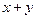 的值为
的值为
A. 0 B. 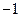 C. 1 D. 5
C. 1 D. 5
7.下列说法正确的是( )
A. 一组数据2,5,3,1,4,3的中位数是3
B. 五边形的外角和是540度
C. “菱形的对角线互相垂直”的逆命题是真命题
D. 三角形的外心是这个三角形三条角平分线的交点
8.我们知道,一元二次方程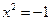 没有实数根,即不存在一个实数的平方等于
没有实数根,即不存在一个实数的平方等于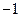 .
.
若我们规定一个新数“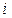 ”,使其满足
”,使其满足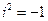 (即方程
(即方程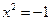 有一个根为
有一个根为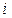 )。并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有
)。并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有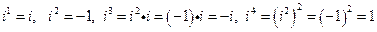 ,
,
从而对于任意正整数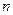 ,我们可以得到
,我们可以得到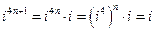 , 同理可得
, 同理可得
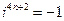 ,
, 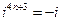 ,
, 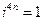 .那么
.那么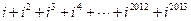 的值为( )
的值为( )
A. 0 B. 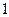 C.
C.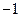 D.
D. 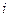
二、填空题(每小题3分,共24分)
9.钓鱼岛列岛是我国固有领土,共由8个岛屿组成,其中最大的岛是钓鱼岛,面积约为4.3平方公里,最小的岛是飞濑屿,面积约为0.0008平方公里.请用科学计数法表示飞濑屿的面积约为 平方公里.
10.一副扑克牌52张(不含鬼牌),分为黑桃、红心、方块、及梅花4种花色,每种花色各有13张,分别标有字母A、K、Q、J和数字10、9、8、7、6、5、4、3、2.从这副牌中任意抽取一张,则这张牌是标有字母的概率是
11.已知一次函数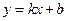 的图象经过A(
的图象经过A(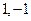 ),B(
),B(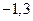 )两点,则
)两点,则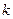 0
0
(填“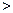 ”或“
”或“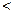 ”)
”)
12.定义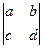 为二阶行列式.规定它的运算法则为
为二阶行列式.规定它的运算法则为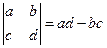 .那么当
.那么当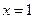 时,二阶行列式
时,二阶行列式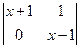 的值为 .
的值为 .
13.如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=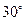 ,则∠B= 度.
,则∠B= 度.
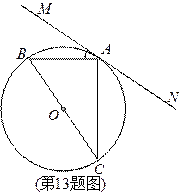
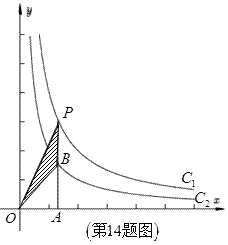
14.如图,两个反比例函数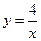 和
和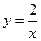 在第一象限内的图象分别是
在第一象限内的图象分别是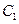 和
和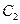 ,设点P在
,设点P在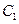 上,
上,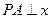 轴于点A,交
轴于点A,交 于点B,则△POB的面积为
于点B,则△POB的面积为
15.已知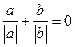 ,则
,则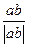 的值为
的值为
16.电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,此WORD中为方便大家识别与印刷,我还是把图乙中的0都标出来吧,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有 .(请填入方块上的字母)
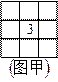 | 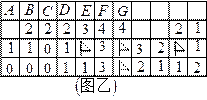 | ||
三、 解答题(本大题共9个小题,共72分)
17.(本小题6分)计算: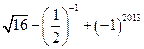
18. (本小题6分)解不等式组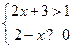 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
19. (本小题6分)先化简,再求值: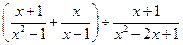 其中
其中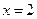 .
.
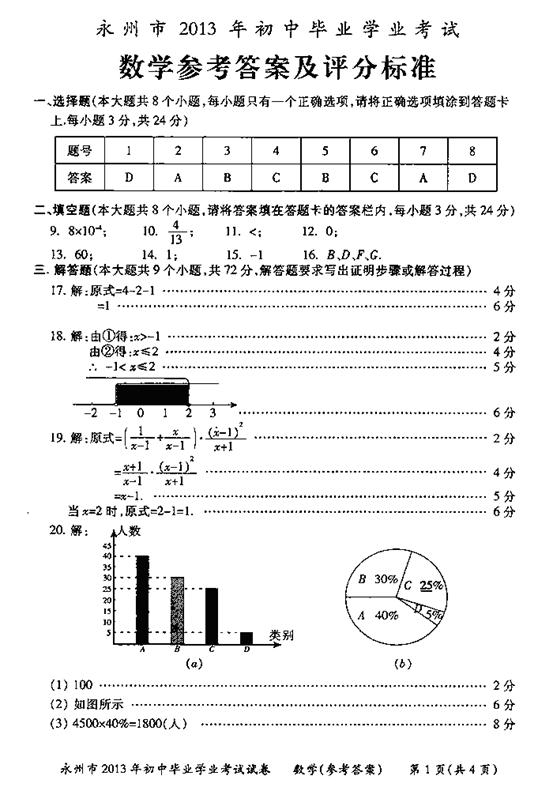
20. (本小题8分)某县为了了解2013年初中毕业生毕业后的去向,对部分初三学生进行了抽样调查,就初三学生的四种去向(A. 读普通高中; B. 读职业高中 C. 直接进入社会就业; D.其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).
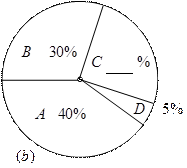
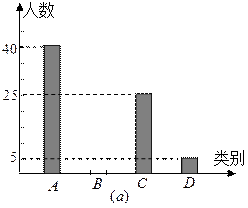
请问:
(1)该县共调查了 名初中毕业生
(2)将两幅统计图中不完整的部分补充完整;
(3)若该县2013年初三毕业生共有4500人,请估计该县今年的初三毕业生中读普通高中的学生人数.
21. (本小题8分)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN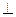 AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
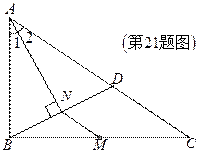
(1)求证:BN=DN
(2)求△ABC的周长.
22.(本小题8分)中国现行的个人所得税法自2011年9月1日起施行,其中规定个人所得税纳税办法如下:
一.以个人每月工资收入额减去3500元后的余额作为其每月应纳税所得额;
二.个人所得税纳税税率如下表所示
纳税级数 | 个人每月应纳税所得额 | 纳税税率 |
1 | 不超过1500元的部分 | 3% |
2 | 超过1500元至4500元的部分 | 10% |
3 | 超过4500元至9000元的部分 | 20% |
4 | 超过9000元至35000元的部分 | 25% |
5 | 超过35000元至55000元的部分 | 30% |
6 | 超过55000元至80000元的部分 | 35% |
7 | 超过80000元的部分 | 45% |
(1)若甲、乙两人的每月工资收入额分别为4000元和6000元,请分别求出甲、乙两人的每月应缴纳的个人所得税;
(2)若丙每月缴纳的个人所得税为95元,则丙每月的工资收入额应为多少?
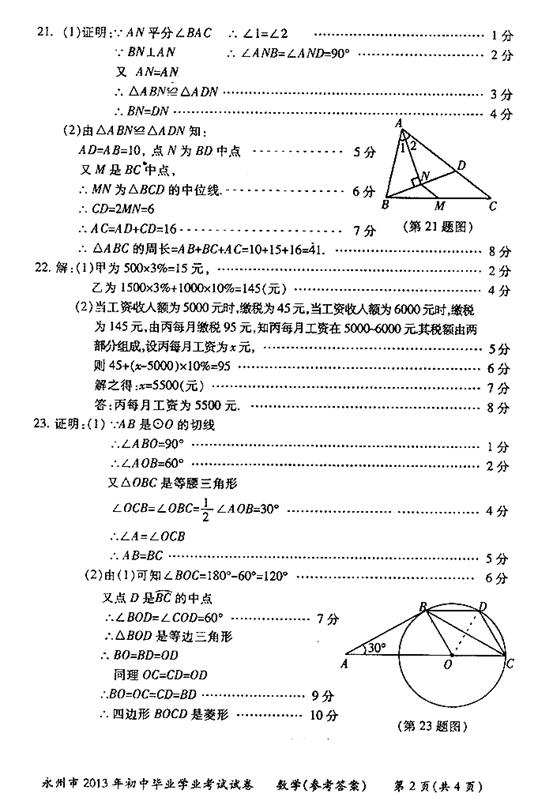
23.(本小题10分)如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=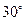 ,D为
,D为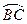 的中点.
的中点.
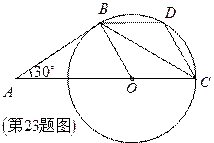
(1)求证:AB=BC
(2)求证:四边形BOCD是菱形..
24.(本小题10分)如图,已知二次函数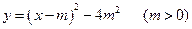 的图象与
的图象与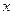 轴交于A、B两点.
轴交于A、B两点.
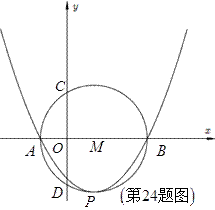
(1)写出A、B两点的坐标(坐标用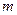 表示)
表示)
(2)若二次函数图象的顶点P在以AB为直径的圆上,求二次函数的解析式
(3)设以AB为直径的⊙M与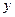 轴交于C、D两点,求CD的长.
轴交于C、D两点,求CD的长.
25.(本小题10分)如图,已知AB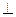 BD,CD
BD,CD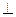 BD
BD
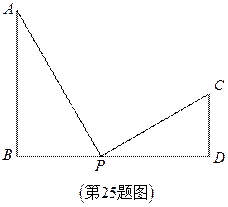
(1)若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;若不存在,请说明理由;
(2)若AB=9,CD=4,BD=12,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(3)若AB=9,CD=4,BD=15,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(4)若AB=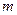 ,CD=
,CD=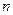 ,BD=
,BD=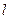 ,请问
,请问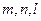 满足什么关系时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点?两个P点?三个P点?
满足什么关系时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点?两个P点?三个P点?