(单词翻译:单击)
一、选择题(本大题共20小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分)
1.在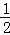 ,0,﹣1,﹣
,0,﹣1,﹣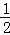 这四个数中,最小的数是( )
这四个数中,最小的数是( )
A.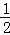 B.0 C.﹣
B.0 C.﹣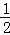 D.﹣1
D.﹣1
2.下列运算,正确的是( )
A.4a﹣2a=2 B.a6÷a3=a2 C.(﹣a3b)2=a6b2 D.(a﹣b)2=a2﹣b2
3.下列几何体,主视图和俯视图都为矩形的是( )

A. B. C. D.
4.PM2.5是指大气中直径≤0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )
A.2.5×10﹣7 B. 2.5×10﹣6 C. 25×10﹣7 D. 0.25×10﹣5
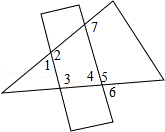
5.如图,把一直尺放置在一个三角形纸片上,则下列结论正确的是( )
A.∠1+∠6>180° B.∠2+∠5<180° C.∠3+∠4<180° D.∠3+∠7>180°
(5题图) (8题图)
6.下列四个 图形:
图形:

其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B.2 C.3 D.4
7.方程5x+2y=﹣9与下列方程构成的方程组的解为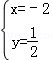 的是( )
的是( )
A.x+2y=1 B. 3x+2y=﹣8 C.5x+4y=﹣3 D.3x﹣4y=﹣8
3x+2y=﹣8 C.5x+4y=﹣3 D.3x﹣4y=﹣8
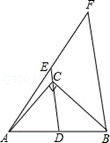
8.如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=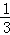 CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为( )
CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为( )
A.6 B.7 C.8 D.10
9.以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩/分 | 80 | 85 | 90 | 95 |
人数/人 | 1 | 2 | 5 | 2 |
则这组数据的中位数和平均数分别为( )
A.90,90 B.90,89 C.85,89 D.85,90
10.在△ABC和△A1B1C1中,下列四个命题:
(1)若AB=A1B1,AC=A1C1,∠A=∠A1,则△ABC≌△A1B1C1;
(2)若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;
(3)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(4)若AC:A1C1=CB:C1B1,∠C=∠C 1,则△ABC∽△A1B1C1.
1,则△ABC∽△A1B1C1.
其中真命题的个数为( )
A.4个 B.3个 C.2个 D.1个
11.在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,则两次摸出的小球的标号之和大于4的概率是( )2m
A.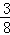 B.
B.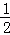 C.
C.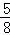 D.
D.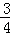
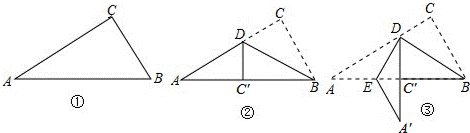
12.如图①是一个直角三角形纸片,∠A=30°,BC=4cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,则折痕DE的长为( )21·cn·jy·com
A.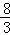 cm B.2
cm B.2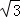 cm C.2
cm C.2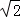 cm D.3cm
cm D.3cm
13.某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15
C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
14.如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
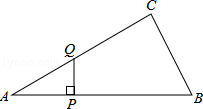
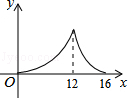
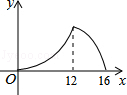
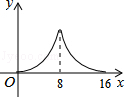
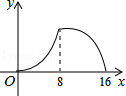
A. B. C. D.
15.若不等式组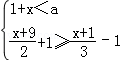 有解,则实数a的取值范围是( )
有解,则实数a的取值范围是( )
A.a<﹣36 B.a≤﹣36 C.a>﹣36 D.a≥﹣36
16.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为( )
A.10° B.20° C.7.5° D.15°
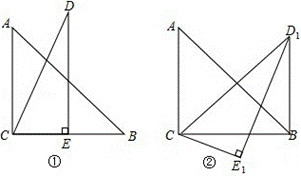
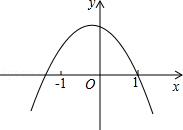
(16题图) (17题图)
17.已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=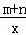 的图象可能是( )
的图象可能是( )
A.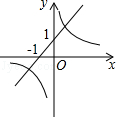 B.
B.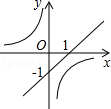 C.
C.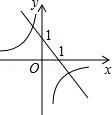 D.
D.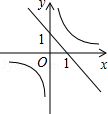
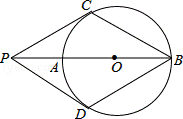
18.如图,P为⊙O 的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.其中正确的个数 为( )
为( )
A.4个 B.3个 C.2个 D.1个
(18题图) (19题图)
19.如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(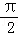 ﹣1)cm2 B.(
﹣1)cm2 B.(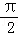 +1)cm2 C.1cm2 D.
+1)cm2 C.1cm2 D.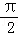 cm2
cm2
20.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:21教育名师原创作品
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,满分12分。只要求填写最后结果,每小题填对得3分)
21.化简(1+ )÷
)÷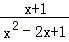 的结果为 _________ .
的结果为 _________ .
22.七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用水量x/m3 | 0 | 5<x≤10 | 10<x≤15 | 15<x≤20 | x>20 |
频数/户 | 12 | 20 | 3 | ||
频率 | 0.12 | 0.07 |
若该小区有800户家庭,据此估计该小区月均用水量不超过10m3的家庭约有 _________ 户.
23.如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则sinα的值为 _________ .
.

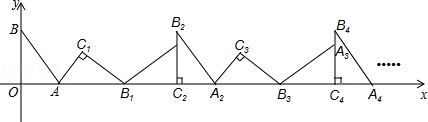
24.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ,0),B(0,4),则点B2014的横坐标为 _________ .
,0),B(0,4),则点B2014的横坐标为 _________ .
三、解答题(本大题共5 小题,满分48分。解答应写出必要的文字说明、证明过程或推演步骤)
小题,满分48分。解答应写出必要的文字说明、证明过程或推演步骤)
25.(8分)某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克 按售价的8折售完.
按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
26.(8分)如图①,△OAB中,A(0,2),B(4,0),将△AOB向右平移m个单位,得到△O′A′B′.
(1)当m=4时,如图②.若反比例函数y= 的图象经过点A′,一次函数y=ax+b的图象经过A′、B′两点.求反比例函数及一次函数的表达式;
的图象经过点A′,一次函数y=ax+b的图象经过A′、B′两点.求反比例函数及一次函数的表达式;
(2)若反比例函数y= 的图象经过点A′及A′B′的中点M,求m的值.
的图象经过点A′及A′B′的中点M,求m的值.

27.(10分)如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.

28.(11分)如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
(1)求证: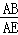 =
= ;
;
(2)若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形.

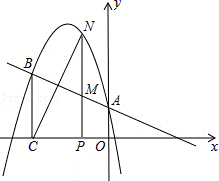
29.(11分)二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣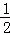 x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
 (1)求二次函数的表达式;
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
2014年山东泰安市学生学业水平测试数学试题参考答案
一、选择题(本大题共20小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分)
 1.D.2.C.3.D.4.B. 5.D. 6.C. 7.D. 8.C. 9.B. 10.B. 11.C.
1.D.2.C.3.D.4.B. 5.D. 6.C. 7.D. 8.C. 9.B. 10.B. 11.C.
12.A. 13.A. 14.B. 15.C.16.D. 17.C. 18.A. 19.A. 20.B.
二、填空题(本大题共4小题,满分12分。只要求填写最后结果,每小题填对得3分)
21. x﹣1 .22. 560 .23.  .24. 10070 .
.24. 10070 .
三、解答题(本大题共5小题,满分48分。解答应写出必要的文字说明、证明过程或推演步骤)
25.解:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元,
由题意 ,得
,得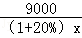 =2×
=2×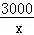 +300,解得x=5,经检验x=5是方程的解.
+300,解得x=5,经检验x=5是方程的解.
答:该种干果的第一次进价是每千克5元;
(2)[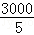 +
+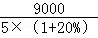 ﹣600]×9+600×9×80%﹣(3000+9000)
﹣600]×9+600×9×80%﹣(3000+9000)
=(600+1500﹣600)×9+4320﹣12000
=1500×9+4320﹣12000
=13500+4320﹣12000
=5820(元).
答:超 市销售这种干果共盈利5820元.
市销售这种干果共盈利5820元.
26. 解:(1)由图②值:A′点的坐标为:(4,2),B′点的坐标为:(8,0),
∴k=4×2=8,∴y= ,
,
把(4,2),(8,0)代入y=ax+b得:
 ,解得:
,解得: ,
,
∴经过A′、B′两点的一次函数表达式为:y=﹣ x+4;
x+4;
(2)当△A OB向右平移m个单位时,A′点的坐标为:(m,2),B′点的坐标为:(m+4,0)
OB向右平移m个单位时,A′点的坐标为:(m,2),B′点的坐标为:(m+4,0)
则A′B′的中点M的坐标为 :(m+4﹣2,1)
:(m+4﹣2,1)
∴2m=m+2,解得:m=2,
∴当m=2时,反比例函数y= 的图象经过点A′及A′B′的中点M.
的图象经过点A′及A′B′的中点M.
27.(1)证明:∵△ADE是等腰直角三角形,F是AE中点,∴DF⊥AE,DF=AF=EF,
又∵∠ABC=90°,∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF,
在△DFC和△AFM中,
 ,∴△DFC≌△AFM(AAS),∴CF=MF,∴∠FMC=∠FCM;
,∴△DFC≌△AFM(AAS),∴CF=MF,∴∠FMC=∠FCM;
(2)AD⊥MC,理由:由(1)知,∠MFC=90°,FD=EF,FM=FC,
∴∠FDE=∠FMC=45°,∴DE∥CM,∴AD⊥MC.
28.证明:(1)∵AB=AD,∴∠ADB=∠ABE,
又∵∠ADB=∠ACB,∴∠ABE=∠ACB,
又∵∠BAE=∠CAB,∴△ABE∽△ACB,∴ =
=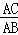 ,又∵AB=AD,∴
,又∵AB=AD,∴ =
= ;
;
(2)设AE=x,∵AE:EC=1:2,∴EC=2x,
由(1)得:AB2=AE•AC,∴AB=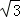 x,
x,
又∵BA⊥AC,∴BC=2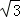 x,∴∠ACB=30°,
x,∴∠ACB=30°,
∵F是BC中点,∴BF=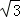 x,∴BF=AB=AD,
x,∴BF=AB=AD,
又∵∠ADB=∠ACB=∠ABD,∴∠ADB=∠CBD=30°,∴AD∥BF,
∴四边形ABFD是平行四边形,
又∵AD=AB,∴四边形ABFD是菱形.
29.解:(1)由题设可知A(0,1),B(﹣3, ),
),
根据题意得: ,解得:
,解得: ,则二次函数的解析式是:y=﹣
,则二次函数的解析式是:y=﹣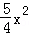 ﹣
﹣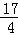 x+1;
x+1;
(2)设N(x,﹣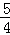 x2﹣
x2﹣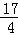 x+1),则M、P点的坐标分别是(x,﹣
x+1),则M、P点的坐标分别是(x,﹣ x+1),(x,0).
x+1),(x,0).
∴MN=PN﹣PM
=﹣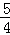 x2﹣
x2﹣ x+1﹣(﹣
x+1﹣(﹣ x+1)
x+1)
 =﹣
=﹣ x2﹣
x2﹣ x
x
=﹣ (x+
(x+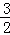 )2+
)2+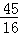 ,
,
则当x=﹣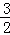 时,MN的最大值为
时,MN的最大值为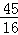 ;
;
(3)连接MN、BN、BM与NC互相垂直平分,
即四边形BCMN是菱形,
由于BC∥MN,
即MN=BC,且BC=MC,
即﹣ x2﹣
x2﹣ x=
x= ,且(﹣
,且(﹣ x+1)2+(x+3)2=
x+1)2+(x+3)2= ,
,
解得:x=1,
故当N(﹣1,4)时,MN和NC互相垂直平分.


