(单词翻译:单击)
第Ⅰ卷
一、选择题(本题满分24分,共有8道小题,每小题3分)
下列每小题都给出标号为A、B、C、D的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.
1.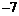 的绝对值是().
的绝对值是().
A.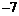 B.7C.
B.7C.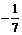 D.
D.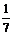
2.下列四个图形中,既是轴对称图形又是中心对称图形的是().

A. B. C. D.
3.据统计,我国2013年全年完成造林面积约6090000公顷.6090000用科学记数法可表示为().
A.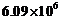 B.
B.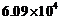 C.
C.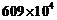 D.
D.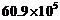
4.在一个有15万人的小镇,随机调查了3000人,其中有300人看中央电视台的早间新闻.据 此,估计该镇看中央电视台早间新闻的约有().
此,估计该镇看中央电视台早间新闻的约有().
A.2.5万人B.2万人C.1.5万人D.1万人
5.已知⊙O1与⊙O2的半径分别是2和4,O1O2=5,则⊙O1与⊙O2的位置关系是().
A.内含B.内 切 C.相交 D.外切
切 C.相交 D.外切
6.某工程队准备修建一条长1200m的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快20%,结果提前2天完成任务.若设原计划每天修建道路xm,则根据题意可列方程为().
A.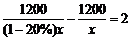 B.
B.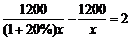
C.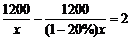 D.
D.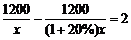
7.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为().
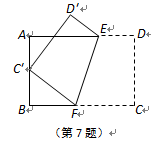
A.4 B.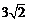
C.4.5 D.5
8.函数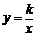 与
与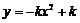 (
(
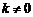 )在同一直角坐标系中的图象可能是().
)在同一直角坐标系中的图象可能是().

A. B. C. D.
第Ⅱ卷
二、填空题(本题满分18分,共有6道小题,每小题3分)
9.计算: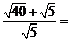 .
.
10.某茶厂用甲、乙两台分装机分装某种茶叶(每袋茶叶的标准质量为200g).为了监控分装质量,该厂从它们各自分装的茶叶中随机抽取了50袋,测得它们的实际质量分析如下:
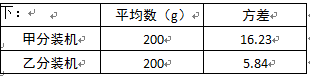
则这两台分装机中,分装的茶叶质量更稳定的是(填“甲”或“乙”).
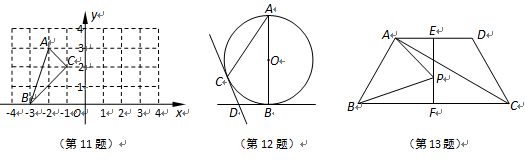
11.如图,△ABC的顶点都在方格线的交点(格点)上,如果将△ABC绕C点按逆时针方向旋转90°,那么点B的对应点B′的坐标是.
12.如图, AB是⊙O的直径,BD,CD分别
AB是⊙O的直径,BD,CD分别 是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是°.
是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是°.
13.如图,在等腰梯形ABCD中,AD=2,∠BCD=60°,对角线AC平分∠BCD, E,F分别是底边AD,BC的中点,连接EF.点P是EF上的任意一点,连接PA,PB,则PA+PB的最小值为.
14.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改 变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要个小立方块.
变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要个小立方块.
主视图 左视图 俯视图
三、作图题(本题满分4分)
用圆规、直尺作图,不写作法,但要保留作图痕迹.
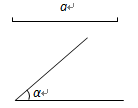
15.已知:线段a,∠α.
求作:△ABC,使AB=AC=a,∠B=∠α.
四、解答题(本题满分74分,共有9道小题)
16.(本小题满分8分,每题4分 )
)
(1)计算: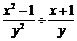 ; (2)解不等式组:
; (2)解不等式组: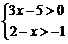
17.(本小题满分6分)
空气质量状况已引起全社会的广泛关注,某市统计了2013年每月空气质量达到良好以上的天数,整理后制成如下折线统计图和扇形统计图.
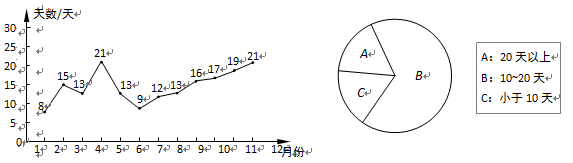
根据以上信息解答下列问题:
(1)该市2013年每月空气质量达到良好以上天数的中位数是_____天,众数是_____天;
(2)求扇形统计图中扇形A的圆心角的度数;
(3)根据以上统计图提供的信息,请你简要分析该市的空气质量状况(字数不超过30字).
18.(本小题满分6分)
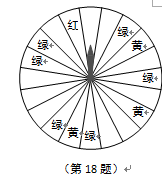
某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
19.(本小题满分6分)
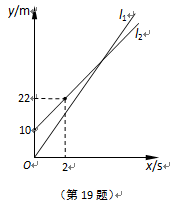
甲、乙两人进行赛跑,甲比乙跑得快,现在甲让乙先跑10米,甲再起跑.图中l1和l2分别表示甲、乙两人跑步的路程y(m)与甲跑步的时间x (s)之间的函数关系,其中l1的关系式为y1=8x,问甲追上乙用了多长时间?
(s)之间的函数关系,其中l1的关系式为y1=8x,问甲追上乙用了多长时间?
20.(本小题满分8分)
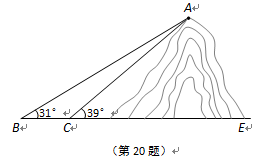
如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.
(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(结果精确到0.1m).
(参考数据:tan31° ≈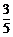 ,sin31° ≈
,sin31° ≈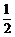 ,tan39°≈
,tan39°≈ ,sin39°≈
,sin39°≈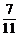 )
)
21.(本小题满分8分)
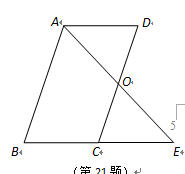
已知:如图,□ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B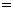 ∠AEB
∠AEB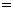 °时,四边形ACED是正方形?请说明理由.
°时,四边形ACED是正方形?请说明理由.
22.(本小题满分10分)
某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件, 而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与 销售单价x(元)之间的函数关系式;
销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
青岛市二○一四年初中学生学业考试
数学试题参考答案及评分标准
一、选择题(本题满分24分,共有8道小题,每小题3分)
题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答 案 | B | D | A | C | C | D | A | B |
二、填空题(本题满分18分,共有6道小题,每小题3分 )
9.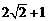 10.乙
10.乙
11.(1,0) 12.35
13.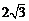 14.54
14.54
三、作图题(本题满分4分)
15.正确作图;3分
正确写出结论.4分
四、解答题(本题满分74分,共有9道小题)
16.(本小题满分8分)
(1)解:原式=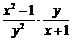
=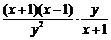
=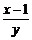 .4分
.4分
| ①② |
(2)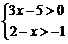
解:解不等式①,得
x>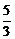 .
.
解不等式②,得
x<3.
所以,原不等式组的解集是
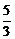 <x<3.4分
<x<3.4分
17. (本小题满分6分)
解:(1)14,13. 2分
(2)360°×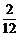 =60°,
=60°,
答:扇形A的圆心角的度数是60°. 4分
(3)合理 即可.6分
即可.6分
18. (本小题满分6分)
解:(1)P(转动一次转盘获得购物券)=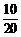 =
=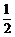 .2分
.2分
(2)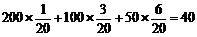 (元)
(元)
∵40元>30元,
∴选择转转盘对顾客更合算.6分
19. (本小题满分6分)
解:设y2=kx+b(k≠0),
根据题意,可得方程组
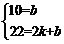 |
解这个方程 组,得
组,得
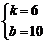 |
所以y2=6x+10.
当y1=y2时,8x=6x+10,
解这个方程,得x=5.
答:甲追上乙用了5s.6分
20. (本小题满分8分)
解:(1)过点A作AD⊥BE于D,
设山AD的高度为x m,
在Rt△ABD中,∠ADB=90°,
tan31°=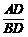 ,
,
∴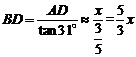 .
.
在Rt△ACD中,∠ADC=90°,
tan39°=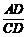 ,
,
∴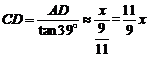 .
.
∵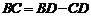
∴ 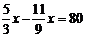 ,
,
解这个方程,得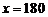 .
.
即山的高度为180米. 6分
(2)在Rt△ACD中,∠ADC=90°,
sin39°=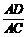 ,
,
∴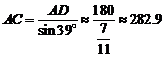 (米).
(米).
答:索道AC长约为282.9米. . 8分
21. (本小题满分8分)
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
又∵OC=OD,
∴△AOD≌△EOC.
4分
(2)当∠B=∠AEB=45°时,四边形ACED是正方形.
∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵∠B=∠AEB= 45°,
45°,
∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.
∴□ACED是菱形.
∵AB=AE,AB=CD,
∴AE=CD.
∴菱形ACED是正方形. 8分
22. (本小题满分10分)
解:(1)y=(x-50)[50+5(100-x)]
=(x-50)(-5x+550)
=-5x2+800x-27500
∴y=-5x2+800x-27500.4分
(2)y=-5x2+800x-27500
=-5(x-80)2+4500
∵a=-5<0,
∴抛物线开口向下.
∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,y最大值=4500.6分
(3)当y=4000时,-5(x-80)2+4500=4000,
解这个方程,得x1=70,x2=90.
∴当70≤x≤90时,每天的销售利润 不低于4000元.
不低于4000元.
由每天的总成本不超过7000元,得50(-5x+550)≤7000,
解这个不等式,得x≥82.∴82≤x≤90,
∵50≤x≤100,∴销售单价应该控制在82元至90元之间. 10分


