(单词翻译:单击)









南通市2014年中考数学试卷最后一题解析
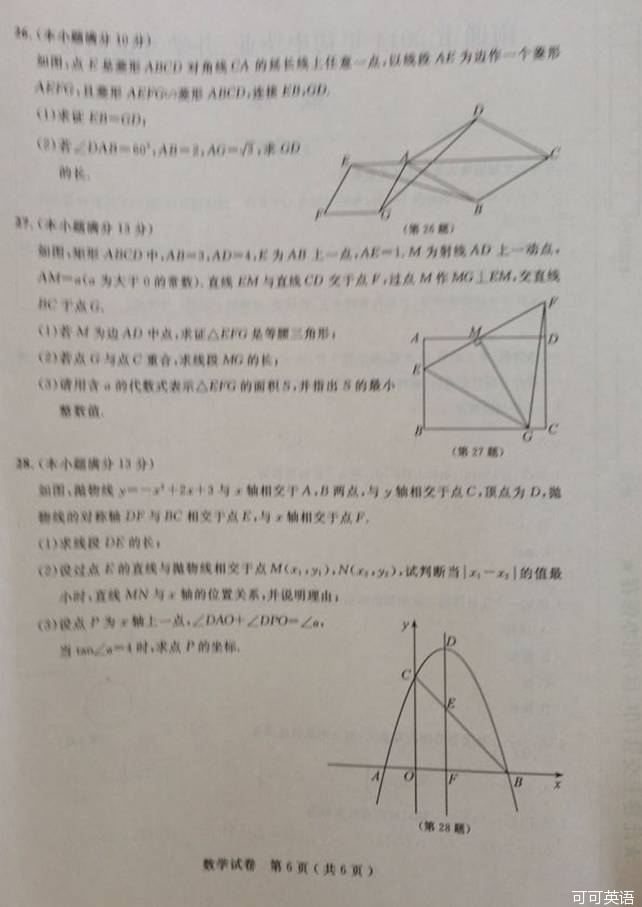
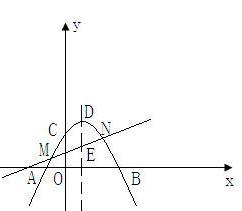
【试题】如图,抛物线y=-x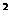 +2x+3与x轴相交于A、B两点,与y轴交于C,顶点为D,对称轴与BC交于E.
+2x+3与x轴相交于A、B两点,与y轴交于C,顶点为D,对称轴与BC交于E.
(1) 求DE的长,
(2) 设过E的直线与抛物线y=-x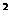 +2x+3与x轴相交于M(x
+2x+3与x轴相交于M(x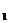 ,y
,y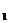 ),N(x
),N(x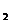 ,y
,y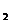 )试判断当
)试判断当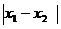 的值最小时,直线MN与x轴的位置关系,
的值最小时,直线MN与x轴的位置关系,
(3) 设P为x轴上的一点,∠DAO+∠DPO=∠α,当tan∠α=4时,求P的坐标.
【解析】(1)略
(2)∵E的坐标为(1,2)∴用待定系数法得直线MN的解析式为y=(2-b)x+b
点M,N的坐标是方程组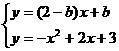 的解,用代入法将方程组化为关于x的一元二次方程,得x
的解,用代入法将方程组化为关于x的一元二次方程,得x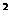 -bx+b-3=0,由韦达定理得,x
-bx+b-3=0,由韦达定理得,x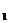 + x
+ x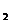 =b,x
=b,x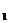 x
x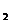 = b-3,
= b-3,
∵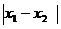 =
=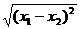 =
=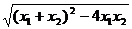 =
=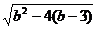 =
=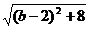 ,
,
∴当b=2时,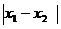 最小值=2
最小值=2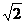 .∵b=2,∴直线MN的解析式为y=2,∴直线MN∥x轴.
.∵b=2,∴直线MN的解析式为y=2,∴直线MN∥x轴.
(4) 有三种解法:
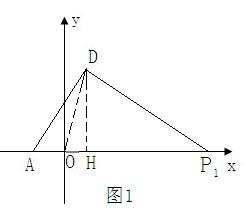
① 如图1,这里数学机智灵活的同学易发现tan∠DOH=4,又∵tan∠α=4,∴∠DOH=∠α,应用三角形外角定理与∠DAO+∠DPO=∠α,得∠DPO=∠ADO,显然△ADP∽△AOD,从而得AD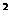 =AO·AP
=AO·AP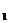 ,而AD
,而AD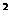 =20,AO=1,因此AP
=20,AO=1,因此AP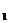 =20,∴OP
=20,∴OP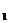 =19,由对称性OP
=19,由对称性OP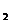 =17,∴P
=17,∴P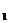 (19,0) P
(19,0) P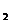 (-17,0)
(-17,0)
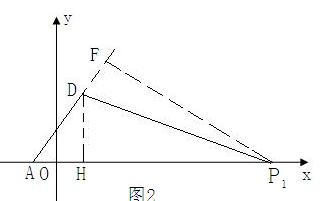
②③如图2,应用三角形外角定理转化出∠α.延长AD,过P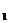 作P
作P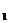 F⊥AF于F,显然∠FD P
F⊥AF于F,显然∠FD P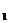 =∠α,AD=2
=∠α,AD=2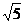 ,∵tan∠α=4,设DF=m,则P
,∵tan∠α=4,设DF=m,则P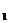 F=4m,△ADH∽△A P
F=4m,△ADH∽△A P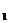 F,则
F,则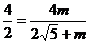
解得m=2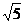 ,∴AF=4
,∴AF=4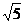 ,P
,P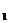 F=8
F=8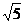 ,在直角三角形AF P
,在直角三角形AF P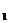 中由勾股定理得,AP
中由勾股定理得,AP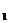 =20,
=20,
以下与方法①相同.
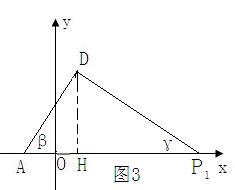
③如图3,如果高中生来解很简单,应用三角公式tan(β+γ)=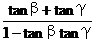
∵∠α=∠β+∠γ,tan∠α=4,tan∠β=2 tan∠γ=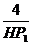 ,将以上条件代入三角公式tan(β+γ)=
,将以上条件代入三角公式tan(β+γ)=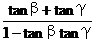 ,可解得H P
,可解得H P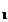 =18,以下与方法①相同.
=18,以下与方法①相同.