(单词翻译:单击)
一、选择题:每题给出的四个选项中,只有一个选项符合题意要求,请将正确选项填涂到机读卡上相应的位置(本大题共10个小题,每小题3分,共30分)
1.(3分)(2014•广安)﹣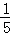 的相反数是( )
的相反数是( )
A.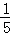 B. ﹣
B. ﹣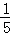 C. 5 D. ﹣5
C. 5 D. ﹣5
考点: 相反数.
分析: 求一个数的相反数,即在这个数的前面加负号.
解答: 解:﹣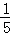 的相反数是
的相反数是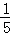 .
.
故选A.
点评: 本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号.一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.学生易把相反数的意义与倒数的意义混淆.
2.(3分)(2014•广安)下列运算正确的是( )
A. (﹣a2)•a3=﹣a6 B. x6÷x3=x2 C. |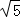 ﹣3|=
﹣3|=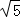 ﹣3 D. (a2)3=a6
﹣3 D. (a2)3=a6
考点: 同底数幂的除法;实数的性质;同底数幂的乘法;幂的乘方与积的乘方.
分析: 分别进行积的乘方和幂的乘方、同底数幂的乘法、同底数幂的除法、绝对值的化简等运算,然后选择正确答案.
解答: 解:A、(﹣a2)•a3=﹣a5,故本选项错误;
B、x6÷x3=x3,故本选项错误;
C、|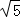 ﹣3|=3﹣
﹣3|=3﹣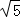 ,故本选项错误;
,故本选项错误;
D、(a2)3=a6,故本选项正确.
故选D.
点评: 本题考查了积的乘方和幂的乘方、同底数幂的乘法、同底数幂的除法、绝对值的化简等知识,掌握运算法则是解答本题的关键.
3.(3分)(2014•广安)参加广安市2014年高中阶段教育学生招生考试的学生大约有4.3万人,将4.3万人用科学记数法表示应为( )
A. 4.3×104人 B. 43×105人 C. 0.43×10 5人 D. 4.3×105人
5人 D. 4.3×105人
考点: 科学记数法—表示较大的数.
分析: 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答: 解:4.3万=4 3000=4.3×104,
故选:A.
点评: 此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(3分)(2014•广安)我市某校举办“行为规范在身边”演讲比赛中,7位评委给其中一名选手的评分(单位:分)分别为:9.25,9.82,9.45,9.63,9.57,9.35,9.78.则这组数据的中位数和平均数分别是( )
A. 9.63和9.54 B. 9.57和9.55 C. 9.63和9.56 D. 9.57和9.57
考 点: 中位数;算术平均数.
点: 中位数;算术平均数.
分析: 根据中位数和平均数的概念求解.
解答: 解:这组数据按照从小到大的顺序排列为:9.25, 9.35,9.45,9.57,9.63,9.78,9.82,
9.35,9.45,9.57,9.63,9.78,9.82,
则中位数为:9.57,
平均数为: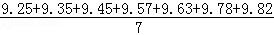 =9.55.
=9.55.
故选B.
点评: 本题考查了中位数和平均数的知识,平均数是指在一组数据中所有数据之和再除以数据的个数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
5.(3分)(2014•广安)要使二次根式 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
 A. x=
A. x=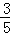 B. x≠
B. x≠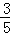 C. x≥
C. x≥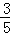 D. x≤
D. x≤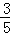
考点: 二次根式有意义的条件.
分析: 根据二次根式有意义的条件可得5x﹣3≥0,再解不等式即可.
解答: 解:由题意得:5x﹣3≥0,
解得:x≥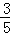 ,
,
故选:C.
点评: 此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.
6.(3分)(2014•广安)下列说法正确的是( )
A. 为了了解全国中学生每天体育锻炼的时间,应采用普查的方式
B. 若甲组数据的方差S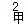 =0.03,乙组数据的方差是S
=0.03,乙组数据的方差是S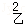 =0.2,则乙组数据比甲组数据稳定
=0.2,则乙组数据比甲组数据稳定
C. 广安市明天一定会下雨
D. 一组数据4、5、6、5、2、8的众数是5
考点: 全面调查与抽样调查;众数;方差;随机事件
分析: A.根据普查的意义判断即可;
B.方差越小越稳定;
C.广安市明天会不会下雨不确定;
D.根据众数的定义判断即可.
解答: 解:A.了解全国中学生每天体育锻炼的时间,由于人数较多,应当采用抽样调查,故本选项错误;
B.甲的方差小于乙的方差所以甲组数据比乙组数据稳定,故本选项错误;
C.广安市明天一定会下雨,不正确;
D.数据4、5、6、5、2、8中5的个数最多,所以众数为5,故本项正确.
故选:D.
点评: 本题主要考查了全面调查、方差、众数的意义.
7.(3分)(2014•广安)如图所示的几何体的俯视图是( )

A.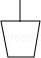 B.
B. C.
C. D.
D.
考点: 简单几何体的三视图.
分析: 找到从上面看所得到的图形即可.
解答: 解:该几何体的俯视图为: .
.
故选D.
点评: 本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
8.(3分)(2014•广安)如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=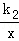 (k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为( )
(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为( )
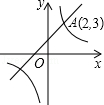
A. y1>y2 B. y1=y2 C. y1<y2 D. 以上说法都不对
D. 以上说法都不对
考点: 反比例函数与一次函数的交点问题.
分析: 根据两函数的交点坐标,结合图象得出答案即可.
解答: 解:∵两图象都经过点A(2,3),
∴根据图象当x>2时,y1>y2,
故选A.
点评: 本题考查了一次函数和反比例函数的交点问题的应用,主要考查学生的理解能力和观察图象的能力,题目比较典型,难度不大.
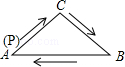
9.(3分)(2014•广安)如图,在△ABC中,AC=BC,有一动点P从点A出发,沿A→C→B→A匀速运动.则CP的长度s与时间t之间的函数关系用图象描述大致是( )
A.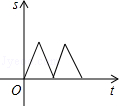 B.
B.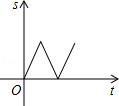 C.
C.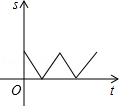 D.
D.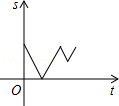
考点: 动点问题的函数图象
分析: 该题属于分段函数:点P在边AC上时,s随t的增大而减小;当点P在边BC上时,s随t的增大而增大;当点P在线段BD上时,s随t的增大而减小;当点P在线段AD上时,s随t的增大而增大.
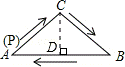
解答: 解:如图,过点C作CD⊥AB于点D.
∵在△ABC中,AC=BC,
∴AD=BD.
①点P在边AC上时,s随t的增大而减小.故A、B错误;
②当点P在边BC上时,s随t的增大而增大;
③当点P在线段BD上时,s随t的增大而减小,点P与点D重合时,s最小,但是不等于零.故C错误;
④当点P在线段AD上时,s随t的增大而增大.故D正确.
故选:D.
点评: 本题考查了动点问题的函数图象.用图象解决问题时,要理清图象的含义即会识图.
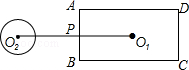
10.(3分)(2014• 广安)如图,矩形ABCD的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现( )
广安)如图,矩形ABCD的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现( )
A. 3次 B. 4次 C. 5次 D. 6次
考点: 直线与圆的位置关系.
分析: 根据题意作出图形,直接写出答案即可.
解答: 解:如图:,⊙O2与矩形的边只有一个公共点的情况一共出现4次,
故选B.
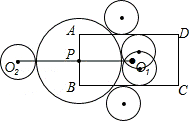
点评: 本题考查了直线与圆的位置关系,解题的关键是了解当圆与直线相切时,点到圆心的距离等于圆的半径.
二、填空题:请把最简答案直接填写在题目后的横线上(本大题共6个小题,每小题3分,共18分)
11.(3分)(2014•广安)直线y=3x+2沿y轴向下平移5个单位,则平移后直线与y轴的交点坐标为 (0,﹣3) .
考点: 一次函数图象与几何变换.
分析: 先由直线直线y=3x+2沿y轴向下平移5个单位可得y=3x﹣3,再根据一次函数y=kx+b与y轴交点为(0,b)可得答案.
解答: 解:直线直线y=3x+2沿y轴向下平移5个单位可得y=3x+2﹣5,
即y=3x﹣3,
则平移后直线与y轴的交点坐标为:(0,﹣3).
故答案为:(0,﹣3).
点评: 此题主要考查了一次函数图象的几何变换,关键是掌握直线y=kx+b沿y轴平移后,函数解析式的k值不变,b值上移加、下移减.
12.(3分)(2014•广安)分解因式:my2﹣9m= m(y+3)(y﹣3) .
考点: 提公因式法与公式法的综合运用.
分析: 首先提取公因式m,进而利用平方差公式进行分解即可.
解答: 解:my2﹣9m=m(y2﹣9)=m(y+3)(y﹣3).
故答案为:m(y+3)(y﹣3).
点评: 此题主要考查了提取公因式法和公式法分解因式,熟练掌握平方差公式是解题关键.
13.(3分)(2014•广安)化简(1﹣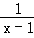 )÷
)÷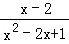 的结果是 x﹣1 .
的结果是 x﹣1 .
考点: 分式的混合运算
分析: 根据 分式混合运算的法则进行计算即可.
分式混合运算的法则进行计算即可.
解答: 解:原式=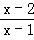 •
•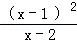
=x﹣1.
故答案为:x﹣1.
点评: 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键
14.(3分)(2014•广安)若∠α的补角为76°28′,则∠α= 103°32′ .
考点: 余角和补角;度分秒的换算.
分析: 根据互为补角的概念可得出∠α=180°﹣76°28′.
解答: 解:∵∠α的补角为76°28′,
∴∠α=180°﹣76°28′=103°32′,
故答案为103°32′.
点评: 本题考查了余角和补角以及度分秒的换算,是基础题,要熟练掌握.
15.(3分)(2014•广安)一个多边形的内角和比四边形内角和的3倍多180°,这个多边形的边数是 9 .
考点: 多边形内角与外角
分析: 多边形的外角和是360度,多边形的外角和是内角和的3倍多180 °,则多边形的内角和是360×3+180°度,再由多边形的内角和列方程解答即可.
°,则多边形的内角和是360×3+180°度,再由多边形的内角和列方程解答即可.
解答: 解:设这个多边形的边数是n,由题意得,
(n﹣2)×180°=360°×3+180°
解得n=9.
故答案为:9.
点评: 本题主要考查了多边形的内角和定理与外角和定理,熟练掌握定理是解题的关键.
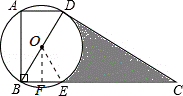
16.(3分)(2014•广安)如图,在直角梯形ABCD中,∠ABC=90°,上底AD为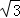 ,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,且∠ABD为30°.则图中阴影部分的面积为
,以对角线BD为直径的⊙O与CD切于点D,与BC交于点E,且∠ABD为30°.则图中阴影部分的面积为 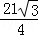 ﹣π (不取近似值).
﹣π (不取近似值).
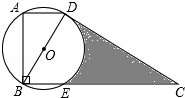
考点: 切线的性质;直角梯形;扇形面积的计算.
分析: 连接OE,根据∠ABC=90°,AD=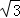 ,∠ABD为30°,可得出AB与BD,可证明△OBE为等边三角形,即可得出∠C=30°.阴影部分的面积为直角梯形ABCD的面积﹣三角形ABD的面积﹣三角形OBE的面积﹣扇形ODE的面积.
,∠ABD为30°,可得出AB与BD,可证明△OBE为等边三角形,即可得出∠C=30°.阴影部分的面积为直角梯形ABCD的面积﹣三角形ABD的面积﹣三角形OBE的面积﹣扇形ODE的面积.
解答: 解:连接OE,过点O作OF⊥BE于点F.
∵∠ABC=90°,AD=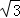 ,∠ABD为30°,
,∠ABD为30°,
∴BD=2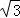 ,
,
∴AB=3,
∵OB=OE,
∴∠DBC=60°,
∴OF=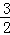 ,
,
∵CD为⊙O的切线,
∴∠BDC=90°,
∴∠C=30°,
∴BC=4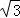 ,
,
S阴影=S梯形ABCD﹣S△ABD﹣S△OBE﹣S扇形ODE
=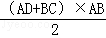 ﹣
﹣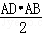 ﹣
﹣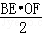 ﹣
﹣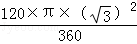
=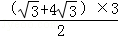 ﹣
﹣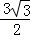 ﹣
﹣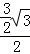 ﹣π
﹣π
=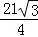 ﹣π.
﹣π.
故答案为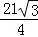 ﹣π.
﹣π.
点评: 本题考查了切线的性质、直角梯形以及扇形面积的计算,要熟悉扇形的面积公式.
三、解答题(本大题共4个小题,第17小题5分,第18、19、20小题各6分,共23分)
17.(5分)(2014•广安)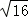 +(﹣
+(﹣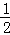 )﹣1+(
)﹣1+(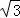 ﹣5)0﹣
﹣5)0﹣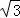 cos30°.
cos30°.
考点: 实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值
专题: 计算题.
分析: 原式第一项利用平方根定义化简,第二项利用负指数幂法则计算,第三项利用零指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果.
解答: 解:原式=4﹣2+1﹣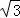 ×
×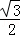
=4﹣2+1﹣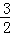
=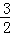 .
.
点评: 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
18.(6分)(2014•广安)解不等式组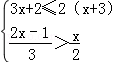 ,并写出不等式组的整数解.
,并写出不等式组的整数解.
考点: 解一元一次不等式组;一元一次不等式组的整数解.
分析: 首先分别解出两个不等式的解集,再根据大小小大中间找确定不等式组的解集,然后再根据x的取值范围找出整数解.
解答: 解: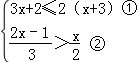 ,
,
解①得:x≤4,
解②得:x>2,
不等式组的解集为:2<x≤4.
则不等式组的整数解:3,4.
点评: 此题主要考查了解一元一次不等式组,以及不等式组的整数解,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
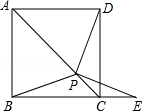
19.(6分)(2014•广安)如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC.
考点: 全等三角形的判定与性质;正方形的性质.
专题: 证明题.
分析: 根据正方形的四条边都相等可得BC=CD,对角线平分一组对角可得∠BCP=∠DCP,再利用“边角边”证明△BCP和△DCP全等,根据全等三角形对应角相等可得∠PDC=∠PBC,再根据等边对等角可得∠PBC=∠PEC,从而得证.
解答: 证明:在正方形ABCD中,BC=CD,∠BCP=∠DCP,
在△BCP和△DCP中,
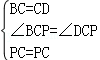 ,
,
∴△BCP≌△DCP(SAS),
∴∠PDC=∠PBC,
∵PB=PE,
∴∠PBC=∠PEC,
∴∠PDC=∠PEC.
点评: 本题考查了全等三角形的判定与性质,正方形的性质,等边对等角的性质,熟记各性质并判断出全等三角形是解题的关键.
20.(6分)(2014•广安)如图,反比例函数y=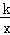 (k为常数,且k≠0)经过点A(1,3).
(k为常数,且k≠0)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.
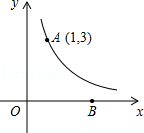
考点: 待定系数法求反比例函数解析式;待定系数法求一次函数解析式
分析: (1)利用待定系数法把A(1,3)代入反比例函数y=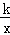 可得k的值,进而得到解析式;
可得k的值,进而得到解析式;
(2)根据△AOB的面积为6求出B点坐标,再设直线AB的解析式为y=kx+b,把A、B两点代入可得k、b的值,进而得到答案.
解答: 解:(1)∵反比例函数y=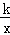 (k为常数,且k≠0)经过点A(1,3),
(k为常数,且k≠0)经过点A(1,3),
∴3=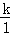 ,
,
解得:k=3,
∴反比例函数解析式为y=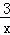 ;
;
(2)设B(a,0),则BO=a,
∵△AOB的面积为6,
∴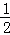 •a•3=6,
•a•3=6,
解得:a=4,
∴B(4,0),
设直线AB的解析式为y=kx+b,
∵经 过A(1,3)B(4,0),
过A(1,3)B(4,0),
∴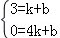 ,
,
解得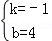 ,
,
∴直线AB的解析式为y=﹣x+4.
点评: 此题主要考查了待定系数法求一次函数解析式和反比例函数解析式,关键是正确确定出B点坐标.
四、实践应用:本大题共4个小题,第21题6分,第23、24、25题各8分,共30分)
21.(6分)(2014•广安)大课间活动时,有两个同学做了一个数字游戏:有三张正面写有数字﹣1,0,1的卡片,它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值,然后将卡片放回并洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q值,两次结果记为(p,q).
(1)请你帮他们用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0没有实数解的概率.
考点: 列表法与树状图法;根的判别式
分析: (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)可求得满足关于x的方程x2+px+q=0没有实数解的有:(﹣1,1),(0,1),(1,1),再利用概率公式即可求得答案.
解答: 解:(1)画树状图得:
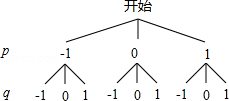
则共有9种等可能的结果;
(2)由(1)可得:满足关于x的方程 x2+px+q=0没有实数解的有:(﹣1,1),(0,1),(1,1),
x2+px+q=0没有实数解的有:(﹣1,1),(0,1),(1,1),
∴满足关于x的方程x2+px+q=0没有实数解的概率为: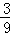 =
=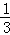 .
.
点评: 本题考查的是用列表法或画树 状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
22.(8分)(2014•广安)广安某水果点计划购进甲、乙两种新出产的水果共140千克,这两种水果的进价、售价如表所示:
进价(元/千克) | 售价(元/千克) | |
甲种 | 5 | 8 |
乙种 | 9 | 13 |
(1)若该水果店预计进货款为1000元,则这两种水果各购进多少千克?
(2)若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,应怎样安排进货才能使水果点在销售完这批水果时获利最多?此时利润为多少元?
考点: 一次函数的应用;二元一次方程组的应用.
分析: (1)根据计划购进甲、乙两种新出产的水果共140千克,进而利用该水果店预计进货款为1000元,得出等式求出即可;
(2)利用两种水果每千克的利润,进而表示出总利润,进而利用一次函数增减性得出即可.
解答: 解:(1)设购进甲种水果x千克,则购进乙种水果(140﹣x)千克,根据题意可得:
5x+9 (140﹣x)=1000,
(140﹣x)=1000,
解得:x=65,
∴140﹣x=75(千克),
答:购进甲种水果65千克,乙种水果75千克;
(2)由图表可得:甲种水果每千克利润为:3元,乙种水果每千克利润为:4元,
设总利润为W,由题意可得出:W= 3x+4(140﹣x)=﹣x+560,
3x+4(140﹣x)=﹣x+560,
故W随x的增大而减小,则x越小W越大,
因为该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,
∴140﹣x≤3x,
解得:x≥35,
∴当x=35时,W最大=﹣35+560=525(元),
故140﹣35=105(kg).
答:当甲购进35千克,乙种水果105千克时,此时利润最大为525元.
点评: 主要考查了一次函数的应用以及一元一次不等式的应用和一元 一次方程的应用等知识,利用一次函数增减性得出函数最值是解题关键.
一次方程的应用等知识,利用一次函数增减性得出函数最值是解题关键.
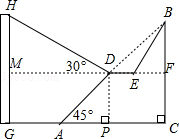
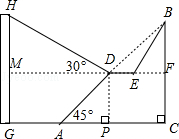
23.(8分)(2014•广安)为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB长60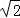 米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
(1)若修建的斜坡BE的坡比为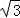 :1,求休闲平台DE的长是多少米?
:1,求休闲平台DE的长是多少米?
(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G,H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
考点: 解直角三角形的应用-坡度坡角问题.
分析: (1)由三角函数的定义,即可求得DF与BF的长,又由坡度的定义,即可求得EF的长,继而求得平台DE的长;
(2)首先设GH=x米,在Rt△DMH中由三角函数的定义,即可求得GH的长.
解答: 解:(1)∵FM∥CG,
∴∠BDF=∠BAC=45°,
∵斜坡AB长60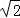 米,D是AB的中点,
米,D是AB的中点,
∴BD=30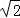 米,
米,
∴DF=BD•cos∠BDF=30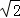 ×
×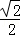 =30(米),BF=DF=30米,
=30(米),BF=DF=30米,
∵斜坡BE的坡比为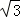 :1,
:1,
∴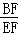 =
=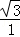 ,
,
解得:EF=10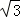 (米),
(米),
∴DE=DF﹣EF=30﹣10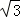 (米);
(米);
答:休闲平台DE的长是(30﹣10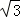 )米;
)米;
(2)设GH=x米,则MH=GH﹣GM=x﹣30(米),DM=AG+AP=33+30=63(米),
在Rt△DMH中,tan30°= ,即
,即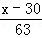 =
=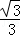 ,
,
解得:x=30+21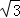 ,
,
答:建筑物GH的高为(30+21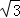 )米.
)米.
点评: 此题考查了坡度坡角问题以及俯角仰角的定义.此题难度较大,注意根据题意构造直角三角形,并解直角三角形;注意掌握数形结合思想与方程思想的应用.
2 4.(8分)(2014•广安)在校园文化建设活动中,需要裁剪一些菱形来美化教室.现有平行四边形ABCD的邻边长分别为1,a(a>1)的纸片,先剪去一个菱形,余下一个四边形,在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,…依此类推,请画出剪三次后余下的四边形是菱形的裁剪线的各种示意图,并求出a的值.
4.(8分)(2014•广安)在校园文化建设活动中,需要裁剪一些菱形来美化教室.现有平行四边形ABCD的邻边长分别为1,a(a>1)的纸片,先剪去一个菱形,余下一个四边形,在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,…依此类推,请画出剪三次后余下的四边形是菱形的裁剪线的各种示意图,并求出a的值.
考点: 作图—应用与设计作图.
分析: 平行四边形ABCD的邻边长分别为1,a(a>1),剪三次后余下的四边形是菱形的4种情况画出示意图.
解答: 解:①如图,a=4,

②如图,a=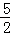 ,
,

③如图,a=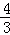 ,
,

④如图,a=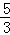 ,
,

点评: 此题主要考查了图形的剪拼以及菱形的判定,根据已知行四边形ABCD将平行四边形分割是解题关键.
五、推理论证(9分)
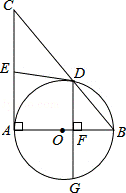
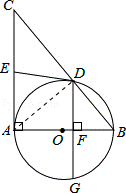
25.(9分)(2014•广安)如图,AB为⊙O的直径,以AB为直角边作Rt△ABC,∠CAB=90°,斜边BC与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥AB于点F,交⊙O于点G.
(1)求证:E是AC的中点;
(2)若AE=3,cos∠ACB=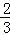 ,求弦DG的长.
,求弦DG的长.
考点: 切线的性质
分析: (1)连AD,由AB为直径,根据圆周角定理得推论得到∠ADB=90°,而∠ACB=90°,根据切线的判定定理得到AC是⊙O的切线,而DE与⊙O相切,根据切线长定理得ED=EA,则∠EDA=∠EAD,利用等角的余角相等可得到∠C=∠CDE,则ED=EC,即可得到EA=EC;
(2)由(1)可得AC=2AE=6,结合cos∠ACB=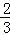 推知sin∠ACB=
推知sin∠ACB=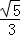 ,然后利用圆周角定理、垂径定理,解直角三角形即可求得DG的长度.
,然后利用圆周角定理、垂径定理,解直角三角形即可求得DG的长度.
解答: (1)证明:连AD,如图
∵AB为⊙O的直径,∠CAB=90°,
∴AC是⊙O的切线,
又∵DE与⊙O相切,
∴ED=EA,
∴∠EAD=∠EDA,
而∠C=90°﹣∠EAD,∠CDE=90°﹣∠EDA,
∴∠C=∠CDE,
∴ED=EC,
∴EA=EC,
即E为BC的中点;
(2)解:由(1)知,E为BC的中点,则AC=2AE=6.
∵cos∠ACB=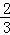 ,∴sin∠ACB=
,∴sin∠ACB= =
=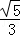 .
.
连接AD,则∠ADC=90°.
在Rt△ACD中,AD=AC•sin∠ACB=6×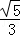 =
=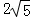 .
.
在Rt△ADF中,DF=AD•sin∠DAF=AD•sin∠ACB=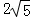 ×
×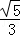 =
=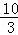 ,
,
∴DG=2DF=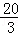 .
.
点评: 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
六、拓展探究(10分)
26.(10分)(2014•广安)如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣4,0),B(﹣1,0)两点.
(1)求抛物线的解析式;
(2)在第三象限的抛物线上有一动点D.
①如图(1),若四边形ODAE是以OA为对角线的平行四边形,当平行四边形ODAE的面积为6时,请判断平行四边形ODAE是否为菱形?说明理由.
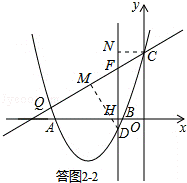
②如图(2),直线y=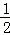 x+3与抛物线交于点Q、C两点,过点D作直线DF⊥x轴于点H,交QC于点F.请问是否存在这样的点D,使点D到直线CQ的距离与点C到直线DF的距离之比为
x+3与抛物线交于点Q、C两点,过点D作直线DF⊥x轴于点H,交QC于点F.请问是否存在这样的点D,使点D到直线CQ的距离与点C到直线DF的距离之比为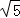 :2?若存在,请求出点D的坐标;若不存在,请说明理由.
:2?若存在,请求出点D的坐标;若不存在,请说明理由.
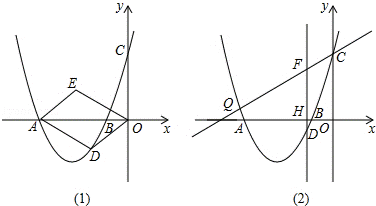
考点: 二次函数综合题
分析: (1)利用待定系数法求出抛物线的解析式;
(2)①本问需结合菱形、平行四边形的性质来进行分析.如答图2﹣1,作辅助线,求出点D的坐标,进而判断平行四边形ODAE是否为菱形;
②本问为存在型问题.如答图2﹣2,作辅助线,构造相似三角形,利用比例式,列出一元二次方程,求得点D的坐标.
解答: 解:(1)把点A(﹣4,0)、B(﹣1,0)代入解析式y=ax2+bx+3,
得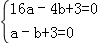 ,解得
,解得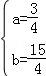 ,
,
∴抛物线的解析式为:y=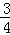 x2+
x2+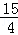 x+3.
x+3.
(2)①如答图2﹣1,过点D作DH⊥x轴于点H.
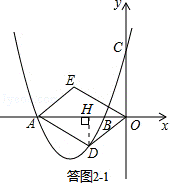
∵S▱ODAE=6,OA=4,
∴S△AOD=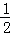 OA•DH=3,
OA•DH=3,
∴DH=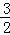 .
.
因为D在第三象限,所以D的纵坐标为负,且D在抛物线上,
∴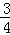 x2+
x2+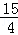 x+3=﹣
x+3=﹣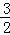 ,
,
解得:x1=﹣2,x2=﹣3.
∴点D坐标为(﹣2,﹣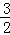 )或(﹣3,﹣
)或(﹣3,﹣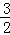 ).
).
当点D为(﹣2,﹣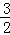 )时,DH垂直平分OA,平行四边形ODAE为菱形;
)时,DH垂直平分OA,平行四边形ODAE为菱形;
当点D为(﹣3,﹣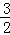 )时,OD≠AD,平行四边形ODAE不为菱形.
)时,OD≠AD,平行四边形ODAE不为菱形.
②假设存在.
如答图2﹣2,过点D作DM⊥CQ于M,过点C作CN⊥DF于N,则DM:CN=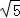 :2.
:2.
设D(m,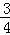 m2+
m2+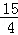 m+3)(m<0),则F(m,
m+3)(m<0),则F(m,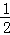 m+3).
m+3).
∴CN=﹣m,NF=﹣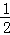 m
m
∴CF=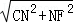 =﹣
=﹣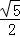 m.
m.
∵∠DMF=∠CNF=90°,∠DFM=∠CFN,
∴△DMF∽△CNF,
∴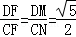 ,
,
∴DF=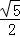 CF=﹣
CF=﹣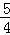 m.
m.
∴DN=NF+DF=﹣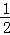 m﹣
m﹣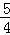 m=﹣
m=﹣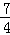 m.
m.
又DN=3﹣(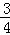 m2+
m2+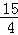 m+3)=﹣
m+3)=﹣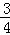 m2﹣
m2﹣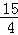 m,
m,
∴﹣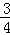 m2﹣
m2﹣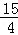 m=﹣
m=﹣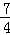 m
m
解得:m=﹣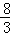 或m=0(舍去)
或m=0(舍去)
∴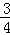 m2+
m2+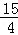 m+3=﹣
m+3=﹣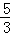
∴D(﹣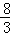 ,﹣
,﹣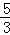 ).
).
综上所述,存在满足条件的点D,点D的坐标为(﹣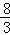 ,﹣
,﹣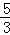 ).
).
点评: 本题为二次函数压轴题,综合考查了二次函数、待定系数法、相似三角形、平行四边形、菱形等知识点.第(2)问涉及存在型问题,有一定的难度.在解题过程中,注意数形结合思想、分类讨论思想及方程思想等的应用.


