(单词翻译:单击)
卷 Ⅰ
说明:本卷共有1大题,10小题,每小题3分,共30分.请用2B铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满.
一、选择题(请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.在数1,0,-1, -2中,最小的数是( )
A.1 B.0 C.-1 D.-2
2.如图,经 过刨平的木板上的两个点,能弹出一条笔直的墨线,而
过刨平的木板上的两个点,能弹出一条笔直的墨线,而
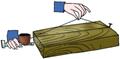
且只能弹出一条墨线.能解释这一实际应用的数学知识是( )
A.两点确定一条直线 B.两点之间线段最短
C.垂线段最短 D.在同一平面内,过一点有且只有一条直线与已知直线垂直
3.一个几何体的三视图如图所示,那么这个几何体是( )
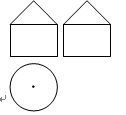
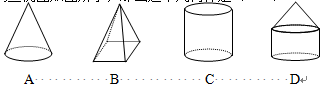
4.一个布袋里装有5个球,其中3个红球,2个白球,每个球除颜色外其他完全相同,从中任意摸出一个球,是红球的概率是( )
A.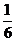 B.
B.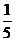
 C.
C.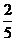 D.
D.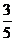
5.在式子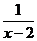 ,
,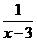 ,
, 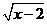 ,
,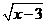 中,x可以取2和3的是( )
中,x可以取2和3的是( )
A.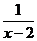 B.
B.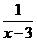 C.
C.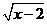 D.
D.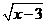
6.如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,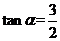 ,则t的值是( )
,则t的值是( )
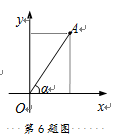
A.1 B.1.5 C.2 D.3
7.把代数式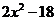 分解因式,结果正确的是( )
分解因式,结果正确的是( )
A.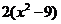 B.
B.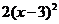 C.
C.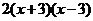 D.
D.
8.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结若∠1=20°,则∠B的度数是( )
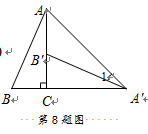
A.70° B.65° C.60° D.55°
9.如图是二次函数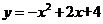 的图象,使
的图象,使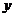 ≤1成立的
≤1成立的
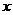 的取值范围是( )
的取值范围是( )

A.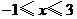 B.
B.
C.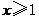 D.
D. 或
或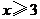
10.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪得一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
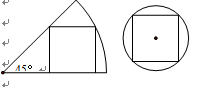
A.5:4 B.5:2 C.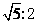 D.
D.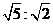
卷 Ⅱ
说明:本卷共有2大题,14小题,共9 0分. 答题请用0.5毫米及以上的黑色签字笔书写在“答题纸”的对应位置上.
0分. 答题请用0.5毫米及以上的黑色签字笔书写在“答题纸”的对应位置上.
二、填空题(本题有6小题,每小题4分,共24分)
11.写出一个解为x≥1的一元一次不等式__________ .
12.分式方程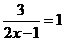 的解是_________.
的解是_________.
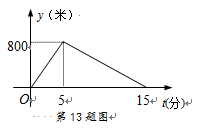
13.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行_________米.
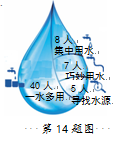
14.小亮对60名同学进行节水方法选择的问卷调查(每人选择一项),人数统计如图,如果绘制成扇形统计图,那么表示“一水多用”的扇形圆心角的度数是_________.
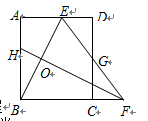
15.如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,B E的垂直平分线交BC的延长线于点F,连结EF交CD于点G,若G是CD的中点,则BC的长是_________.
E的垂直平分线交BC的延长线于点F,连结EF交CD于点G,若G是CD的中点,则BC的长是_________.
16.如图2是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC, 且∠AOB=120°,折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切, 且AO∥GH.
且AO∥GH.
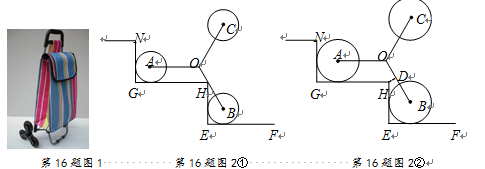
(1)如图2①,若点H在线段OB上,则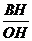 的值是_________.
的值是_________.
(2)如果一级楼梯的高度HE=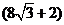 cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 _________.
cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 _________.
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.计算: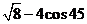 °
°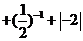 .
.
18.先化简,再求值: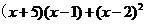 ,其中
,其中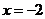 .
.
19.在棋盘中建立如图所示的直角坐标系,三颗棋子A,O,B的位置如图,它们的坐标分别是(-1,1),(0,0)和(1,0).
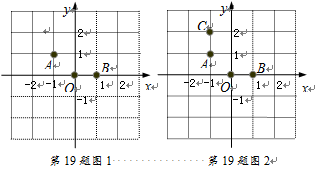
(1)如图2,添加棋子C,使A,O,B, C四颗棋子成为一个轴对称图形,请在图 中画出该图形的对称轴.
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
20.九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如下统计图.
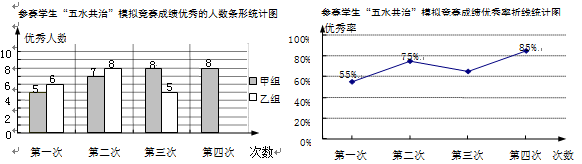
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整.
(2)已求得甲组成绩优秀人数的平均数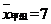 ,方差
,方差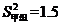 ,请通过计算说明,哪一组成绩优秀的人数较稳定?
,请通过计算说明,哪一组成绩优秀的人数较稳定?
21.受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,义乌市某服装厂每件衣服原材料的成本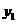 (元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本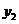 (元)与月份x的函数关系式为
(元)与月份x的函数关系式为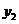 =x+62(8≤x≤12,且x为整数).
=x+62(8≤x≤12,且x为整数).
(1) 请观察表格中的数据,用学过的函数相关知识求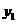 与x的函数关系式.
与x的函数关系式.
(2) 若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量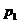 (万件)与月份x满足关系式
(万件)与月份x满足关系式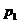 =0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量
=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量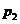 (万件)与月份x满足关系式
(万件)与月份x满足关系式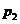 =
= -0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大?并求出最大利润.
-0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大?并求出最大利润.
22.
(1)阅读合作学习内容,请解答其中的问题.
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
23.等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.
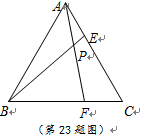
(1)若AE=CF.
①求证:AF=BE,并求∠APB的度数.
②若AE=2,试求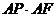 的值.
的值.
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
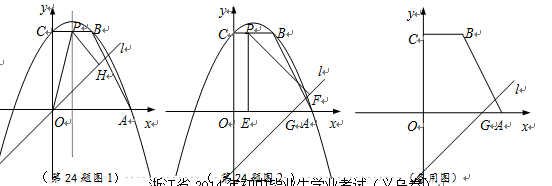
24.如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.
(1)求该抛物线的函数解析式.
(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积.
 ②当m=-3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由
②当m=-3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由
浙江省2014年初中毕业生学业考试(义乌卷)
数学试卷参考答案及评分标准
一、 选择题(本题有10小题,每小题3分,共30分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | A | D | D | C | C | C | B | D | A |
评分标准 | 选对一题给3分,不选,多选,错选均不给分 | |||||||||
二、填空题 (本题有6小题,每小题4分,共24分)
11.如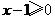 等 12.x=2 13.80 14.
等 12.x=2 13.80 14.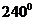 15.7
15.7
16.(1)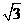 (2分);(2)
(2分);(2)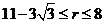 (2分)
(2分)
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.原式=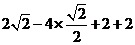 ……4分
……4分
=4 ……2分
18.原式=x2-x+5x-5+x2-4x+4=2x2-1,……4分
当x=-2时,原式=2×(―2)2―1=7. ……2分
19.(1)如图. ……2分
(2)(-1,-1), (0,-1), (2,1) (写出2个即可).
……4分
20.(1)抽取的学生数为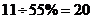 ,
,
∴第三次成绩的优秀率为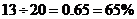 . ……2分
. ……2分
第四次成绩优秀的人数为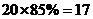 ,乙组成绩优秀的人数
,乙组成绩优秀的人数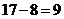 ,
,
补充后的条形统计图如下图所示: ……2分
(2)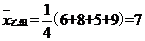 ,
,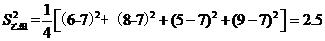 ,
,
因为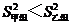 ,所以甲组成绩优秀的人数较稳定. ……4分
,所以甲组成绩优秀的人数较稳定. ……4分
21. (1) 由表格中数据可猜测,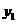 是x的一次函数.
是x的一次函数.
设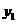 =
=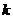 x+b 则
x+b 则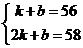 解得:
解得: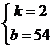
∴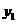 =2x+54,
=2x+54,
经检验其它各点都符合该解析式,
∴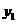 =2x+54(1≤x≤7,且x为整数). ……3分
=2x+54(1≤x≤7,且x为整数). ……3分
(2)设去年第x月的利润为 万元.
万元.
当1≤x≤7,且x为整数时,
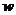 =
=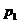 (100-8-
(100-8-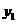 )=(0.1x+1.1)(92-2x-54)= -0.2
)=(0.1x+1.1)(92-2x-54)= -0.2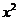 +1.6x+41.8
+1.6x+41.8
=-0.2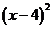 +45,
+45,
∴当x=4时,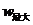 =45万元; ……2分
=45万元; ……2分
当8≤x≤12,且x为整数时,
 =
=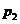 (100-8-
(100-8-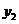 )=(-0.1x+3)(92-x-62)=0.1
)=(-0.1x+3)(92-x-62)=0.1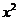 -6x+90
-6x+90
=0.1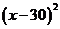 ,
,
∴当x =8时,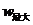 =48.4万元. ……2分
=48.4万元. ……2分
∴该厂去年8月利润最大,最大利润为48.4万元. ……1分
22.(1)①∵OD=3,DE=2,∴E(2,3),由反比例函数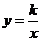 ,可得k=xy=6,
,可得k=xy=6,
∴该反比例函数的解析式是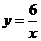 . ……2分
. ……2分
②设正方形AEGF的边长为a,则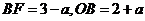 ,
,
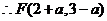 ,
,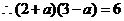 ,
,
解得a1=0(舍去),a2=1,
∴点F的坐标为(3,2). ……3分
(2)两个矩形不可能全等. ……2分
当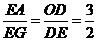 时,两个矩形相似,
时,两个矩形相似,
方法1: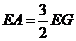 ,设
,设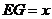 ,则
,则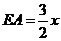 ,
,
∴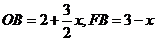 ,∴
,∴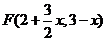 ,
,
∴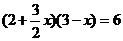 ,解得
,解得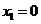 (舍去),
(舍去),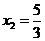 ,∴
,∴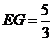 ,
,
∴矩形AEGF与矩形DOHE的相似比为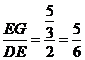 .
.
方法2:设 矩形AEGF与矩形DOHE的相似比为t.则
矩形AEGF与矩形DOHE的相似比为t.则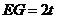 ,
,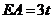 ,
,
∴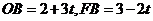 ,∴
,∴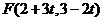 ,
,
∴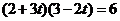 ,解得
,解得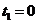 (舍去),
(舍去),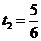 ,
,
∴矩形AEGF与矩形DOHE的相似比为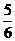 . ……3分
. ……3分
23.(1)①如图,∵△ABC是等边三角形,
∴∠C=∠BAC=60°, AB=AC,
又∵AE=CF,
∴△AFC≌△BEA (SAS),
∴AE=CF, ……2分
∠1=∠3,
∵∠4=∠2+∠3,
∴∠4=∠2+∠1=∠BAC=60°,
即∠ APB=180°-∠4=120°. ……2分
APB=180°-∠4=120°. ……2分
② ∵ ∠C=∠4=60°,∠PAE=∠CAF,
∴ △APE∽△ACF,
∴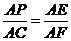 ,即
,即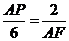 ,所以
,所以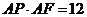 . ……2分
. ……2分
(2)若AF=BE,有AE=BF或AE=CF两种情况.
当AE=BF时,如图2,此时点P经过的路径是AB边上的高线CH.
在Rt△AHC中,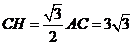 ,
,
∴此时点P经过的路径长为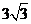
 .
.
当AE=CF时,如图3,点P经过的路径是以A,B为端点的 圆弧,且∠APB=120°,则圆心角∠AOB=120°,
过点O作OG⊥AB, 在Rt△AOG中,∠AOG=60°,
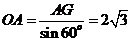 ,
,
∴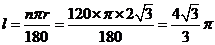 .
.
∴此时点P经过的路径长为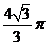 .
.
所以,点P经过的路径长为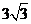 或
或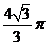 . ……4分
. ……4分
24.(1)设抛物线的解析式为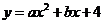 ,由对称轴x=1,可得点B坐标(2,4),
,由对称轴x=1,可得点B坐标(2,4),
∴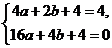 解得
解得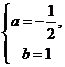 ∴
∴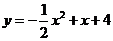 . ……4分
. ……4分
(2)①PH⊥直线l,有ON=MN=1,PM=3,
由△PMH为等腰直角三角形得HM=PH=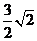 ,
,
所以,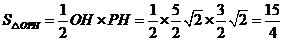 . ……4分
. ……4分


