(单词翻译:单击)
一、选择题(本题共12小题,每小题选对得3分,选错、不选或选出的答案超过一个均记零分,共36分)
1.下列四个 实数中,是无理
实数中,是无理 数的为( )
数的为( )
A. 0 B. -3 C.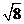 D.
D.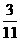

2.下面计算正确的是( )
A. 3a-2a=1 B. 3a2+2a=5a3 C. (2ab)3=6a3b3 D. -a4•a4=-a8

【考点】1.幂的乘方与积的乘方;2.合并同类项;3.同底数幂的乘法.
3.2014年4月25日青岛世界园艺博览会成功开幕,预计将接待1500万人前来观赏,将1500万用科学记数法表示为( )
A. 15×105 B. 1.5×106 C. 1.5×107 D. 0.15×108
【答案】C.
【解析】
试题分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把
4.如图是由4个相同的小正方形搭成的一个几何体,则它的俯视图是( )
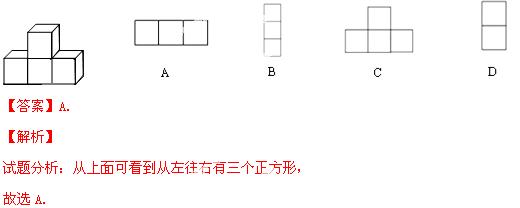
【考点】简单组合体的三视图.
5.对参 加某次野外训练的中学生的年龄(单位:岁)进行统计,结果如表:
加某次野外训练的中学生的年龄(单位:岁)进行统计,结果如表:
年龄 | 13 | 14 | 15 | 16 | 17 | 18 |
人数 | 4 | 5 | 6 | 6 | 7 | 2 |
 则这些学生年龄的众数和中位数分别是( )
则这些学生年龄的众数和中位数分别是( )
A. 17,15.5 B. 17,16 C. 15,15.5  D. 16,16
D. 16,16

6.若一个正n边形的每个内角为156°,则这个正n边形的边数是( )
)
A. 13 B. 14 C. 15 D. 1 6
【答案】C.
【解析】
试题分析:∵一个正多边形的每个内角都为156°,
∴这个正多边形的每个外角都为:180°-156°=24°,
∴这个多边形的边数为:360°÷24°=15,
故选C.
【考点】多边形内角与外角.
7.已知A、C两地相距40千米,B、C两地相距50千米,甲 乙两车分别从A、B两地同时出发到C地.若乙车每小时比甲车多行驶12千米,则两车同时到达C地.设乙车的速度为x千米/小时,依题意列方程正确的是( )
乙两车分别从A、B两地同时出发到C地.若乙车每小时比甲车多行驶12千米,则两车同时到达C地.设乙车的速度为x千米/小时,依题意列方程正确的是( )
A. 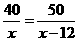 B.
B.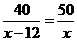 C.
C.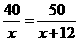 D.
D. 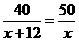

8.如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
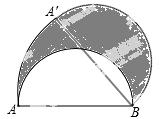
A. π B. 2π C.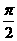 D. 4π
D. 4π

9.一个圆锥的侧面展开图是半径为R的半圆,则该圆锥的高是( )
A. R B.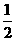 R C.
R C.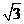 R D.
R D. 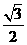 R
R

【考点】圆锥的计算.
10.如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=(  )
)
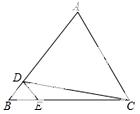
A. 1:16 B. 1:18 C. 1:20 D. 1:24

∴S△BDE:S△ACD=a:20a=1:20.
故选C.
【考点】相似三角形的判定与性质.
11.如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是( )
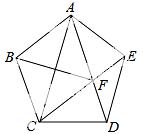
A.△CDF的周长等于AD+CD B.FC平分∠BFD C.AC2+BF2=4CD2 D. DE2=EF•CE
【答案】
【解析】

∴AC2+BF2=4CD2.
故C说法正确;
由正五边形的性质得,△ADE≌△CDE,
∴∠DCE=∠EDF,
∴△CDE∽△DFE,
∴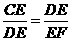 ,
,
∴DE2=EF•CE,
故C说法正确;
故选B.
【考点】正多 边形和圆.
边形和圆.
12.已知二次函数y=ax2+bx+c的图象如图所示.下列结论:
①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2
其中正确的个数有( )
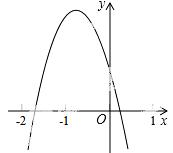
A. 1 B. 2 C. 3 D. 4
【答案】D.
【解析】

∵当x=-1时,y>0,
∴a-b+c>0,
∵当x=1时,y<0,
∴a+b+c<0,
∴(a-b+c)(a+b+c)<0,即(a+c-b)(a+c+b)<0,
∴(a+c)2-b 2<0,所以④正确.
2<0,所以④正确.
故选D.
【考点】二次函数图象与系数的关系.
二、填空题(本题包括5小题,每小题4分,共20分)
13.分解因式:a3-4ab2=
【答案】a(a+2b)(a-2b).
【解析】

【考点】1.实数的运算;2.零指数幂;3.负整数指数幂.
15.若关于x的方程x2+(k-2)x+k2=0的两根互为倒数,则k=
【答案】-1.
【解析】
试题分析:根据已知和根与系数的关系x1x2=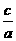 得出k2=1,求出k的值,再根据原方程有两个实数根,求出符合题意的k的值.
得出k2=1,求出k的值,再根据原方程有两个实数根,求出符合题意的k的值.
试题解析:∵x1x2=k2,两根互为倒数,
∴k2=1,
解得k=1或-1;
∵方程有两个实数根,△>0,
∴当k=1时,△<0,舍去,
故k的值为-1.
【考点】根与系数的关系.
16.已知一次函数y=ax+b与反比例函数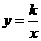 的图象相交于A(4,2)、B(-2,m)两点,则一次函数的表达式为
的图象相交于A(4,2)、B(-2,m)两点,则一次函数的表达式为

【考点】反比例函数与一次函数的交点问题.
17.如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为 .
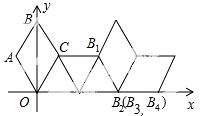
【答案】(1342,0).
【解析】
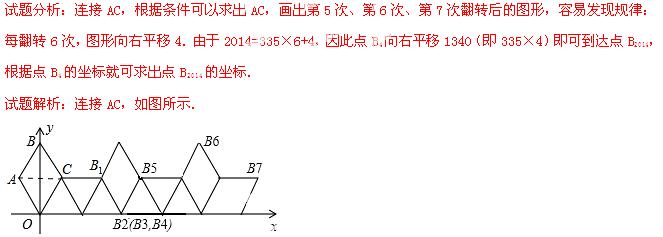
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=90°,
∴△ABC是等边三角形.
∴AC=AB.
∴AC=OA.
∵OA=1,
∴AC=1.

【考点】1.规律型:点的坐标;2.等边三角形的判定与性质;3.菱形的性质.
三、解答题(本大题共7小题,共64分,解答要写出必要的文字说明,证明过程或推演步骤)
18.先化简,再求值: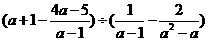 ,其中a=-1.
,其中a=-1.

【考 点】分式的化简求值.
点】分式的化简求值.
19.在某市开展的“读中华经典,做书香少年”读书月 活动中,围绕学生日人均阅读时间这一问题,对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题:
活动中,围绕学生日人均阅读时间这一问题,对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题:
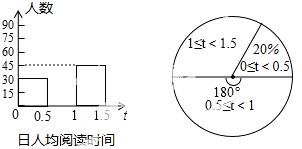
(1)本次抽样调查的样本容量是多少?
(2)请将条形统计图补充完整.
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角度数.
(4)根据本次抽样调查,试估计该市12000名初二学生中日人均阅读时间在0.5~1.5小时的多少人.
【答案】(1) 150;(2)补图见解析;(3)108°;(4)6000.
【解析】
试题分析:(1)根据第一组的人数是30,占20%,即可求得总数,即样本容量;
(2)利用总数减去另外两段的人数,即可求得0.5~1小时的人数,从而作出直方图;
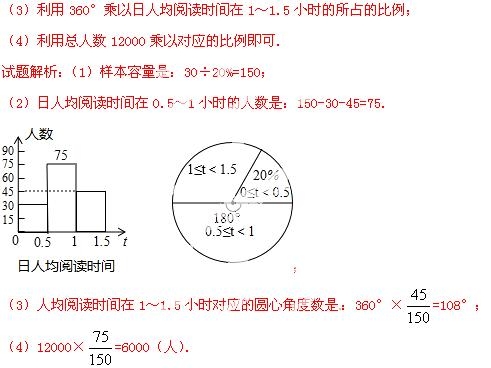
【考点】1.条形统计图;2.用样本估计总体;3.扇形统计图.
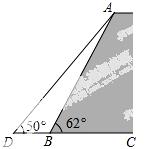
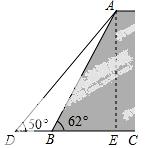
20.如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡 面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)
面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)
(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
【答案】6.58米.
【解析】
试题分析:过A点作AE⊥CD于E.在Rt△ABE中,根据三角函数可得AE,BE,在Rt△ADE中,根据三角函数可得DE,再根据DB=DC-BE即可求解.
试题解析:过A点作AE⊥CD于E.

【考点】解直角三角形的应用-坡度坡角问题.
21.如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.
(1)求证:BE=CD;
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明.
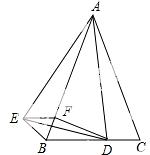

∴AB=AC,
∴∠BAE=∠CAD,
在△ACD和△ABE中,
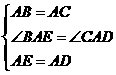 ,
,
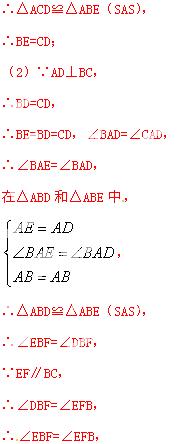
∴EB=EF,
∴BD=BE=EF=FD,
∴四边形BDFE为菱形.
【考点】1.全等三角形的判定与性 质;2.菱形的判定;3.旋转的性质.
质;2.菱形的判定;3.旋转的性质.
22.某市为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工 程、已知2013年投资1000万元,预计2015年投资1210万元.若这两年内平均每年投资增长的百分率相同.
程、已知2013年投资1000万元,预计2015年投资1210万元.若这两年内平均每年投资增长的百分率相同.
(1)求平均每年投资增长的百分率;
(2)已知河道治污每平方需投入400元,园林绿化每平方米需投入200元,若要求2015年河道治污及园林绿化总面积不少于35000平方米,且河道治污费用不少于园林绿化费用的4倍,那么园林 绿化的费用应在什么范围内?
绿化的费用应在什么范围内?
【答案】(1)10%;(2)园林绿化的费用应在190万~242万的范围内.
【解析】

由题意,得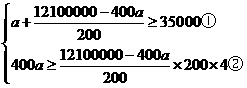 ,
,
由①得a≤25500,
由②得a≥24200,
∴24200≤a≤25500,
∴968万≤400a≤1020万,
∴190万≤1210万-400a≤242万,
答:园林绿化的费用应在190万~242万的范围内.
【考点】1.一元二次方程的应用;2.一元一次不等式组的应用.
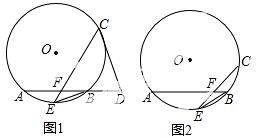
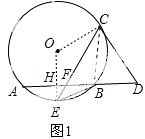
23.如图1,在⊙O中,E是弧AB的中点,C为⊙O上的一动点(C与E在AB异侧),连接EC交AB于点F,EB=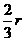 (r是⊙O的半径).
(r是⊙O的半径).
(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切;
(2)求EF•EC的值;
(3)如图2,当F是AB的四等分点时,求EC的值.
【答案】(1)证明见解析;(2)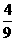 r2;(3)
r2;(3)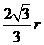 .
.
【解析】
 AB的四等分点,所以HF=
AB的四等分点,所以HF=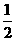 AH=
AH=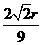 ,于是在Rt△EFH中可计算出EF=
,于是在Rt△EFH中可计算出EF=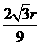 ,然后利用(2)中的结论可计算出EC.
,然后利用(2)中的结论可计算出EC.
试题解析:(1)证明:连结OC、OE,OE交AB于H,如图1,
∵E是弧AB的中点,
∴OE⊥AB,
∴∠EHF=90°,
∴∠HEF+∠HFE=90°,
而∠HFE =∠CFD,
=∠CFD,
∴∠HEF+∠CFD=90°,
∵DC=DF,
∴∠CFD=∠DCF,
而OC=OE,
∴∠OCE=∠OEC,
∴∠OCE+∠DCE=∠HEF+∠CFD=90°,
∴OC⊥CD,
∴直线DC与⊙O相切;
(2)解:连结BC,
∵E是 的中点,
的中点,
∴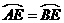 ,
,
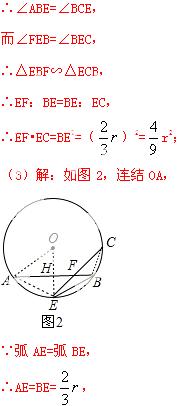
设OH=x,则HE=r-x,
在Rt△OAH中,AH2+OH2=OA2,即AH2+x2=r2,
在Rt△EAH中,AH2+EH2=EA2,即AH2+(r-x)2=(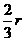 )2,
)2,
∴x2-(r-x)2=r2-(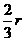 )2,即得x=
)2,即得x=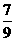 r,
r,
∴HE=r-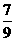 r=
r=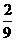 r,
r,

【考点】圆的综合题.
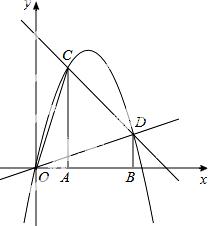
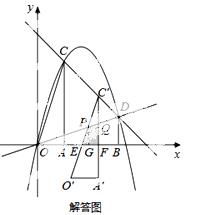
24.如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.
(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.
【答案】(1)y=-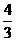 x2+
x2+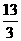 x.(2)
x.(2)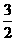 或
或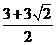 或
或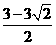 .(3)
.(3)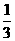 .
.
【解析】
试题分析:(1)利用待定系数法求出抛物线的 解析式;
解析式;
(2)由题意,可知MN∥AC,因为以A、C、M、N为顶点的四边形为平行四边形,则有MN=AC=3.设点M的横坐标为x,则求出MN=|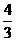 x2-4x|;解方程|
x2-4x|;解方程|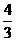 x2-4x|=3,求出x的值,即点M横坐标的值;
x2-4x|=3,求出x的值,即点M横坐标的值;
(3)设水平方向的平移距离为t(0≤t<2),利用平移性质求出S的表达式:S=-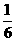 (t-1)2+
(t-1)2+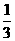 ;当t=1
;当t=1

由题意,可知MN∥AC, 因为以A、C、M、N为顶点的四边形为平行四边形,则有MN=AC=3.
因为以A、C、M、N为顶点的四边形为平行四边形,则有MN=AC=3.
∴|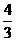 x2-4x|=3.
x2-4x|=3.
若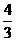 x2-4x=3,整理得:4x2-12x-9=0,解得:x=
x2-4x=3,整理得:4x2-12x-9=0,解得:x=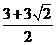 或x=
或x=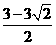 ;
;

∴直线O′C′的解析式为y=3x-4t.
∴E(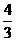 t,0).
t,0).
联立y=3x-4t与y=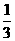 x,解得x=
x,解得x=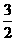 t,∴P(
t,∴P(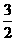 t,
t,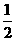 t).
t).
过点P作PG⊥x轴于点G,则PG=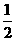 t.
t.
∴S=S△OFQ-S△OEP=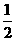 OF•FQ-
OF•FQ-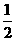 OE•PG
OE•PG
=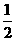 (1+t)(
(1+t)(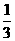 +
+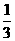 t)-
t)-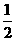 •
•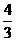 t•
t•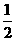 t
t
=-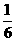 (t-1)2+
(t-1)2+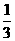
当t=1时,S有最大值为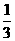 .
.
∴S的最大值为 .
.
【考点】二次函数综合题.


