(单词翻译:单击)
一、选择题(本大题共有12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合题目要 求.)
求.)
1.在下列平面图形中,既是轴对称图形又是中心对称图形的是( )


【考点】1.中心对称图 形;2.轴对称图形.
形;2.轴对称图形.
2.去年我市参 加中考
加中考 人数约17700人,这个数用科学记数法表示是( )
人数约17700人,这个数用科学记数法表示是( )
A. 1.77×102 B. 1.77×104 C. 17.7×103 D. 1.77×105

【考点】科学记数法—表示较大的数.
3.如果一个多边形的内角和是720°,那么这个多边形是( )
A. 四边形 B. 五边形 C. 六边形 D. 七边形
【答案】C.
【解析】
试题分析:设这个正多边形的边数是n,则
(n﹣2)•180° =720°,
=720°,
解 得:n=6.
得:n=6.
则这个正多边形的边数是6.
故选C.
【考点】多边形内角与外角.
4.数据5,8,4,5,3的众数和平均数分别是( )
A. 8,5 B. 5,4 C. 5,5 D. 4,5

【考点】1.众数;2.算术平均数.
5.下列运算正确的是( )
A.(﹣a3)2=a5 B.(﹣a3)2=﹣a5 C.(﹣3a2)2=6a4 D.(﹣3a2)2=9a4
D.(﹣3a2)2=9a4

【考点】幂的乘方与积的乘方.
6.正方形的一条对角线长为4,则这个正方形的面积是( )
A. 8 B. 4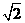 C. 8
C. 8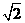 D. 16
D. 16
【答案】A.
【解析】
试题分析:∵正方形的一条对角线长为4,
∴这个正方形的面积=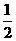 ×4×4=8.
×4×4=8.
故选A.
【考 点】正方形的性质.
点】正方形的性质.
7.函数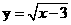 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A. x≠3 B. x≥3 C. x>3 D. x≤3

8.将分式方程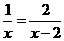 去分母后得到的整式方程,正确的是( )
去分母后得到的整式方程,正确的是( )
A. x﹣2=2x B. x2﹣2x=2x C. x﹣2=x D. x= 2x﹣4
2x﹣4

9.顺次连接菱形各边的中点所形成的四边形是( )
A. 等腰梯形 B. 矩形 C. 菱形 D. 正方形

故选B.
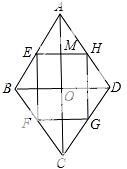
【考点】1.正方形的判定;2.三角形中位线定理;3.菱形的性质.
10.已知一元二次方程的两根分别是2和﹣3,则这个一元二次方程是( )
A. x2﹣6x+8=0 B. x2+2x﹣3=0 C. x2﹣x﹣6=0 D. x2+x﹣6=0

11.不等式组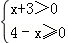 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
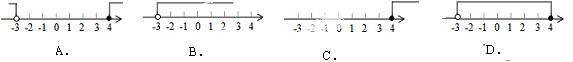
【答案】D.
【解析】
试题分析:解得﹣3<x≤4,
故选D.
【考点】1.解一元一次不等式组;2.在数轴上表示不等式的解集.
12.将点P(﹣2,3)向右平移3个单位得到点P1,点P2与点 P1关于原点对称,则P2的坐
P1关于原点对称,则P2的坐 标是( )
标是( )
A. (﹣5,﹣3) B. (1,﹣3) C. (﹣1,﹣3) D. (5,﹣3)

【考点】1.关于原点对称的点的坐标;2.坐标与图形变化-平移.
二、填空题:本大题共6小题,每小题3分,共18分
13.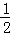 的倒数是 .
的倒数是 .

【考点】因式分解-运用公式法.
15.一 个圆柱的底面直径为6cm,高为10cm,则这个圆柱的侧面积是 cm2(结果保留π).
个圆柱的底面直径为6cm,高为10cm,则这个圆柱的侧面积是 cm2(结果保留π).
【答案】60π.
【解析】
试题分析:直接利用圆柱体侧面积公式求出即可.
试题解析:∵一个圆柱的底面直径为6cm,高为10cm,
∴这个圆柱的侧面积是:πd×10=60π(cm2).
【考点】几何体的表面积.
16.某校在九年级的一次模拟考试中,随机抽取40名学生的数学成绩进行分析,其中有10名学生的成绩达1 08分以上,据此估计该校九年级640名学生中这
08分以上,据此估计该校九年级640名学生中这 次模拟考数学成绩达108分以上的约有 名学生.
次模拟考数学成绩达108分以上的约有 名学生.

【考点】用样本估计总体.
17.如图,Rt△ABC中,∠C=90°,∠B=30°,BC=6,则AB的长为 .
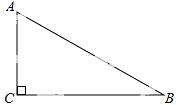

【考点】解直角三角形.
18.如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB= 度.
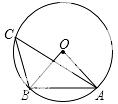
【答案】40.
【解析】
试题分析:由∠C=50°求出∠AOB的度数,再根据等腰三角形的性质和三角形的内角和定理,即可求得答案.
试题解析:∵∠C=50°,
∴∠AOB=2∠C=100°,
∵OA=OB,
∴∠OAB=∠OBA=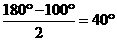 .
.
【考点】圆周角定理.
三、解答题:本大题共7小题,满分66分,解答应写出文字说明、证明过程或演算步骤.
19.(1)计算:(﹣1)2014﹣|﹣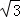 |+
|+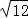 ﹣(
﹣(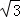 ﹣π)0;
﹣π)0;
(2)先化简,再求值
 :(2x﹣1)2﹣2(3﹣2x),其中x=﹣2.
:(2x﹣1)2﹣2(3﹣2x),其中x=﹣2.

【考点】1.实数的运算;2.整式的混 合运算—化简求值;3
合运算—化简求值;3 .零指数幂.
.零指数幂.
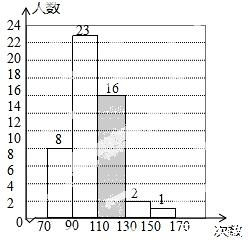
20.某校为了了解学生大课间活动的跳绳情况,随机抽取了50名学生每分钟跳绳的次数进行统计,把统计结果绘制成如表和直方图.
次数 | 70<x<90 | 9 | 110≤x<13 | 130≤x<150 | 150≤x<170 |
人数 | 8 | 23 | 16 | 2 | 1 |
根据所给信息,回答下列问题:
(1)本次调查的样本容量是 ;
(2)本次调查中每分钟跳绳次数达到110次以上(含110次)的共有的共有 19 人;
(3)根据上表的数据补全直方图;
(4)如果跳绳次数达到130次以上的3人中有2名女生和一名男生,学校从这3人中抽取2名学生进行经验交流,求恰好抽中一男一女的概率(要求用列表法或 树状图写出分析过程).
树状图写出分析过程).

【答案】(1)50; (2)19;(3)补图见解析;(4)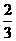 .
.
【解析】

(4) 根据题意画树状图如下:
根据题意画树状图如下:
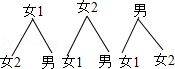
共有6种情况,恰好抽中一男一女的有4种情况,
则恰好抽中一男一女的概率是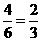 .
.
【考点】1.频数(率)分布直方图;2.频数(率)分布表;3.列表法与树状图法.
21.如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O.(要求用尺规左图,保留作图痕迹,不要求写作法);
(2)求证:DE=BF.
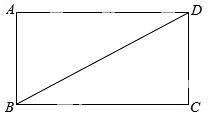
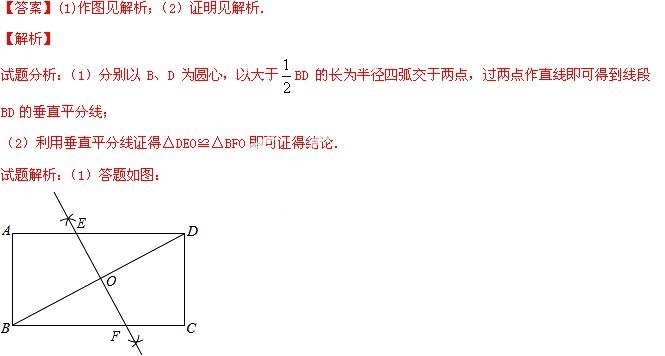
(2)∵四边形ABCD为矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵EF垂直平分线段BD,
∴BO=DO,
在△DEO和三角形BFO中,
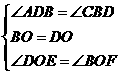 ,
,
∴△DEO≌△BFO(ASA),
∴DE=BF.
【考点】1.作图—基本作图;2.线段垂直平分线的性质;3.矩形的性质.
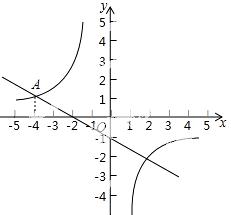
22.一次函数y1=﹣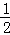 x﹣1与反比例函数y2=
x﹣1与反比例函数y2=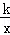 的图象交于点A(﹣4,m).
的图象交于点A(﹣4,m).
(1)观察图象,在y轴的左侧,当y1>y2时,请直接写出x的取值范围;
(2)求出反比例函数的解析式.
【答案】(1)x<﹣4;(2)y2=﹣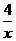 .
.
【解析】

【考点】反比例 函数与一次函数的交点问题.
函数与一次函数的交点问题.
23.甲、乙两个厂家生产的办公桌和办公椅的质量、价格一致,每张办公桌800元,每张椅子80元.甲、乙两个厂家推出各自销售的优惠方案,甲厂家:买一张桌子送三张椅子;乙厂家:桌子和椅子全部按原价8折优惠.现某公司要购买3张办公桌和若干张椅子,若购买的椅子数为x张(x≥9).
(1)分别用含x的式子表示甲、乙两个厂家购买桌椅所需的金额;
 (2)购买的椅子至少多少张时,到乙厂家购买更划算?
(2)购买的椅子至少多少张时,到乙厂家购买更划算?

【考点】一元一次不等式的应用.
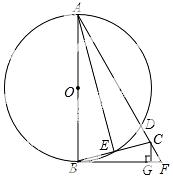
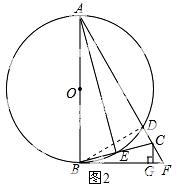
24.如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O于点E,且∠BAF=2∠CBF,CG⊥BF于点G,连接AE.
(1)直接写出AE与BC的位置关系;
(2)求证:△BCG∽△ACE;
(3)若∠F=60°,GF=1,求⊙O的半径长.
【答案】(1) AE⊥BC.(2)证明见解析;(3)2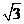 +3.
+3.
【解析】

∴AE⊥BC.
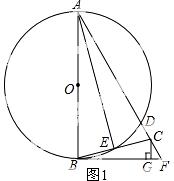
(2)如图1,
∵BF与⊙O相切,
∴∠ABF=90°.
∴∠CBF=90°﹣∠ABE=∠BAE.
∵∠BAF=2∠CBF.
∴ ∠BAF=2∠BAE.
∠BAF=2∠BAE.
∴∠BAE=∠CAE.
∴∠CBF=∠CAE.
∵ CG⊥BF,AE⊥BC,
CG⊥BF,AE⊥BC,
∴∠CGB=∠AEC=90°.
∵∠CBF=∠CAE,∠CGB=∠AEC,
∴△BCG∽△ACE.

∵CG=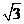 ,
,
∴CD=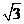 .
.
∵∠AFB=60°,∠ABF=90°,
∴∠BAF=30°.
∵∠ADB=90°,∠BAF=30°,
∴AB=2BD.
∵∠BAE=∠CAE,∠AEB=∠AEC,
∴∠ABE=∠ACE.
∴AB=AC.
设⊙O的半径为r,则AC=AB=2r,BD=r.
∵∠ADB=90°,
∴AD=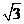 r.
r.
∴DC=AC﹣AD=2r﹣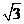 r=(2﹣
r=(2﹣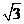 )r=
)r=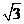 .
.
∴r=2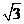 +3.
+3.
∴⊙O的半径长为2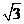 +3.
+3.
【考点 】圆的综合题.
】圆的综合题.
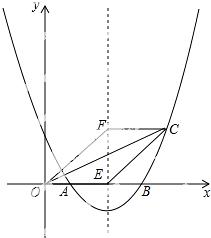
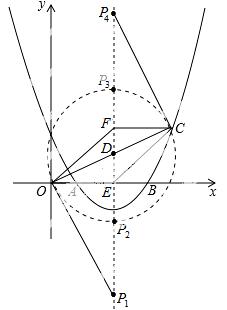
25.如图,抛物线y=ax2 +bx+2与x轴交于点A(1,0)和B(4,0).
+bx+2与x轴交于点A(1,0)和B(4,0).
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且 四边形OECF是平行四边形,求点C的坐
四边形OECF是平行四边形,求点C的坐 标;
标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点 P的坐标;若不存在,请说明理由.
P的坐标;若不存在,请说明理由.
 △PEO相似,根据相似三角形对应边成比例求出PE,然后写出点P的坐标即可;②点C是直角顶点时,同理求出PF,再求出PE,然后写出点P的坐标即可;③点P是直角顶点时,利用勾股定理列式求出OC,然后根据直角三角形斜边上的中线等于斜边的一半可得PD=
△PEO相似,根据相似三角形对应边成比例求出PE,然后写出点P的坐标即可;②点C是直角顶点时,同理求出PF,再求出PE,然后写出点P的坐标即可;③点P是直角顶点时,利用勾股定理列式求出OC,然后根据直角三角形斜边上的中线等于斜边的一半可得PD=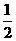 OC,再分点P在OC的上方与下方两种情况写出点P的坐标即可.
OC,再分点P在OC的上方与下方两种情况写出点P的坐标即可.
试题解析:(1)把点A(1,0)和B(4,0)代入y=ax2+bx+2得,
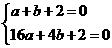 ,
,

∴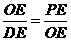 ,
,
即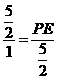 ,
,
解得PE=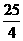 ,
,

【考点】二次函数综合题.


