(单词翻译:单击)
A卷(共100分)
第I卷(选择题,共30分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
1.在-2,-1、0、2这四个数中,最大的数是( )
(A)-2 (B)-1 (C)0 (D)2
2.下列几何体的主视图是三角形的是( )

(A) (B) (C) (D)
3.正在建设的成都第二绕城高速全长超过220公里,串起我市二、三圈层以及周边的广汉、简阳等地,总投资达290亿元,用科学计数法表示290亿元应为( )
(A)290×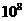 (B)290×
(B)290×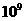
(C)2.90× (D)2.90×
(D)2.90×
4.下列计算正确的是( )
(A) (B)
(B)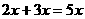
(C)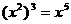 (D)
(D)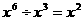
5.下列图形中,不是轴对称图形的是( )
(A) (B) (C) (D)
6.函数 中自变量
中自变量 的取值范围是( )
的取值范围是( )
(A)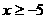 (B)
(B)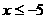 (C)
(C)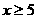 (D)
(D)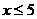
7.如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为( )
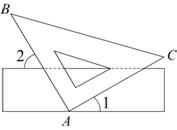
(A)60°
(B)50°
(C)40°
(D)30°
8.近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班的学生成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人 数 | 4 | 8 | 12 | 11 | 5 |
则该办学生成绩的众数和中位数分别是( )
(A)70分,80分 (B)80分,80分
(C)90分,80分 (D)80分,90分
9.将二次函数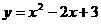 化为
化为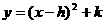 的形式,结果为( )
的形式,结果为( )
(A) (B)
(B)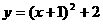
(C)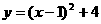 (D)
(D)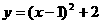
10.在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形AOB的面积是( )
(A)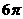
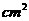 (B)
(B)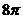
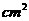 (C)
(C)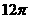
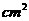 (D)
(D)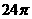
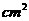
第Ⅱ卷(非选择题,共70分)
二.填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)
11.计算: _______________.
_______________.
12.如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别去OA、OB的中点M,N,测的MN=32 m,则A,B两点间的距离是_____________m.

13.在平面直角坐标系中,已知一次函数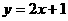 的图像经过
的图像经过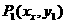 ,
,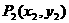 两点,若
两点,若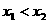 ,则
,则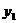 ________
________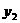 .(填”>”,”<”或”=”)
.(填”>”,”<”或”=”)
14.如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD,若∠ =25°,则∠C =__________度.
=25°,则∠C =__________度.

三.解答题(本大题共6个小题,共54分,解答过程写在答题卡上)
15.(本小题满分12分,每题6分)
(1)计算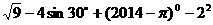 .
.
(2)解不等式组
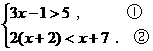
16.(本小题满分6分)
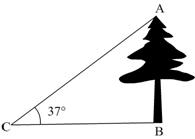
如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,求树的高度AB.
(参考数据: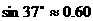 ,
, ,
,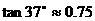 )
)
17.(本小题满分8分)
先化简,再求值: ,其中
,其中 ,
,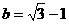 .
.
18.(本小题满分8分)
第十五届中国“西博会”将于2014年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.
(1)若从这20人中随机选取一人作为联络员,求选到女生的概率;
(2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2、3、4、5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.
19.(本小题满分10分)
如图,一次函数 (
(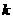 为常数,且
为常数,且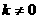 )的图像与反比例函数
)的图像与反比例函数 的图像交于
的图像交于 ,
,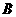 两点.
两点.
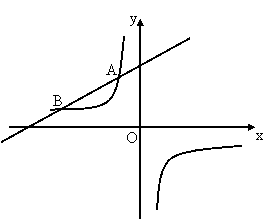
(1)求一次函数的表达式;
(2)若将直线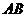 向下平移
向下平移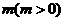 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求 的值.
的值.
20.(本小题满分10分)
如图,矩形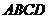 中,
中, ,
,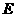 是
是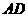 边上一点,
边上一点, (
( 为大于2的整数),连接
为大于2的整数),连接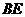 ,作
,作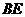 的垂直平分线分别交
的垂直平分线分别交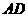 、
、 于点
于点 ,
,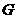 ,
,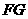 与
与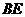 的交点为
的交点为 ,连接
,连接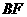 和
和 .
.
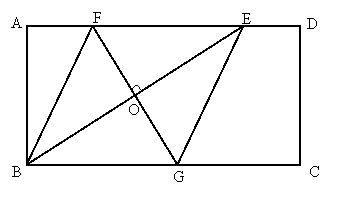
(1)试判断四边形 的形状,并说明理由;
的形状,并说明理由;
(2)当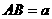 (
( 为常数),
为常数),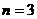 时,求
时,求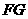 的长;
的长;
(3)记四边形 的面积为
的面积为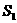 ,矩形
,矩形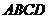 的面积为
的面积为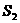 ,当
,当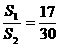 时,求
时,求 的值.(直接写出结果,不必写出解答过程)
的值.(直接写出结果,不必写出解答过程)
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
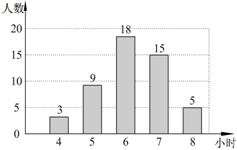
21. 在开展“国学诵读”活动中,某校为了解全校1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据。估计该校1300名学生一周的课外阅读时间不少于7小时的人数是_______.
22. 已知关于 的分式方程
的分式方程 的解为负数,则
的解为负数,则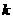 的取值范围是_______.
的取值范围是_______.
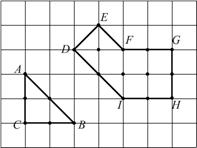
23. 在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如,图中的三角形 是格点三角形,其中S=2,N=0,L=6;图中格点多边形
是格点三角形,其中S=2,N=0,L=6;图中格点多边形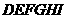 所对应的S,N,L分别是_________.经探究发现,任意格点多边形的面积S可表示为S=aN+bL+c,其中a,b,c为常数,则当N=5,L=14时,S=_________.(用数值作答)
所对应的S,N,L分别是_________.经探究发现,任意格点多边形的面积S可表示为S=aN+bL+c,其中a,b,c为常数,则当N=5,L=14时,S=_________.(用数值作答)
24. 如图,在边长为2的菱形 中,∠
中,∠ =60°,
=60°, 是
是 边的中点,
边的中点,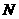 是
是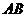 边上一动点,将△
边上一动点,将△ 沿
沿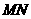 所在的直线翻折得到△
所在的直线翻折得到△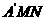 ,连接
,连接 ,则
,则 长度的最小值是_______.
长度的最小值是_______.

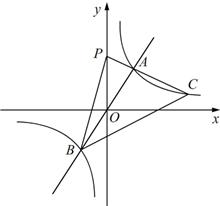
25. 如图,在平面直角坐标系xOy中,直线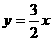 与双曲线
与双曲线 相交于
相交于 ,
,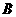 两点,
两点,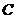 是第一象限内双曲线上一点,连接
是第一象限内双曲线上一点,连接 并延长交
并延长交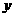 轴于点
轴于点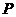 ,连接
,连接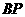 ,
, .若△
.若△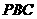 的面积是20,则点
的面积是20,则点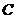 的坐标为___________.
的坐标为___________.
二、解答题(本小题共三个小题,共30分.答案写在答题卡上)
26.(本小题满分8分)
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园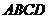 (篱笆只围
(篱笆只围 ,
, 两边),设
两边),设 m.
m.

(1)若花园的面积为192 , 求
, 求 的值;
的值;
(2)若在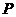 处有一棵树与墙
处有一棵树与墙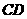 ,
,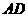 的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积
的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积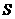 的最大值.
的最大值.
27.(本小题满分10分)
如图,在⊙ 的内接△ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线
的内接△ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线 交⊙O于另一点D,垂足为E.设P是⌒AC上异于A,C的一个动点,射线AP交
交⊙O于另一点D,垂足为E.设P是⌒AC上异于A,C的一个动点,射线AP交 于点F,连接PC与PD,PD交AB于点G.
于点F,连接PC与PD,PD交AB于点G.
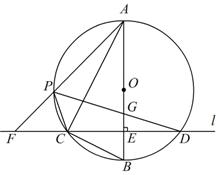
(1)求证:△PAC∽△PDF;
(2)若AB=5,⌒AP=⌒BP,求PD的长;
(3)在点P运动过程中,设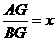 ,
,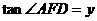 ,求
,求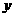 与
与 之间的函数关系式.(不要求写出
之间的函数关系式.(不要求写出 的取值范围)
的取值范围)
28.(本小题满分12分)
如图,已知抛物线 (
(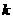 为常数,且
为常数,且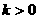 )与
)与 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线 与抛物线的另一交点为D.
与抛物线的另一交点为D.
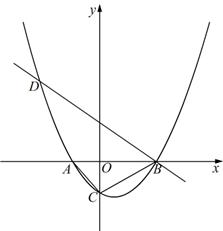
(1)若点D的横坐标为-5,求抛物线的函数表达式;
(2)若在第一象限的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求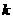 的值;
的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止.当点F的坐标是多少时,点M在整个运动过程中用时最少?
参考答案
A卷
一、选择题
1、D 2、B 3、C 4、B 5、A
6、C 7、A 8、B 9、D 10、C
二、填空题
11、 12、64 13、< 14、40
12、64 13、< 14、40
三、解答题
15、(1)原式=3-2+1-4=-2
(2)由①得x>2,由②x<3
所以,原不等式的解集为2<x<3
16、解:tan37°=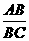 ,所以,AB=0.75×20=15(m)
,所以,AB=0.75×20=15(m)
17、解:原式=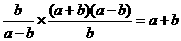 ,
,
当 ,
,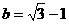 时,原式=2
时,原式=2
18、解:(1)选到女生的概率为:P=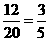
(2)任取2张,所有可能为:23,24,25,34,35,45,共6种,
其中和为偶数的,有:24,35,故甲参加的概率为: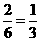 ,而乙参加的概率为:
,而乙参加的概率为: ,
,
所以,游戏不公平。
19、解:(1)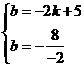 ,解得:b=4,k=
,解得:b=4,k=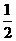 ,
,
所以,一次函数为:y=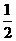 x+5
x+5
(2)向下平移m个单位长度后,直线为: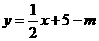 ,
,
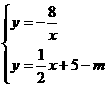 ,化为:
,化为: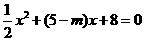 ,
,
Δ=(5-m)2-16=0,解得:m=1或9
20、(1)菱形
因为FG为BE的垂直平分线,所以,FE=FB,GB=GE,∠FEB=∠FBO,
又FE∥BG,所以,∠FEB=∠GBO,所以,∠FBO=∠GBO,BO=BO,∠BOF=∠BOG,
所以,ΔBOF≌ΔBOG,所以,BF=BG,
所以,BG=GE=EF=FB,BFEG为菱形。
(2)AB=a,AD=2a,DE= a,AE=
a,AE=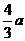 ,BE=
,BE=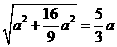 ,OE=
,OE=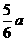 ,
,
设菱形BFEG的边长为x,因为AB2+AF2=BF2,
所以, ,解得:x=
,解得:x=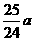 ,所以,OF=
,所以,OF= ,
,
所以,FG=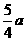
(3)n=6
B卷
一、填空题
21、520
22、K>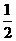 且K≠1
且K≠1
23、7、3、10 11
24、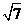 -1
-1
25、
二、解答题
26、(1)12m或16m;(2)195
27、(1)由APCB内接于圆O,得∠FPC=∠B,
又∠B=∠ACE=90°-∠BCE,∠ACE=∠APD,
所以,∠APD=∠FPC,∠APD+∠DPC=∠FPC+∠DPC,即
∠APC=∠FPD,又∠PAC=∠PDC,
所以,△PAC∽△PDF
(2)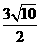
(3)x=2y
28(1)k=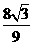
(2)k=
(3)F(-2,2 )
)


