(单词翻译:单击)
一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分)
1. ( 2013云南普洱,1,3分)-2的绝对值是( )
A.2 B.±2 C.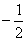 D.
D.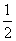
【答案】A
2. ( 2013云南普洱,2,3分)如左下图所示几何体的主视图是( )
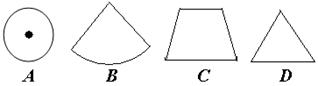
【答案】D
3. ( 2013云南普洱,3,3 分)下列运算正确的是( )
分)下列运算正确的是( )
A.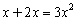 B.
B.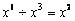 C.
C.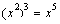 D.
D.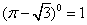
【答案】D
4. ( 2013云南普洱,4,3分)方程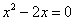 的解为( )
的解为( )
A.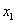 =1,
=1,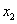 =2 B.
=2 B.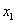 =0,
=0,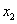 =1 C.
=1 C.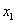 =0,
=0,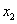 =2 D.
=2 D.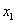 =
=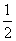 ,
,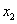 =2
=2
【答案】C
5. ( 2013云南普洱,5,3分)某县一周的最高气温如下表:
星期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期天 |
最高气温(℃) | 32 | 32 | 34 | 30 | 34 | 32 | 29 |
这个县本周每天的最高气温的众数和中位数分别是( )
A.32,32 B.32,34 C.34,34 D.30,32
【答案】A
6. ( 2013云南普洱,6,3分)矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
A.16 B.12 C.24 D.20
【答案】B
7. ( 2013云南普洱,7,3分)如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数是( )
A.40° B. 50° C. 60° D.100°
【答案】B
8. ( 2013云南普洱,8,3分)若ab<0,则正比例函数y=ax和反比例函数y=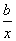 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
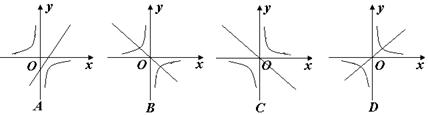
【答案】B
二、填空题(本大题共6个小题,每小题3分,满分18分)
9. ( 2013云南普洱,9,3
( 2013云南普洱,9,3 分)太阳的半径约为696000千米,这个数据用科学记数法表示为
分)太阳的半径约为696000千米,这个数据用科学记数法表示为
千米.
【答案】6.96×105
10. ( 2013云南普洱,10,3分)计算: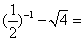 .
.
【答案】0
11. ( 2013云南普洱,11,3分)函数y=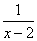 的自变量x的取值范围是 .
的自变量x的取值范围是 .
【答案】x≠2
12. ( 2013云南普洱,12,3分)如图,AB⊥CD,垂足为点B,EF平分∠ABD,则∠CBF的度数为  .
.
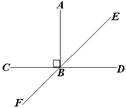
【答案】45°
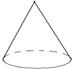
13. ( 2013云南普洱,13,3分)用一个圆心角为150°,半径为2cm的扇形作一个圆锥的侧面,则这个圆锥的底面圆的半径为 cm.
【答案】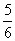
14. ( 2013云南普洱,14,3分)观察下列一组数: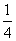 ,
,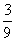 ,
,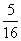 ,
,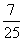 ,
,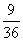 ,…,它们是按一定规律排列的,那么这一组数的第n个数是 .
,…,它们是按一定规律排列的,那么这一组数的第n个数是 .
【答案】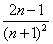
三、解答题(本大题共9个小题,满分58分)
15. ( 2013云南普洱,15,5分)先化简,再求值: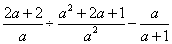 ,其中a=2013.
,其中a=2013.
【答案】解:=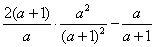 =
=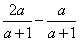
=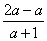 =
=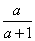
当a=2013,原式=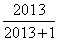 =
=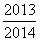 .
.
16. ( 2013云南普洱,16,5分 )解方程:
)解方程: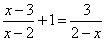
【答案】解:两边同时乘以(x-2),得
x-3+x-2= -3,
解得x=1.
检验:当x=1时,
x-2=1-2= -1≠0,
∴原方程的解为x =1.
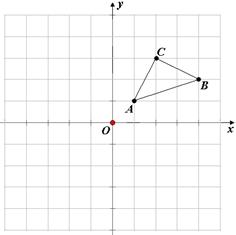
17. ( 2013云南普洱,17,6分)如图,方格纸中的每个小方格都是边长为1个单位的小正方形,每个小正方形 的顶点称为格点.△ABC的顶点都在格点上,建立平面直角坐标系后,点A、B、C的坐标分别为(1,1),(4,2),(2,3).(提示:一定要用2B铅笔作图)
的顶点称为格点.△ABC的顶点都在格点上,建立平面直角坐标系后,点A、B、C的坐标分别为(1,1),(4,2),(2,3).(提示:一定要用2B铅笔作图)
(1)画出△ABC向左平移4个单位,再向上平移1个单位后得到的△A1B1C1;
(2)画出△ABC向关于原点O对称的△A2B2C2;
(3 )以点A、A1、A2为顶点的三角形的面积为 .
)以点A、A1、A2为顶点的三角形的面积为 .
【答案】(1)、(2)答案如图所示:
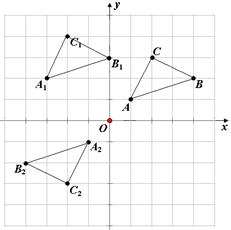
(3)如图所示,
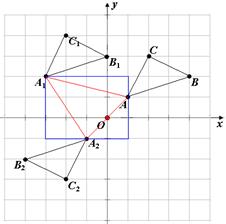
以点A、A1、A2为顶点的三角形的面积为:
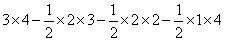 =12-3-2-2=5.
=12-3-2-2=5.
18. ( 2013云南普洱,18,6分)如图,已知点B、E、C、F在同一条直线上,BE=CF,AB∥DE,∠A=∠D.求证:AB=DE.
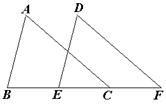
【答案】证明:∵BE=CF,∴BC=EF.
∵AB∥DE,∴∠B=∠DEF.
在△ABC与△DEF中,
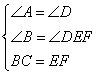 ,
,
∴△ABC≌△DEF(AAS),
∴AB=DE.
19. ( 2013云南普洱,19,7分)我市某中学为了了解本校学生对普洱茶知识的了解程度,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
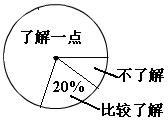
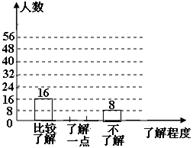
(1)在本次抽样调查中,共抽取了 名学生.
(2)在扇形统计图中,“不了解”部分所对应的圆心角的度数为 .
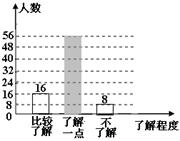
(3)补全条形统计图. (提示:一定要用2B铅笔作图)
(4)若该校有1860名学生,根据调查结果,请估算出对普洱茶知识“了解一点”的学生人数.
【答案】解:(1)80;
(2)36°;
(3)补全条形图如下:
(4)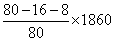 =1302.
=1302.
答:对普洱茶知识“了解一点”的学生人数为1302 .
.
20. ( 2013云南普洱,20,6分)如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两 个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,点Q的坐标记为Q(x,y).
个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,点Q的坐标记为Q(x,y).
(1)用列表法或树状图表示(x,y)所有可能出现的结果;
(2)求出点Q (x,y)落在第四象限的概率.
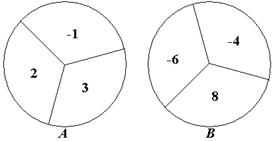
【答案】(1)列表如下:
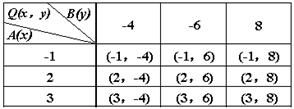
画树状图如下:
(2)由(1)中的表格或树状图可知:
点Q出现的所有可能结果有9种,位于第四象限的结果有2种,
∴点Q (x,y)落在第四象限的概率为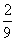 .
.
21. ( 2013云南普洱,21,6分)据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一 条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒.问此车是否超过了该路段16米/秒的限制速度?(参考数据:
条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒.问此车是否超过了该路段16米/秒的限制速度?(参考数据: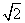 ≈1.4,
≈1.4,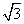 ≈1.7)
≈1.7)
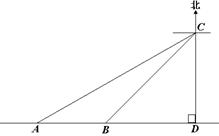
【答案】解:由题意得
在Rt△BCD中,
∵∠BDC=90°,∠BCD=45°,CD=100米,∴BD=CD=100米.
在Rt△ACD中,
∵∠ADC=90°,∠ACD=60°,CD=100米,∴A D=CD·tan∠ACD=100
D=CD·tan∠ACD=100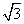 (米).
(米).
∴AB=AD-BD=100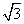 -100≈70(米).
-100≈70(米).
∴此车的速度为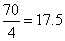 (米/秒).
(米/秒).
∵17.5>16,
∴此车超过了该路段16米/秒的限制速度.
22. ( 2013云南普洱,22,7分)在茶节期间,某茶商订购了甲种茶叶90吨,乙种茶叶80吨,准备用A、B两种型号的货车共20辆运往外地.已知A型货车每辆运费为0.4万元,B型货车每辆运费为0.6万元.
(1)设A型货车安排x辆,总运费为y万元,写出y与x的函数关系式;
(2)若一辆A型货车可装甲种茶叶6吨 ,乙种茶叶2吨;一辆B型货车可装甲种茶叶3吨,乙种茶叶7吨.按此要求安排A、B两种型号货车一次性运完这批茶叶,共有哪几种运输方案?
,乙种茶叶2吨;一辆B型货车可装甲种茶叶3吨,乙种茶叶7吨.按此要求安排A、B两种型号货车一次性运完这批茶叶,共有哪几种运输方案?
(3)说明哪种方案运费最少?最少运费是多少万元?
【答案】解:(1)y=0.4x+0.6(20-x)= -0.2x+12
(2)由题意得
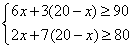 ,
,
解得10≤x≤12.
又∵x为正整数,
∴x=10,11,12,
∴10-x=10,9,8 .
∴有以下三种运输方案:
①A型货车10辆,B型货车10辆;
②A型货车11辆,B型货车9辆;
③A型货车12辆,B型货车8辆.
(3)∵方案①运费:10×0.4+10×0.6=10(万元);
方案②运费:11×0.4+9×0.6=9.8(万元);
方案③运费:12×0.4+8×0.6=9.6(万元).
∴方案③运费最少,最少运费为9.6万元.
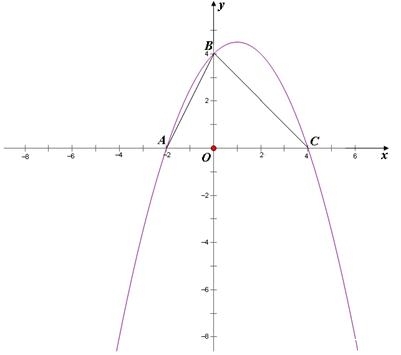
23. ( 2013云南普洱,23,10分)如图,在平面直角坐标系中,抛物线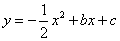 经过A(-2,0),C(4,0)两点,和y轴相交于点B,连接AB、BC.
经过A(-2,0),C(4,0)两点,和y轴相交于点B,连接AB、BC.
(1)求抛物线的解析式(关系式).
(2)在第一象限外,是否存在点E,使得以BC为直角边的△BCE和Rt△AOB相似?若存在,请简要说明如何找到符合条件的点E,然后直接写出点E的坐标,并判断是否有满足条件的点E在抛物线上;若不存在,请说明理由.
(3)在直线BC上方的抛物线上,找一点D,使S△BCD:S△ABC=1:4,并求出此时点D的坐标.
【答案】解:(1)∵抛物线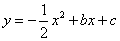 经过A(-2,0),C(4,0)两点,
经过A(-2,0),C(4,0)两点,
∴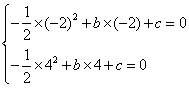 ,解得
,解得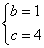 .
.
∴抛物线的解析式为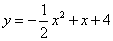 .
.
(2)在第一象限外存在点E,使得以BC为直角边的△BCE和Rt△AOB相似.
①当BC为斜边时,
△BOC即为所找的△BCE是直角三角形,但是它与Rt△AOB不相似;
②当BC为直角边时,
若点B为直角顶点,则点E的坐标为(-8,-4),此时点E不在抛物线上;
若点B为直角顶点,则点E的坐标为(-4,-8),此时点E在抛物线上.
(3)∵S△ABC=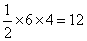 ,S△BCD:S△ABC=1:4,
,S△BCD:S△ABC=1:4,
∴S△BCD=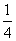 S△ABC =
S△ABC =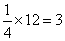 .
.
如图所示,设在直线BC上方的抛物线上,找一点D的坐标为(x,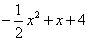 ),作DE⊥x轴于点E,则
),作DE⊥x轴于点E,则
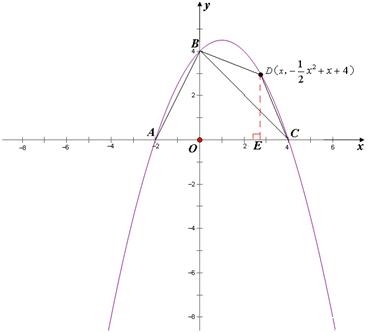
S△BCD=S梯形BOED+S△DCE-S△BOC
=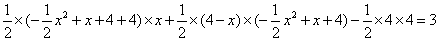 .
.
即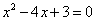 ,
,
解得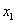
 =1,
=1,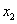 =3.
=3.
∴点D的坐标为(1,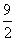 )或(3,
)或(3,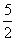 ).
).


