(单词翻译:单击)
一、选择题(共12小题,每小题3分,满分36分。每小题都给出代号为A、B、C、D四个结论,其中只有一个是正确的。)
1.(3分)在实数1、0、﹣1、﹣2中,最小的实数是( )
A.﹣2 B. ﹣1 C. 1 D. 0
2.(3分)如图,直线a∥b,∠1=70°,那么∠2的度数是( )
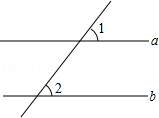
A. 50° B. 60° C. 70° D. 80°
3.(3分)下列根式中,与3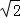 是同类二次根式的是( )
是同类二次根式的是( )
A. 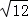 B.
B. 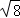 C.
C. 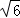 D.
D. 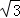
4.(3分)下列运算正确的是( )
A. a﹣2a=a B. (﹣2a2)3=﹣8a6 C. a6+a3=a2 D. (a+b)2=a2+b2
5.(3分)如图所示的是三通管的立体图,则这个几何体的俯视图是( )
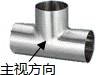
A.  B.
B.  C.
C.  D.
D. 
6.(3分)因式分解a3﹣a的结果是( )
A. a2 B. a(a2﹣1) C. a(a+1)(a﹣1) D. a(a﹣1)2
7.(3分)在平面直角坐标系中,点A(﹣1,2)关于x轴对称的点B的坐标为( )
A. (﹣1,2) B. (1,2) C. (1,﹣2) D. (﹣1,﹣2)
8.(3分)在2013年“崇左市初中毕业升学体育考试”测试中,参加男子掷实心球的10名考生的成绩记录如下(单位:米):7.5、6.5、8.2、7.8、8.8、8.2、8.6、8.2、8.5、9.5,则该组数据的众数、中位数、平均数依次分别是( )
A. 8.2、8.0、7.5 B. 8.2、8.5、8.1 C. 8.2、8.2、8.15 D. 8.2、8.2、8.18
9.(3分)一副三角板按如图方式摆放,且∠1的度数比∠2的度数大50°,若设∠1=x°,∠2=y°,则可得到方程组为( )
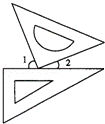
A.  B.
B. 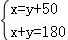 C.
C. 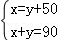 D.
D. 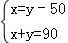
10.(3分)若反比例函数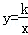 的图象经过点(m,3m),其中m≠0,则此反比例函数图象经过( )
的图象经过点(m,3m),其中m≠0,则此反比例函数图象经过( )
A. 第一、三 象限 B. 第一、二象限 C. 第二、四象限 D. 第三、四象限
象限 B. 第一、二象限 C. 第二、四象限 D. 第三、四象限
11.(3分)一个圆锥的侧面积是底面积的4倍,则圆锥侧面展开图的扇形的圆心角是( )
A. 60° B. 90° C. 120° D. 180°
12.(3分)如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形,则展开后的等腰三角形周长是( )

A. 12 B. 18 C. 2+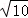 D. 2+2
D. 2+2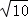
二、填空题(共6小题,每小题3分,满分18分)
13.(3分)函数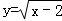 中,自变量x的取值范围是 x≥2 .
中,自变量x的取值范围是 x≥2 .
14.(3分)据军事网站报道,辽宁号航空母舰,简称“辽宁舰”,舷号16,是中国人民解放军海军第一艘可以搭载固定翼飞机的航空母舰.辽宁舰的满载排水量67500吨,将数据67500用科学记数法表示为 6.75×104.
15.(3分)据崇左市气象预报:我市6月份某天中午各县(区)市的气温如下:
地名 | 江州区 | 扶绥县 | 天等县 | 大新县 | 龙州县 | 宁明县 | 凭祥市 |
气温 | 37(℃) | 33(℃) | 30(℃) | 31(℃) | 33(℃) | 36 | 34(℃) |
则我市各县(区)市这组气温数据的极差是 7℃ .
16.(3分)等腰三角形的两边长分别是3和7,则其周长为 17 .
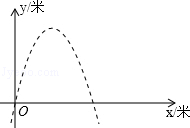
17.(3分)崇左市政府大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分.则水喷出的最大高度是 4 千米.
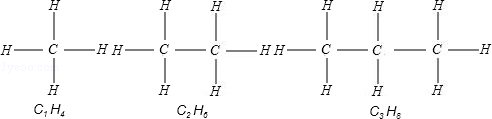
18.(3分)如图是三种化合物的结构式及分子式.请按其规律,写出后面第2013种化合物的分子式 C2013H4028 .
三、解答题(共8小题,满分66分,解答题应写出文字说明,证明过程或演算步骤)
19.(6分)计算:20130﹣(﹣3)﹣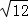 +
+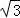 +
+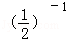 .
.
20.(6分)解不等式组: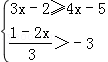 .
.
21.(6分)我市新城区环形路的拓宽改造工程项目,经投标决定由甲、乙两个工程队共同完成这一工程项目.已知乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍;该工程如果由甲队先做6天,剩下的工程再由甲、乙两队合作16天可以完成.求甲、乙两队单独完成这项工程各需要多少天?
22.(8分)如图所示,正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF.
(1)求证:△ADE≌△ABF;
(2)问:将△ADE顺时针旋转多少度后与△ABF重合,旋转中心是什么?
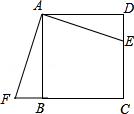
23.(8分)自古以来,钓鱼岛及其附属岛屿都是我国固有领土.如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了800米,在点D测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.
(结果精确到0.1米,参考数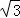 ≈1.73,
≈1.73,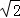 ≈1.41)
≈1.41)

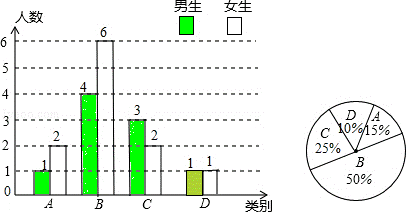
24.(10分)我市自从去年九月实施高中新课程改革以来,高中学生在课堂上的“自主学习、合作交流”能力有了很大提高.张老师为了了解所教班级学生的“自主学习、合作交流”的具体情况,对该班部分学生进行了为期一个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差,且将调查结果绘制成以下两幅不完整的统计图.请你根据统计图解答下列问题: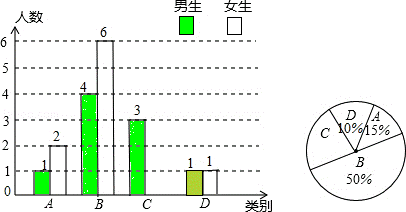
(1)本次调查中,张老师一共调查了 20 名学生,其中C类女生有 2 名;
(2)请将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
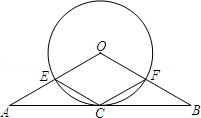
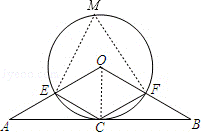
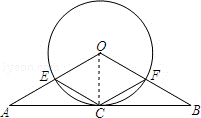
25.(10分)如图,在△ABO中,OA=OB,C是边AB的中 点,以O为圆心的圆过点C,且与OA交于点E,与OB交于点F,连接CE,CF.
点,以O为圆心的圆过点C,且与OA交于点E,与OB交于点F,连接CE,CF.
(1)求证:AB与⊙O相切.
(2)若∠AOB=∠ECF,试判断四边形OECF的形状,并说明理由.
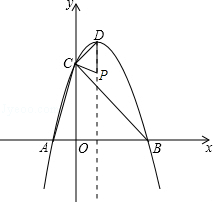
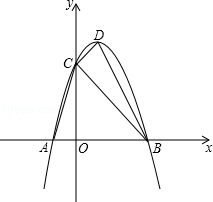
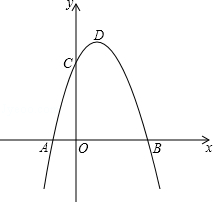
26.(12分)抛物线y=﹣x2平移后的位置如图所示,点A,B坐标分别为(﹣1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.
(1)求平移后的抛物线的解析式和点D的坐标;
(2)∠ACB和∠ABD是否相等?请证明你的结论;
(3)点P在平移后的抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.
一、选择题(共12小题,每小题3分,满分36分。每小题都给出代号为A、B、C、D四个结论,其中只有一个是正确的。)
1.A
2.C
3.B
4.B
5.A
6.C
7.D
8.D
9.C
10.A
11.B
12.D
二、填空题(共6小题,每小题3分,满分18分)
13. x≥2
14. 6.75×104.
15.7℃
16.17
17.4
18.C2013H4028
三、解答题(共8小题,满分66分,解答题应写出文字说明,证明过程或演算步骤)
19.解:原式=1+3﹣2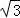 +
+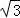 +2=6﹣
+2=6﹣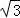
20.解: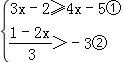 ,
,
由①得,x≤3;
由②得,x≤5,
故此不等式组的解集为:x≤3.
21.解:设乙工程队单独完成这项工程需要x天,则甲工程队单独完成这项工程需要2x天,由题意得:
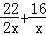 =1
=1
解得:x=17,
经检验:x=17是分式方程的解,
答:乙工程队单独完成这项工所需要17天.
22.(1)证明:在正方形ABCD中,
∠D=∠ABC=90°,
∴∠ABF=90°,
∴∠D=∠ABF=90°,(3分)
又DE=BF,AD=AB,(4分)
∴△ADE≌△ABF.(5分)
(2)解:将△ADE顺时针旋转90后与△ABF重合,(7分)旋转中心是点A.(9分)
23.解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,

∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF,
由题意可知:AE=BF=100米,CD=800米.
在Rt△AEC中,∠C=60°,AE=100米.
∴CE=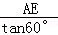 =
=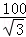 =
=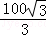 (米).
(米).
在Rt△BFD中,∠BDF=45°,BF=100.
∴DF=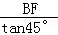 =
=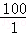 =100(米).
=100(米).
∴AB=EF=CD+DF﹣CE=800+100﹣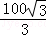 ≈900﹣
≈900﹣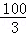 ×1.73≈900﹣57.67≈842.3米.
×1.73≈900﹣57.67≈842.3米.
答:岛屿两侧端点A、B的距离为842.3米.
24.解:(1)调查学生数为3 ÷15%=20(人),
÷15%=20(人),
“C”类别学生数为20×(1﹣10%﹣15%﹣50%)=5(人),其中男生有3人,
C类女生有5﹣3=2(人);
(2)C类女生有2人,C类所占的百分比为1﹣10%﹣15%﹣50%=25%.补充统计图如下图所示;
(3)根据张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,画树状图如下:
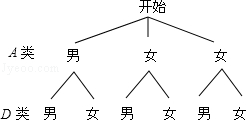
一共有6种等可能的结果:男男、男女、女男、女女、女男、女女,其中一男一女的情况有3种,
P(一男一女)==.
故答案为:20,2.
25.(1)证明:连接OC,
∵在△ABO中,OA=OB,C是边AB的中点,
∴OC⊥AB,
∵OC为半径,
∴AB与⊙O相切;
(2)解:四边形OECF的形状是菱形,
理由是:
如图,取圆周角∠M,
则∠M+∠ECF=180°,
由圆周角定理得:∠EOF=2∠M,
∵∠ECF=∠EOF,
∴∠ECF=2∠M,
∴3∠M=180°,
∠M=60°,
∴∠EOF=∠ECF=120°,
∵OA=OB,
∴∠A=∠B=30°,
∴∠EOC=90°﹣30°=60°,
∵OE=OC,
∴△OEC是等边三角形,
∴EC=OE,
同理OF=FC,
即OE=EC=FC=OF,
∴四边形OECF是菱形.
26.解:(1)∵将抛物线y=﹣x2平移,平移后的抛物线与x轴交于点A(﹣1,0)和点B(3,0),
∴平移后的抛物线的表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3,即y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4);
(2)∠ACB与∠ABD相等,理由如下:
如图,∵y=﹣ x2+2x+3,
x2+2x+3,
∴点x=0时,y=3,即C点坐标为(0,3),
又∵B(3,0),∠BOC=90°,
∴OB=OC,∠OBC=∠OCB=45°.
在△BCD中,∵BC2=32+32=18,CD2=12+12=2,BD2=22+42=20,
∴BC2+CD2=BD2,
∴∠BCD=90°,
∴tan∠CBD=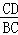 =
=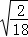 =,
=,
∵在△AOC中,∠AOC=90°,
∴tan∠ACO=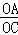 =,
=,
∴tan∠ACO=tan∠CBD,
∴∠ACO=∠CBD,
∴∠ACO+∠OCB=∠CBD+∠OBC,
即∠ACB=∠ABD;
(3)∵点P在平移后的抛物线的对称轴上,而y=﹣x2+2x+3的对称轴为x=1,
∴可设P点的坐标为(1,n).
∵△ABC是锐角三角形,
∴当△CDP与△ABC相似时,△CDP也是锐角三角形,
∴n<4,即点P只能在点D的下方,
又∵∠CDP=∠ABC=45°,
∴D与B是对应点,分两种情况:
①如果△CDP∽△ABC,那么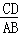 =
=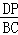 ,
,
即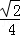 =
=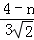 ,
,
解得n=,
∴P点的坐标为(1,);
②如果△CDP∽△CBA,那么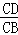 =
=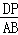 ,
,
即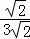 =
=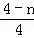 ,
,
解得n=,
∴P点的坐标为(1,).
综上可知P点的坐标为(1,)或(1,).