一、选择题：本大题共10小题，每小题3分，共30分.

二．填空题：本大题共8小题，每小题4分，共32分.

11. 2(a-1)2 12. x+2 13. 8 14. 1

15. 60° 16. -1或-7 17. 12 18. 552 (或3025)

三、解答题（一）：本大题共5小题，共38分，解答时，应写出必要的文字说明、证明过程或演算步骤．(注：解法合理、答案正确均可得分)

19．解：原式=-8++3　　 ……………………………………………3分

= -5　　　 …………………………………………………6分

20．解：由题意得

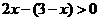……………………………………………………3分

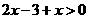……………………………………………………4分

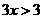……………………………………………………5分

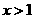………………………………………………………6分

21.

（1）解：如图所示，DE就是要求作的AB边上的垂直平分线； …………4分

（2）证明：

∵DE是AB边上的垂直平分线，∠A=30°

∴AD=BD

∴∠ABD=∠A=30°. ………………………………6分

∵∠C=90°

∴∠ABC=90°-∠A=90°-30°=60°

∴∠CBD=∠ABC-∠ABD=60°-30°=30°

∴∠ABD=∠CBD

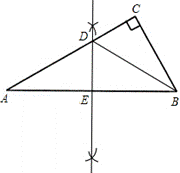
第21题图

即BD平分∠CBA ……………………………………………………………8分

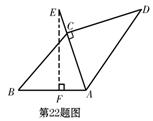
22．解：（1）AD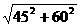＝＝75(cm) …………………3分

∴ 车架档AD的长是75cm. ……………………4分

（2）过点E作EF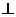AB，垂足为F ………………5分

=62.79≈63(cm) ………………………………7分

∴ 车座点E到车架档AB的距离约是63cm． ………8分

23．解：（1）∵直线 y=mx与双曲线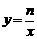相交于A(-1，a)、B两点

∴A、B两点关于原点O对称

∵A(-1，a), ∴B点横坐标为1.而BC⊥x轴，∴C(1，0) ………2分

∵△AOC的面积为1，∴A(-1，2) ………………………………………3分

将A(-1，2)代入y=mx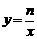，，可得m＝-2，n＝-2 ……………………5分

（2）设直线AC的解析式为： y＝kx＋b（k≠0）? ……………………6分

∵y＝kx＋b经过点A（-1，2）、C（1，0）

∴

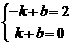
解得k＝-1，b＝1 ………………………………………………9分

∴直线AC的解析式为 ……………………………………………10分

四、解答题（二）：本大题共5小题，共50分，解答时，应写出必要的文字说明、证明过程或演算步骤

24.解：方法一（画树状图）：

y x (x ,y)	1	2	3	4
1		(1,2)	(1,3)	(1,4)
2	(2,1)		(2,3)	(2,4)
3	(3,1)	(3,2)		(3,4)
4	(4,1)	(4,2)	(4,3)

方法二（列表）：

…………………………………2分

（1）点P所有可能的坐标有： （1，2），（1，3），（1，4）,（2，1），（2，3），（2，4），（3，1），（3，2），（3，4）,（4，1），（4，2），（4，3）共12种 …………4分

（2）∵共有12种等可能的结果，其中在函数y=﹣x+5图象上的有4种，

即：（1，4）,（2，3），（3，2），（4，1） ……………………………6分

∴点P（x，y）在函数y=﹣x+5图象上的概率为：P= …………8分

25. 解：（1） 200 …………………………………………………………………2分

（2）C ………………………………………………………………………………4分

C的条形高度改为50 …………………………………………………………… 6分

（3）画出人数为30条形D ……………………………………………………… 8分

（4）600×（20%+40%）=360(人) ……………………………………………9分

答：该校对此活动“非常喜欢”和“比较喜欢”的学生有360人. ………………10分

26. 解：（1）证明：∵D、E分别是AB、AC边的中点

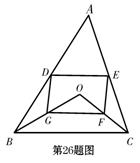
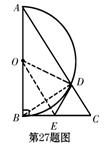
∴DE∥BC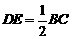，. ……………………………2分

同理，GF∥BC， ………………………4分

∴DE∥GF，DE=GF …………………………………5分

∴四边形DEFG是平行四边形 ………………………6分

（2）当OA=BC时

平行四边形DEFG是菱形 …………………………10分

27．（1）证明：连接OD、OE、BD ………………………………1分

∵AB为半圆的直径

∴∠ADB=∠BDC=90° ……………………………2分

在Rt△BDC中，E为斜边BC的中点

∴DE=BE ………………………………………………………………………………3分

在△OBE和△ODE中

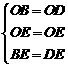
∴△OBE≌△ODE（SSS）

∴∠ODE=∠ABC=90°

则DE为半圆的切线……………………………………5分

（2）在Rt△ABC中，∠BAC=30°

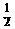∴BC=AC

∵BC=2DE=4

∴AC=8 …………………………………………………………………………7分

又∵∠C=60°，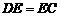

∴△DEC为等边三角形，即DC=DE=2 …………………………………9分

则AD=AC-DC=6． ……………………………………………………………10分

注：证明及计算方法正确均可得分.

28. 解：（1）解析式为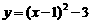，顶点坐标为M（1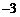，）， ……………2分

A（0，），B（3，1）. ……………………………………4分

（2）过点B、M分别作y轴的垂线，垂足分别为E、F.

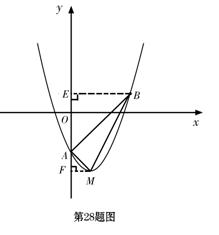
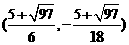∵ EB=EA=3，∴ ∠EAB=∠EBA=45°.

同理∠FAM=∠FMA=45°.

∴ △FAM ∽ △EAB，∴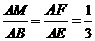

∵ ∠EAB=∠FAM=45°，∴ ∠BAM=90° ，…6分

∴Rt△ABM中，

∠ABM = ……………8分

（3）过点P作PH⊥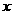轴，垂足为H .

设点P坐标为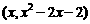 ………………9分

① 当点P在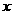轴上方时，

由题意得 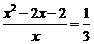，解得（舍），.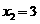

∴点P坐标为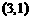 ……………………………………………………………10分

② 当点P在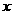轴下方时，

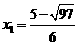题意得 ，解得（舍），.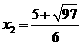

∴点P坐标为 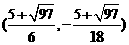…………………………………………11分

综上所述，P点坐标为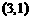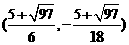，…………………………12分

注：证明及计算方法正确均可得分.