一、选择题

1．计算－4×（－2）的结果是 （　　）

A．8 B．－8 C．6 D．－2

2．如图，由相同的小正方体搭成的几何体的主视图是 （　　）

3．如图，跷跷板AB的支柱OD经过它的中点O，且垂直于地面BC，垂足为D，OD＝50cm，当它的一端B着地时，另一端A离地面的高度AC为 （　　）

A．25cm B．50cm C．75cm D．100cm

4．下列整数中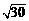，与最接近的是 （　　）

A．4 B．5 C．6 D．7

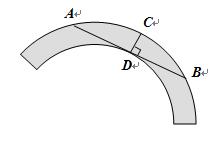
5．从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是 （　　）

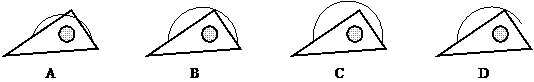
6．某品牌电插座抽样检查的合格率为99%，则下列说法中正确的是（　　）

A．购买100个该品牌的电插座，一定有99个合格

B．购买1000个该品牌的电插座，一定有10不个合格

C．购买20个该品牌的电插座，一定都合格

D．即使购买1个该品牌的电插座，也可能不合格

7．将分式方程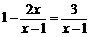去分母，得到正确的整式方程是······· （　　）

A．1－2x＝3 B．x－1－2x＝3 C．1+2x＝3 D．x－1+2x＝3

8．如图，把一个小球垂直向上抛出，则下列描述该小球的运动速度v（单位∶m/s）与运动时间t（单位s）关系的函数图像中，正确的是（　　）

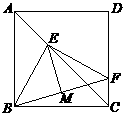
9．如图，F是正方形ABCD的边CD上的一个动点，BF的垂直平分线交对角线AC于点E，连接BE，BF，则EBF的度数是 （　　）

A．45° B．50° C．60° D．不确定

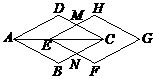
10．如图，菱形ABCD的对角线AC＝4cm，把它沿着对角线AC方向平移1cm，得到菱形EFGH，则图中阴影部分图形的面积与四边形EMCN的面积之比为····················· （　　）

A．4∶3 B．3∶2 C．14∶9 D．17∶9

二、填空题（本题有6小题，每小题5分，共30分）

11．计算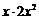的结果是＿＿＿＿．

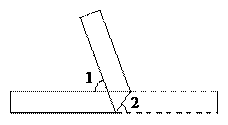
12．如图折叠一张矩形纸片，已知∠1＝70°，则∠2的度数是＿＿＿＿．

13．因式分解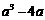的结果是＿＿＿＿．

14．抽屉里放着黑白两种颜色的袜子各1双（除颜色外其余都相同）在看不见的情况下随机摸出两只袜子，他们恰好同色的概率是＿＿＿＿．

15．如图是一个古代车轮的碎片，小时为求其外圆半径，连结外圆上的两点A、B，并使AB与车轮内圆相切于点D，作CD⊥AB交外圆与点C，测得CD＝10cm，AB＝60cm，则这个外圆半径为＿＿＿＿cm．

16．有一个计算程序，每次运算都是把一个数先乘以2，再乘以它与1的和，多次重复进行这种运算的过程如下∶

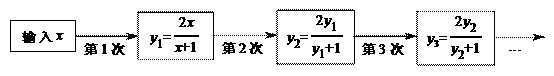
则第n次的运算结果＝＿＿＿＿（含字母x和n的代数式表示）．

三、解答题（本题有8小题，第17－20每题8分，第21题10分，第22，23每题12分，第24题14分，共80分）

17．计算∶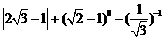

18．解不等式组∶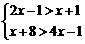，并把解集在下面数轴上表示出来．

19．已知反比例函数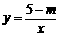，当x=2时y＝3．

（1）求m的值；（2）当3≤x≤6时，求函数值y的取值范围．

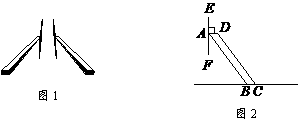
20．如图1是某公共汽车前挡风玻璃的雨刮器，其工作原理如图2，雨刷EF丄AD，垂足为A，AB＝CD，且AD＝BC．这样能使雨刷EF在运动时．始终垂直于玻璃窗下沿BC．请证明这一结论．

21．如图，某翼装飞行运动员从离水平地面高AC＝500m的A处出发，沿着俯角为15°的方向，直线滑行1600米到达D点，然后打开降落伞以75°的俯角降落到地面上的B点．求他飞行的水平距离（结果精确到1m）．

22．为了估计鱼塘中成品鱼（个体质最在0.5kg及以上，下同〉的总质量，先从鱼塘中捕捞50条成品鱼．称得它们的质ft如下表∶

质量/kg 0.5 0.6 0.7 1.0 1.2 1.6 1.9

数量/条 1 8 15 18 5 1 2

然后做上记号再放回水库中，过几天又捕捞了100条成品鱼，发现其中2条带有记号．

（1）请根据表中数据补全下面的直方图（各组中数据包括左端点不包括右端点）．

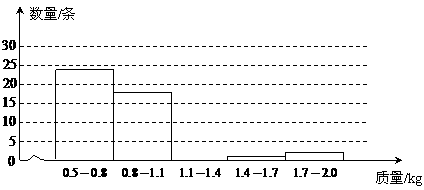
（2）根据图中数据分组．估计从鱼塘中随机捕一条成品鱼，其质里落在哪一组的可能性最大?

（3）根据图中数据分组，估计鱼塘里质量中等的成品鱼，其质量落在哪一组内？

（4）请你用适当的方法估计鱼塘中成品鱼的总质撒（精确到1kg）．

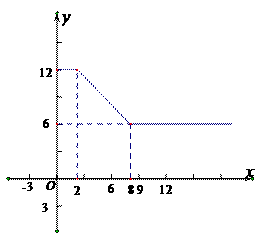
23．某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类，A类杨梅包装后直接销售，B类杨梅深加工再销售．A类杨梅的包装成本为1万元/吨，根据市场调查，它的平均销售价格y（单位∶万元/吨）与销售数量x（x≥2）（取位∶吨）之间的函数关系式如图，B类杨梅深加工总费用s（单位:万元）与加工数量t（单位∶吨）之间的函数关系是s＝12＋3t，平均销售价格为9万元/吨．

（1）直接写出A类杨梅平均销售价格y与销售量x这间的函数关系式．

（2）第一次，该公司收购了20吨杨梅，其中A类杨梅x吨，经营这批杨梅所获得的毛利润为w万元（毛利润＝销售总收人－经营总成本）．

①求w关于x的函数关系式

②若该公司获得了30万元毛利润，问∶用于直销的A类杨梅有多少吨？

（3）第二次该公司准备投人132万元资金，请设计－种经营方案，使公司获得最大毛利润，并求出最大毛利润．

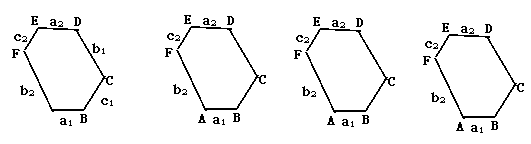
24．研究几何图形，我们往往先给出这类图形的定义，再研究它的性质和判定．

定义∶六个内角相等的六边形叫等角六边形．

（1）研究性质

①如图1，等角六边形ABCDEF中，三组正对边AB与DE，BC与EF，CD与AF分别有什么位置关系？证明你的结论．

②如图2，等角六边形ABCDEF中，如果有AB＝DE，则其余两组正对边BC与EF，CD与AF相等吗？证明你的结论．

③如图3，等角六边形ABCDEF中．如果三条正对角线AD，BE，CF相交于一点O，那么三组正对边AB与DE，BC与EF，CD与AF分别有什么数量关系？证明你的结论．

（2）探索判定

三组正对边分别平行的六边形，至少需要几个内角为120°才能保证该六变形—定是等角六边形？