(单词翻译:单击)
卷I (选择题,共42分)
一、选择题(本大题共16个小题,1-6小题,每小题2分;7-16小题,每小题3分,共42分,在每小题给出的四个选项中,只有一项符合题目要求的)
1、-2是2的( )
A、倒数 B、相反数
C、绝对值 D、平方根
2、如图,△ABC中,D,E分别上边AB,AC的中点,若DE=2,则BC= ( )
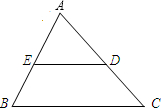
A、2 B、3 C、4 D、5
3、计算:85²-15²= ( )
A、70 B、700 C、4900 D、7000
4、如图,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角上( )
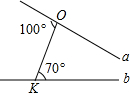
A、20° B、30 ° C、70° D、80°
5、a,b是两个连续整数,若a<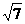 <b,则a,b分别是( )
<b,则a,b分别是( )
A、2,3 B、3,2 C、3,4 D、6,8
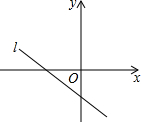
6、如图,直线l经过第二,三,四象限,l的解析式是y=(m-2)x+n,则m的取值范围则数轴上表示为( )
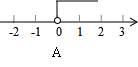
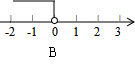
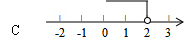
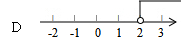
7、化简: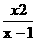 -
-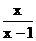 ( )
( )
A、0 B、1 C、x D、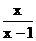
8、如图,将长为2,宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n≠( )
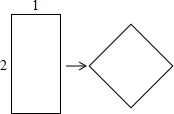
A、2 B、3 C、4 D、5
9、某种正方形合金板材的成本y(元)与它的面积成成正比,设边长为x厘米,当x=3时,y=18,那么当成本为72元时,边长为( )
A、6厘米 B、12厘米 C、24厘米D、36厘米
10、图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A,B在围成的正方体的距离是( )
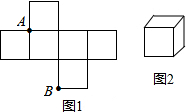
A、0 B、1 C、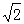 D、
D、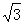
11、某小组作“用频率估计概率的实验时,统计了某一结果出现的频率,绘制了如图 所示的折线统计图,则符合这一结果的实验最有可能的是( )
所示的折线统计图,则符合这一结果的实验最有可能的是( )
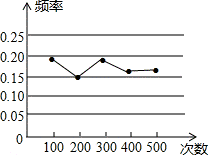
A 、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃;
C、暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球。
D、掷一个质地均匀的正六面体骰子,向上的面点数是4.
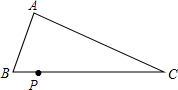
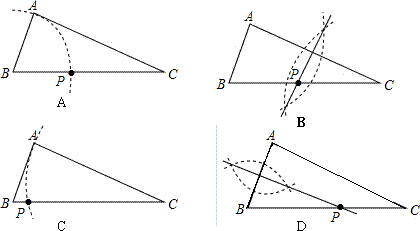
12、如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
13、在研究相似问题时,甲、 乙两同学的观点如下:
乙两同学的观点如下:
甲:将边长为3,4,5的三角形按图中的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似。
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形 与原矩形不相似.
与原矩形不相似.
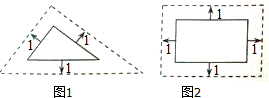
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对
C.甲对,乙不对 D.甲不对,乙对
14、定义新运算:a⊕b= 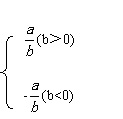 例如:4⊕5=
例如:4⊕5=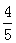 ,4⊕(-5)=
,4⊕(-5)=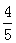 .则函数y=2⊕x(x≠0)的图象大致是( )
.则函数y=2⊕x(x≠0)的图象大致是( )
A、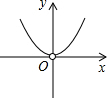 B、
B、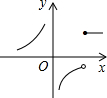
C、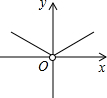 D、
D、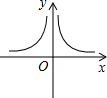
15、如图,边长为a的正六边形内有两个三角形,(数据如图),则
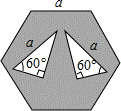
A、3 B、4 C、5 D、6
16、五名学生投篮球,规定每人投20 次,统计他们每人投中的次数,得到五个数据,若这五个数据的中位数是6,为一众数是7,则他们投中次数的总和可能是( )
次,统计他们每人投中的次数,得到五个数据,若这五个数据的中位数是6,为一众数是7,则他们投中次数的总和可能是( )
A、20 B、28 C、30 D、31
卷Ⅱ
一、填空题(本大题共4个小题,每小题3分,把答案写在题中横线上)
17、计算: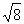 ×
×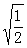 = ______________。
= ______________。
18、若实数m,n满足|m-2|+(n-2 014)²=0.则m-1+n0= _____________ 。
014)²=0.则m-1+n0= _____________ 。
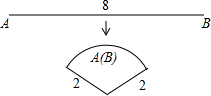
19、如图,将长为8cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形= _____________cm²
20、如图,点O,A在数轴上表示的数分别是0, 0.1,将线段OA分成100等份,其分点由左向右依次为M1,M2……M99;将线段O M1分成100等份,其分点由左向右依次为N1,N2……N99,将线段O N1分成100等份,其分点由左向右依次为P1,P2……P99,则点P1所表示的数用科学计数法表示为______________。
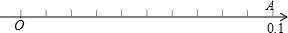
三、解答题(本大题共6个小题,共66分,解答应写出文字说明、证明过程或演算步骤)
21、嘉淇同学用配方法推导一元二次方程ax²+bx+c=0(a≠0)的求根公式时,对于b2-4ac>0的情况,她是这样做的:

(1)嘉淇的解法从第_______步开始出现错误;事实上,当b2-4ac>0时,方程ax²+bx+c=0(a≠0)的求根公式是 ____________。
(2)用配方法解方程:x2-2x-24=0
22、(本小题满分10分)
如图,A,B,C是三个垃圾存放点,点B,C分别位于点A的正北和正东方向,AC=100米,四人分别测得∠C的度数如下表:
甲 | 乙 | 丙 | 丁 | |
∠C(单位:度) | 34 | 36 | 38 | 40 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图,如下图。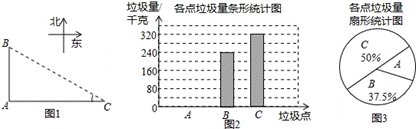
(1)求表中∠C度数的平均数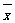 :
:
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的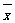 作
作 为∠C的度数
为∠C的度数 ,要
,要 将A处的垃圾
将A处的垃圾 沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
23、(本小题满分11分)
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接BD,CE交于点F。
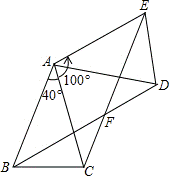
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形。
24、(本小题满分11分)
如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点,抛物线l的解析式为y=(-1)nx²+bx+c(n为整数)。
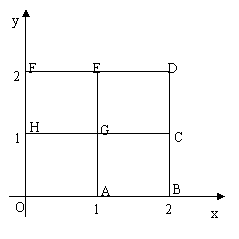
(1)n为奇数且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线的顶点。
(2)n为偶数,且l经过点A(1,0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是、是否在该抛物线上。
(3)若l经过九个格点中的三个,直接写出所有满足这样条件的抛物线条数。
25.(本小题满分11分)
 如图,优弧A B 所在☉O的半径为2,AB=2
如图,优弧A B 所在☉O的半径为2,AB=2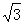 点P为优弧A B上一点(点P不与A,B重合)将图形沿BP折叠,得到点A的对称点A’
点P为优弧A B上一点(点P不与A,B重合)将图形沿BP折叠,得到点A的对称点A’
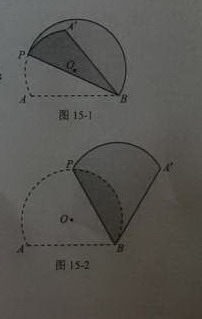
(1)点O到弦AB的距离是 ____________;当BP经过点O时,∠ABA’= ___________。
(2)当BA’与 ☉O相切时,如图所示,求折痕BP的长;
☉O相切时,如图所示,求折痕BP的长;
(3)若线段BA’与优弧AB只有一个公共点B,设∠ABP=α,确定α的取值范围。
26.(本小题满分13分)
某景区的环形路是边长为800米的正方形ABCD,如图,现有1号,2号两游览车分别从出口A和经典C同时出发,1号车顺时针,2号车逆时针沿环形路连续循环行驶,供游客随时乘车(上,下车的时间忽略不计),两车的速度均为200米/分。探 究:设行驶时间为t分
究:设行驶时间为t分

(1)当0≤t≤s时,分别写出1号车,2号车在左半环线离出口A的路程y1,y2(米)与t(分)的函数关系式,并求出当两车相距的路程是400米时t的值;
(2)t为何值时,1号车第三次恰好经过点C?,并直接写出这一段时间内它与2号车相遇过的次数。
发现如图,游客甲在BC上一点K(不与点B,C重合)处候车,准备乘车到出口A,设CK=x米。
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车;
比较哪种情况用时较多?(含候车时间)
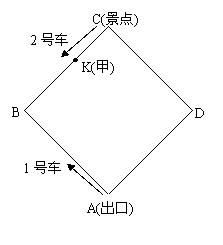
决策已知游客乙 在DA上从D向出口A走去,步行的速度是50米/分,当行进到DA上一点P(不与D,A重合)时,刚好与2号车相遇。
在DA上从D向出口A走去,步行的速度是50米/分,当行进到DA上一点P(不与D,A重合)时,刚好与2号车相遇。
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由;
(2)设PA=s(0<s<800)米,若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中,他该如何选择?