(单词翻译:单击)
一、选择题(本大题共12小题,每题3分,共36分.只有一项是符合题目要求的.)
1.5的倒数为()
A. 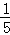 B. 5 C.
B. 5 C. 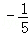 D.﹣5
D.﹣5

2.计算x2•x3的结果为()
A. 2x2 B. x5 C. 2x3 D.x6
【考点】同底数幂的乘法.
【分析】根据同底数幂的乘法底数不变指数相加,可得答案.
【详解】解:原式=x2+3=x5.
故选:B.
【点评】本题考查了同底数幂的乘法,底数不变指数相加是解题关键.
3.如图的几何图形的俯视图为()

A. B.
B.  C
C D.
D.
【考点】简单组合体的三视图.
【分析】根据从上面看得到的图形是俯视图,可得俯视图.
【详解】解:从上面看:里边是圆,外边是矩形,
故选:C.
【点评】本题考查了简单组合体的三视图,注意所有的看到的棱都应表现在俯视图中.
4.某校八年级(2)班6名女同学的体重(单位:kg)分别为35,36,40,42,42,则这组数据的中位数是()
A. 38 B. 39 C. 40 D.42
【考点】中位数.
【分析】根据中位数的定义求解,把数据按大小排列,第3个数为中位数.
【详解】解:题目中数据共有5个,中位数是按从小到大排列后第3个数作为中位数,故这组数据的中位数是40.
故选C.
【点评】本题属于基础题,考查了确定一组数据的中位数的能力.要明确定义:将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数,比较简单.
5.如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为()
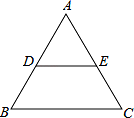
A.30°B. 60°C. 120°D.150°
【考点】三角形中位线定理;平行线的性质;等边三角形的性质.
【分析】根据等边三角形的性质,可得∠C的度数,根据三角形中位线的性质,可得DE与BC的关系,根据平行线的性质,可得答案.
【详解】解:由等边△ABC得∠C=60°,
由三角形中位线的性质得DE∥BC,
∠DEC=180°﹣∠C=180°﹣60°=120°,
故选:C.
【点评】本题考查了三角形中位线定理,三角形的中位线平行于第三边且等于第三边的一半.
6.已知实数x、y满足 +|y+3|=0,则x+y的值为()
+|y+3|=0,则x+y的值为()
A.﹣2B. 2C. 4D.﹣4
【考点】非负数的性质:算术平方根;非负数的性质:绝对值.
【分析】根据非负数的性质,可求出m、n的值,然后将代数式化简再代值计算.
【详解】解:∵ +|y+3|=0,
+|y+3|=0,
∴x﹣1=0,y+3=0;
∴x=1,y=﹣3,
∴原式=1+(﹣3)=﹣2
故选:A.
【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.
7.一个圆锥的底面半径是6cm,其侧面展开图为半圆,则圆锥的母线长为()
A.9cmB.12cmC.15cmD.18cm
【考点】圆锥的计算.
【分析】圆锥的母线长=圆锥的底面周长×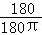 .
.
【详解】解:圆锥的母线长=2×π×6×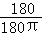 =12cm,
=12cm,
故选B.
【点评】本题考查圆锥的母线长的求法,注意利用圆锥的弧长等于底面周长这个知识点.
8.已知抛物线y=x2﹣2x+m+1与x轴有两个不同的交点,则函数y=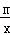 的大致图象是()
的大致图象是()
A. 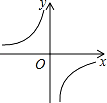 B.
B. 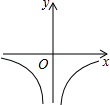 C
C D.
D. 
【考点】反比例函数的图象;抛物线与x轴的交点.
【分析】根据抛物线与x轴有两个不同的交点,可得判别式大于零,可得m的取值范围,根据m的取值范围,可得答案.
【详解】解:抛物线y=x2﹣2x+m+1与x轴有两个不同的交点,
∴△=(﹣2)2﹣4(m+1)>0
解得m<0,
∴函数y=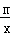 的图象位于二、四象限,
的图象位于二、四象限,
故选:A.
【点评】本题考查了反比例函数图象,先求出m的值,再判断函数图象的位置.
9.“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,当他们离目的地还有20千米时,汽车一共行驶的时间是()
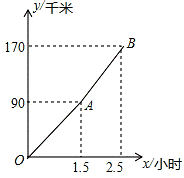
A. 2小时B. 2.2小时C. 2.25小时D.2.4小时
【考点】一次函数的应用.
【分析】根据待定系数法,可得一次函数解析式,根据函数值,可得相应自变量的值.
【详解】解:设AB段的函数解析式是y=kx+b,
y=kx+b的图象过A(1.5,90),B(2.5,170),
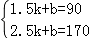 ,
,
解得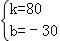
∴AB段函数的解析式是y=80x﹣30,
离目的地还有20千米时,即y=170﹣20=150km,
当y=150时,80x﹣30=150
x=2.25h,
故选:C.
【点评】本题考查了一次函数的应用,利用了待定系数法求解析式,利用函数值求自变量的值.
10.如图,⊙O1,⊙O2的圆心O1,O2都在直线l上,且半径分别为2cm,3cm,O1O2=8cm.若⊙O1以1cm/s的速度沿直线l向右匀速运动(⊙O2保持静止),则在7s时刻⊙O1与⊙O2的位置关系是()

A.外切B.相交C.内含D.内切
【考点】圆与圆的位置关系.
【分析】根据两圆的半径和移动的速度确定两圆的圆心距的最小值,从而确定两圆可能出现的位置关系,找到答案.
【详解】解:∵O1O2=8cm,⊙O1以1cm/s的速度沿直线l向右运动,7s后停止运动,
∴7s后两圆的圆心距为:1cm,
此时两圆的半径的差为:3﹣2=1cm,
∴此时内切,
故选D.
【点评】本题考查了圆与圆的位置关系,解题的关键是根据圆的移动速度确定两圆的圆心距,然后根据圆心距和两圆的半径确定答案.
11.如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则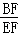 的值是()
的值是()

A.  B.
B.  C.
C. 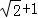 D.
D.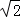


【点评】本题主要考查了平行线分线段成比例,全等三角形及角平分线的知识,解题的关键是找出线段之间的关系,CB=GB,AB=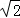 BC再利用比例式求解..
BC再利用比例式求解..
12.如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为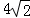 ,则a的值是()
,则a的值是()
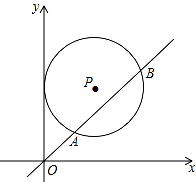
A. 4B.  C.
C.  D.
D.
【考点】 垂径定理;一次函数图象上点的坐标特征;勾股定理.
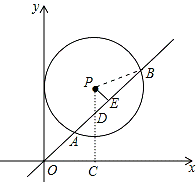
【分析】PC⊥轴于C,交AB于D,作PE⊥AB于E,连结PB,由于OC=3,PC=a,易得D点坐标为(3,3),则△OCD为等腰直角三角形,△PED也为等腰直角三角形,
由PE⊥AB,根据垂径定理得AE=BE= AB=2
AB=2 ,在Rt△PBE中,利用勾股定理可计算出PE=1,则PD=
,在Rt△PBE中,利用勾股定理可计算出PE=1,则PD= PE=
PE= ,所以a=3+
,所以a=3+ .
.
【详解】解:作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,如图,
∵⊙P的圆心坐标是(3,a),
∴OC=3,PC=a,
把x=3代入y=x得y=3,
∴D点坐标为(3,3),
∴CD=3,
∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE= AB=
AB= ×4
×4 =2
=2 ,
,
在Rt△PBE中,PB=3,
∴PE=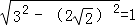 ,
,
∴PD= PE=
PE= ,
,
∴a=3+ .
.
故选B.
【点评】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和等腰直角三角形的性质.
13.分解因式:3a2+6a+3=_________.
【考点】提公因式法与公式法的综合运用.
【分析】先提取公因式3,再对余下的多项式利用完全平方公式继续分解.
【详解】解:3a2+6a+3,
=3(a2+2a+1),
=3(a+1)2.
故答案为:3(a+1)2.
【点评】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
14.使函数y= +
+ 有意义的自变量x的取值范围是_________.
有意义的自变量x的取值范围是_________.
【考点】函数自变量的取值范围.
【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
【详解】解:根据题意得:x+2≥0且(x﹣1)(x+2)≠0,
解得x≥﹣2,且x≠1,x≠﹣2,
故答案为:x>﹣2,且x≠1.
【点评】本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.
15.一个平行四边形的一条边长为3,两条对角线的长分别为4和 ,则它的面积为_________.
,则它的面积为_________.
【考点】菱形的判定与性质;勾股定理的逆定理;平行四边形的性质.
【分析】根据平行四边的性质,可得对角线互相平分,根据勾股定理的逆定理,可得对角星互相垂直,根据菱形的判定,可得菱形,根据菱形的面积公式,可得答案.
【详解】解:∵平行四边形两条对角线互相平分,
∴它们的一半分别为2和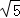 ,
,
∵22+(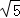 )2=32,
)2=32,
∴两条对角线互相垂直,
∴这个四边形是菱形,
S=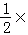 4×2
4×2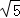 =4
=4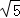 .
.
【点评】本题考查了菱形的判定与性质,利用了对角线互相垂直的平行四边形是菱形,菱形的面积是对角线乘积的一半.
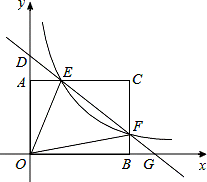
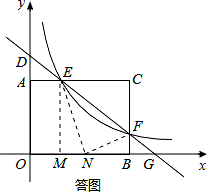
16.如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B、C重合),过点F的反比例函数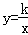 的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:
的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:
①若k=4,则△OEF的面积为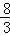 ;
;
②若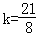 ,则点C关于直线EF的对称点在x轴上;
,则点C关于直线EF的对称点在x轴上;
③满足题设的k的取值范围是0<k≤12;
④若DE•EG= ,则k=1.
,则k=1.
其中正确的命题的序号是(写出所有正确命题的序号).
【考点】反比例函数综合题.
【分析】
(1)若k=4,则计算S△OEF= ≠
≠ ,故命题①错误;
,故命题①错误;
(2)如答图所示,若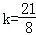 ,可证明直线EF是线段CN的垂直平分线,故命题②正确;
,可证明直线EF是线段CN的垂直平分线,故命题②正确;
(3)因为点F不经过点C(4,3),所以k≠12,故命题③错误;
(4)求出直线EF的解析式,得到点D、G的坐标,然后求出线段DE、EG的长度;利用算式DE•EG=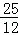 ,求出k=1,故命题④正确.
,求出k=1,故命题④正确.
【详解】解:命题①错误.理由如下:
∵k=4,
∴E(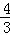 ,3),F(4,1),
,3),F(4,1),
∴CE=4﹣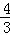 =
= ,CF=3﹣1=2.
,CF=3﹣1=2.
∴S△OEF=S矩形AOBC﹣S△AOE﹣S△BOF﹣S△CEF
=S矩形AOBC﹣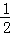 OA•AE﹣
OA•AE﹣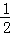 OB•BF﹣
OB•BF﹣ CE•CF
CE•CF
=4×3﹣ ×3×
×3× ﹣
﹣ ×4×1﹣
×4×1﹣ ×
×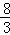 ×2=12﹣2﹣2﹣
×2=12﹣2﹣2﹣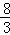 =
= ,
,
∴S△OEF≠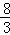 ,故命题①错误;
,故命题①错误;
命题②正确.理由如下:
∵k=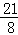 ,
,
∴E(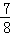 ,3),F(4,
,3),F(4,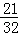 ),
),
∴CE=4﹣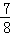 =
=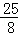 ,CF=3﹣
,CF=3﹣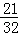 =
= .
.
如答图,过点E作EM⊥x轴于点M,则EM=3,OM=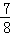 ;
;
在线段BM上取一点N,使得EN=CE=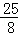 ,连接NF.
,连接NF.
在Rt△EMN中,由勾股定理得:MN=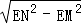 =
=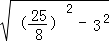 =
=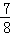 ,
,
∴BN=OB﹣OM﹣MN=4﹣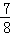 ﹣
﹣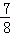 =
=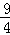 .
.
在Rt△BFN中,由勾股定理得:NF= =
=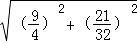 =
= .
.
∴NF=CF,
又∵EN=CE,
∴直线EF为线段CN的垂直平分线,即点N与点C关于直线EF对称,
故命题②正确;
命题③错误.理由如下:
由题意,点F与点C(4,3)不重合,所以k≠4×3=12,故命题③错误;
命题④正确.理由如下:
为简化计算,不妨设k=12m,则E(4m,3),F(4,3m).
设直线EF的解析式为y=ax+b,则有
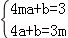 ,解得
,解得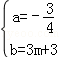 ,
,
∴y= x+3m+3.
x+3m+3.
令x=0,得y=3m+3,∴D(0,3m+3);
令y=0,得x=4m+4,∴G(4m+4,0).
如答图,过点E作EM⊥x轴于点M,则OM=AE=4m,EM=3.
在Rt△ADE中,AD=AD=OD﹣OA=3m,AE=4m,由勾股定理得:DE=5m;
在Rt△MEG中,MG=OG﹣OM=(4m+4)﹣4m=4,EM=3,由勾股定理得:EG=5.
∴DE•EG=5m×5=25m= ,解得m=
,解得m=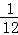 ,
,
∴k=12m=1,故命题④正确.
综上所述,正确的命题是:②④,
故答案为:②④.
【点评】本题综合考查了函数的图象与性质、反比例函数图象上点的坐标特征、比例系数k的几何意义、待定系数法、矩形及勾股定理等多个知识点,有一定的难度.本题计算量较大,解题过程中注意认真计算.
三、(本大题共3小题,每题6分,共18分)
17.(6分)计算: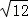 ﹣4sin60°+(π+2)0+(
﹣4sin60°+(π+2)0+(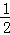 )﹣2.
)﹣2.
【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.
【分析】本题涉及零指数幂、负整指数幂、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
【详解】解:原式=2 ﹣4×
﹣4× +1+4
+1+4
=5.
【点评】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.
18.(6分)计算( ﹣
﹣ )÷
)÷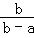 .
.
【考点】分式的混合运算.
【分析】首先把除法运算转化成乘法运算,然后找出最简公分母,进行通分,化简.
【详解】解:原式=( ﹣
﹣ )•
)•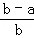
=( ﹣
﹣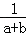 )•(﹣
)•(﹣ ),
),
=﹣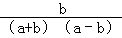 •
• ,
,
=﹣ .
.
【点评】此题主要考查了分式的混合运算,通分、因式分解和约分是解答的关键.
19.(6分)如图,正方形ABCD中,E、F分别为BC、CD上的点,且AE⊥BF,垂足为点G.
求证:AE=BF.
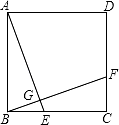
【考点】全等三角形的判定与性质;正方形的性质.
【分析】根据正方形的性质,可得∠ABC与∠C的关系,AB与BC的关系,根据两直线垂直,可得∠AGB的度数,根据直角三角形锐角的关系,可得∠ABG与∠BAG的关系,根据同角的余角相等,可得∠BAG与∠CBF的关系,根据ASA,可得三角形全等,根据全等三角形的性质,可得答案.
【详解】证明:∵正方形ABCD,
∴∠ABC=∠C,AB=BC.
∵AE⊥BF,
∴∠AGB=90°∠ABG+∠BAG=90°,
∵∠ABG+∠FNC=90°,
∴∠BAG=∠CBF.
在△ABE和△BCF中,
 ,
,
∴△ABE≌△BCF(ASA),
∴AE=BF.
【点评】本题考查了全等三角形的判定与性质,利用了正方形的性质,直角三角形的性质,余角的性质,全等三角形的判定与性质.
四、(本大题共1小题,每题7分,共14分)
20.(7分)某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)求出x的值,并将不完整的条形统计图补充完整;
(2)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数;
(3)若本次调查活动中,九年级(1)班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上,现从这5人中任选2人参加学校组织的知识抢答赛,求选出的2人来自不同小组的概率.
【考点】条形统计图;用样本估计总体;扇形统计图;列表法与树状图法.
【分析】(1)根据所有等级的百分比的和为1,则可计算出x=30,再利用A等级的人数除以它所占的百分比得到调查的总人数为200人,然后分别乘以30%和20%得到B等级和C等级人数,再将条形统计图补充完整;
(2)满足2≤t<4的人数就是B和C等级的人数,用2500乘以B、C两等级所占的百分比的和即可;
(3)3人学习组的3个人用甲表示,2人学习组的2个人用乙表示,画树状图展示所有20种等可能的结果数,其中选出的2人来自不同小组占12种,然后利用概率公式求解.
【详解】解:(1)∵x%+15%+10%+45%=1,
∴x=30;
∵调查的总人数=90÷45%=200(人),
∴B等级人数=200×30%=60(人);C等级人数=200×10%=20(人),
如图:
(2)2500×(10%+30%)=1000(人),
所以估计每周课外阅读时间量满足2≤t<4的人数为1000人;
(3)3人学习组的3个人用甲表示,2人学习组的2个人用乙表示,画树状图为:
 ,
,
共有20种等可能的结果数,其中选出的2人来自不同小组占12种,
所以选出的2人来自不同小组的概率= =
= .
.

【点评】本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来;从条形图可以很容易看出数据的大小,便于比较.也考查了扇形统计图、列表法与树状图法.
五、(本大题共3小题,每题8分,共16分)
21.(7分)某工厂现有甲种原料280千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1200元.设生产A、B两种产品总利润为y元,其中A种产品生产件数是x.
(1)写出y与x之间的函数关系式;
(2)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
【考点】一次函数的应用.
【分析】(1)根据等量关系:利润=A种产品的利润+B中产品的利润,可得出函数关系式;
(2)这是一道只有一个函数关系式的求最值问题,可根据等量关系总利润═A种产品的利润+B中产品的利润,可得出函数关系式,然后根据函数的性质确定自变量的取值范围,由函数y随x的变化求出最大利润.
【详解】解:(1)y=700x+1200(50﹣x),
即y=﹣500x+60000;
(2)y=﹣500x+60000,
y随x的增大而减小,
当x=0时,y最大=60000,
生产B种产品50件,A种产品0件,总利润y有最大值,y最大=60000元.
【点评】本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.
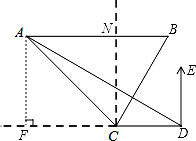
22.(8分)海中两个灯塔A、B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这是测得灯塔A在北偏西60°方向上,求灯塔A、B间的距离.(计算结果用根号表示,不取近似值)
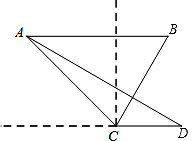
【考点】解直角三角形的应用-方向角问题.
【分析】根据方向角的定义以及锐角三角函数关系得出AN,NC的长进而求出BN即可得出答案.
【详解】解:如图所示:
由题意可得出:∠FCA=∠ACN=45°,∠NCB=30°,∠ADE=60°,
过点A作AF⊥FD,垂足为F,
则∠FAD=60°,∠FAC=∠FCA=45°,∠ADF=30°,
∴AF=FC=AN=NC,
设AF=FC=x,
∴tan30°= =
= =
= ,
,
解得:x=15(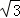 +1),
+1),
∵tan30°= ,∴
,∴ =
=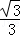 ,
,
解得:BN=15+5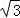 ,
,
∴AB=AN+BN=15(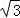 +1)+15+5
+1)+15+5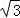 =30+20
=30+20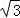 ,
,
答:灯塔A、B间的距离为(30+20 )海里.
)海里.
【点评】此题主要考查了方向角以及锐角三角函数关系,得出NC的长是解题关键.
23.(8分)已知x1,x2是关于x的一元二次方程x2﹣2(m+1)x+m2+5=0的两实数根.
(1)若(x1﹣1)(x2﹣1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
【考点】根与系数的关系;三角形三边关系;等腰三角形的性质.
【分析】(1)利用(x1﹣1)(x2﹣1)=x1•x2﹣(x1+x2)+1=m2+5﹣2(m+1)+1=28,求得m的值即可;
(2)分7为底边和7为腰两种情况分类讨论即可确定等腰三角形的周长.
【详解】解:(1)∵x1,x2是关于x的一元二次方程x2﹣2(m+1)x+m2+5=0的两实数根,
∴x1+x2=2(m+1),x1•x2=m2+5,
∴(x1﹣1)(x2﹣1)=x1•x2﹣(x1+x2)+1=m2+5﹣2(m+1)+1=28,
解得:m=﹣4或m=6;
当m=﹣4时原方程无解,
∴m=6;
(2)当7为底边时,此时方程x2﹣2(m+1)x+m2+5=0有两个相等的实数根,
∴△=4(m+1)2﹣4(m2+5)=0,
解得:m=2,
∴方程变为x2﹣6x+9=0,
解得:x1=x2=3,
∵3+3<7,
∴不能构成三角形;
当7为腰时,设x1=7,
代入方程得:49﹣14(m+1)+m2+5=0,
解得:m=10或4,
当m=10时方程变为x2﹣22x+105=0,
解得:x=7或15
∵7+7<15,不能组成三角形;
当m=4时方程变为x2﹣10x+21=0,
解得:x=3或7,
此时三角形的周长为7+7+3=17.
【点评】本题考查了根与系数的关系及三角形的三边关系,解题的关键是熟知两根之和和两根之积分别与系数的关系.
六、(本大题共2小题,每小题12分,共24分)
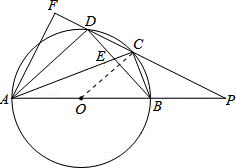
24.(12分)如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD=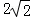 ,求DF的长.
,求DF的长.

【考点】相似三角形的判定与性质;勾股定理;圆周角定理.
【分析】
(1)求出△CDE∽△CAD,∠CDB=∠DBC得出结论.
(2)连接OC,先证AD∥OC,由平行线分线段成比例性质定理求得PC=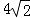 ,再由割线定理PC•PD=PB•PA求得半径为4,根据勾股定理求得AC=
,再由割线定理PC•PD=PB•PA求得半径为4,根据勾股定理求得AC=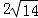 ,再证明△AFD∽△ACB,得
,再证明△AFD∽△ACB,得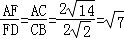 ,则可设FD=x,AF=
,则可设FD=x,AF= ,在Rt△AFP中,求得DF=
,在Rt△AFP中,求得DF=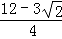 .
.
【详解】(1)证明:∵DC2=CE•CA,
∴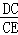 =
= ,
,
△CDE∽△CAD,
∴∠CDB=∠DBC,
∵四边形ABCD内接于⊙O,
∴BC=CD;
(2)解:如图,连接OC,
∵BC=CD,
∴∠DAC=∠CAB,
又∵AO=CO,
∴∠CAB=∠ACO,
∴∠DAC=∠ACO,
∴AD∥OC,
∴ =
=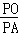 ,
,
∵PB=OB,CD=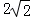 ,
,
∴ =
=
∴PC=4
又∵PC•PD=PB•PA
∴PA=4也就是半径OB=4,
在RT△ACB中,
AC=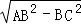 =
=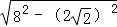 =2
=2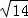 ,
,
∵AB是直径,
∴∠ADB=∠ACB=90°
∴∠FDA+∠BDC=90°
∠CBA+∠CAB=90°
∵∠BDC=∠CAB
∴∠FDA=∠CBA
又∵∠AFD=∠ACB=90°
∴△AFD∽△ACB
∴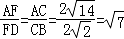
在Rt△AFP中,设FD=x,则AF= ,
,
∴在RT△APF中有, ,
,
求得DF=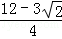 .
.
【点评】本题主要考查相似三角形的判定及性质,勾股定理及圆周角的有关知识的综合运用能力,关键是找准对应的角和边求解.
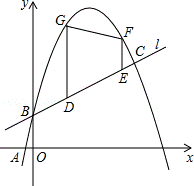
25.(12分)如图,已知一次函数y1= x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣
x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣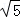 ,0).
,0).
(1)求二次函数的最大值;
(2)设使y2>y1成立的x取值的所有整数和为s,若s是关于x的方程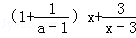 =0的根,求a的值;
=0的根,求a的值;
(3)若点F、G在图象C′上,长度为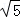 的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
【考点】二次函数综合题.
【分析】(1)首先利用待定系数法求出二次函数解析式,然后求出其最大值;
(2)联立y1与y2得,求出点C的坐标为C(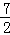 ,
,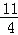 ),因此使y2>y1成立的x的取值范围为0<x<
),因此使y2>y1成立的x的取值范围为0<x<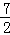 ,得s=1+2+3=6;将s的值代入分式方程,求出a的值;
,得s=1+2+3=6;将s的值代入分式方程,求出a的值;
(3)第1步:首先确定何时四边形DEFG的面积最大.
如答图1,四边形DEFG是一个梯形,将其面积用含有未知数的代数式表示出来,这个代数式是一个二次函数,根据其最值求出未知数的值,进而得到面积最大时点D、E的坐标;
第2步:利用几何性质确定PD+PE最小的条件,并求出点P的坐标.
如答图2,作点D关于x轴的对称点D′,连接D′E,与x轴交于点P.根据轴对称及两点之间线段最短可知,此时PD+PE最小.利用待定系数法求出直线D′E的解析式,进而求出点P的坐标.
【详解】解:(1)∵二次函数y2=﹣x2+mx+b经过点B(0,1)与A(2﹣ ,0),
,0),
∴ ,
,
解得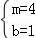
∴l:y1= x+1;
x+1;
C′:y2=﹣x2+4x+1.
y2=﹣x2+4x+1=﹣(x﹣2)2+5,
∴ymax=5;
(2)联立y1与y2得: x+1=﹣x2+4x+1,解得x=0或x=
x+1=﹣x2+4x+1,解得x=0或x= ,
,
当x= 时,y1=
时,y1= ×
× +1=
+1= ,
,
∴C(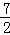 ,
, ).
).
使y2>y1成立的x的取值范围为0<x<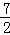 ,
,
∴s=1+2+3=6.
代入方程得
解得a=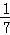 ;
;
(3)∵点D、E在直线l:y1=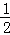 x+1上,
x+1上,
∴设D(p,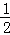 p+1),E(q,
p+1),E(q,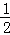 q+1),其中q>p>0.
q+1),其中q>p>0.
如答图1,过点E作EH⊥DG于点H,则EH=q﹣p,DH=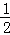 (q﹣p).
(q﹣p).
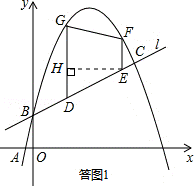
在Rt△DEH中,由勾股定理得:DE2+DH2=DE2,即(q﹣p)2+[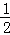 (q﹣p)]2=(
(q﹣p)]2=(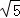 )2,
)2,
解得q﹣p=2,即q=p+2.
∴EH=2,E(p+2, p+2).
p+2).
当x=p时,y2=﹣p2+4p+1,
∴G(p,﹣p2+4p+1),
∴DG=(﹣p2+4p+1)﹣( p+1)=﹣p2+
p+1)=﹣p2+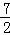 p;
p;
当x=p+2时,y2=﹣(p+2)2+4(p+2)+1=﹣p2+5,
∴F(p+2,﹣p2+5)
∴EF=(﹣p2+5)﹣( p+2)=﹣p2﹣
p+2)=﹣p2﹣ p+3.
p+3.
S四边形DEFG= (DG+EF)•EH=
(DG+EF)•EH= [(﹣p2+
[(﹣p2+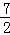 p)+(﹣p2﹣
p)+(﹣p2﹣ p+3)]×2=﹣2p2+3p+3
p+3)]×2=﹣2p2+3p+3
 则有
则有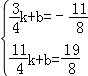 ,
,
解得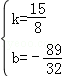
∴直线D′E的解析式为:y= x﹣
x﹣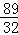 .
.
令y=0,得x=89/60,
∴P(89/60,0).
【点评】本题是二次函数压轴题,综合考查了二次函数与一次函数的图象与性质、待定系数法、函数最值、分式方程的解、勾股定理、轴对称﹣最短路线等知识点,涉及考点众多,难度较大.本题难点在于第(3)问,涉及两个最值问题,第1个最值问题利用二次函数解决,第2个最值问题利用几何性质解决.


