(单词翻译:单击)
一、选择题
1. 的倒数是( )
的倒数是( )
A.2 B.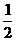 C.
C.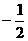 D.
D.
2.下列电视台的台标,是中心对称图形的是( )




A. B. C. D.
3.若 ,则下列式子中错误的是( )
,则下列式子中错误的是( )
A. B.
B.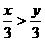 C.
C.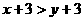 D.
D.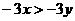
4.在我国南海某海域探明可燃冰储量约有194亿立方米.数字19 400 000 000用科学记数法表示正确的是( )
A. B.
B.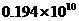 C.
C.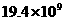 D.
D.

5.下列各式计算正确的是( )
A.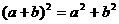 B.
B.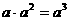
C.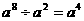 D.
D.
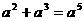
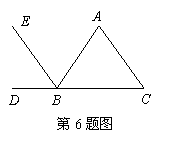
6.如图,能判定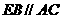 的条件是( )
的条件是( )
A.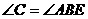 B.
B.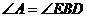
C. D.
D.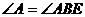
7.在Rt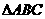 中,
中,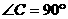 ,若
,若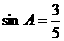 ,则
,则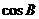 的值是( )
的值是( )
A.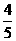
 B.
B.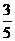 C.
C.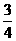 D.
D.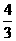
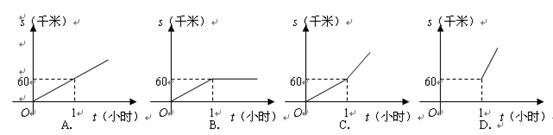
8.汽车以60千米/时的速度在公路上匀速行驶,1小时后进入高速路,继续以100千米/时的速度匀速行驶,则汽车行驶的路程s(千米)与行驶的时间t(时)的函数关系的大致图象是( )
9.如图是一个正方体展开图,把展开图折叠成正方体后,“你”字一面相对面上的字是( )

A.我 B.中
C.国 D.梦
10.已知直线 ,若
,若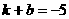 ,
,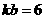 ,那么该直线不经过( )
,那么该直线不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
11.4的平方根是___________
12.已知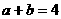 ,
,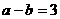 ,则
,则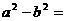 ___________
___________
13.已知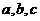 为平面内三条不同直线,若
为平面内三条不同直线,若 ,
,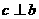 ,则
,则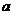 与
与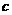 的位置关系是 ___________
的位置关系是 ___________
14.小明在射击训练中,五次命中的环数分别为5,7,6,6,6,则小明命中环数的众数为
__________,平均数为 ___________
15.写出一个在三视图中俯视图与主视图完全相同的几何体___________
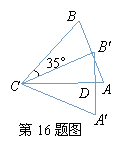
16.如图,把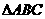 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转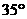 ,得到
,得到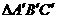 ,
,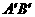 交
交 于点D,若
于点D,若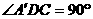 ,则
,则 ___________ °.
___________ °.
三、解答题
17.计算: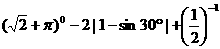 .
.
18.已知反比例函数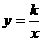 的图象经过点M(2,1).
的图象经过点M(2,1).
(1)求该函数的表达式;
(2)当 时,求
时,求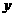 的取值范围.(直接写出结果)
的取值范围.(直接写出结果)
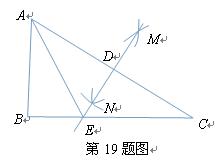
19.如图,在Rt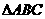 中,
中,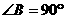 ,分别以点A、C为圆心,大于
,分别以点A、C为圆心,大于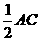 长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.
长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.
(1)求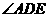 ;(直接写出结果)
;(直接写出结果)
(2)当AB=3,AC=5时,求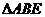 的周长.
的周长.
四、解答题
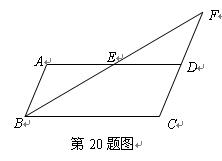
20、如图,在平行四边形ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线 于点F.
于点F.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.
21.一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3.从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
22.已知关于x的方程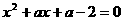 .
.
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
五、解答题
23.某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲 、乙两工程队每天能完成绿化的面积分别是多少m2?
、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
24.如图,在Rt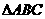 中,
中,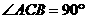 ,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证: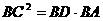 ;
;
(3)当以点O、D、E、C为顶点的四边形是正方形时,
求证:△ABC是等 腰直角三角形.
腰直角三角形.

25.如图,已知抛物线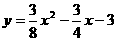 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.

2014年广东省 汕尾市中考数学试卷参考答案
汕尾市中考数学试卷参考答案
一、选择题(共10小题,每小题4分,共40分)
1. C.
2.A
3.D
4.A
5.B
6.D
7.B
8.C
9.D
10.A
二、填空题(共6小题,每小题5分,共30分)
11.±2.
12. 12.
13.平行.
14. 6,6.
15.球或正方体.
16.55°.
三、解答题(一)(共3小题,每小题7分,共21分)
17.解 :原式=1﹣2×
:原式=1﹣2×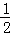 +2=1﹣1+2=2.
+2=1﹣1+2=2.
18.解:(1)∵反比例函数y=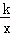 的图象经过点M(2,1),∴k=2×1=2,
的图象经过点M(2,1),∴k=2×1=2,
∴该函数的表达式为y=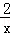 ;
;
(2)∵y=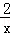 ,∴x=
,∴x=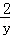 ,∵2<x<4,∴2<
,∵2<x<4,∴2<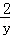 <4,解得:
<4,解得: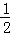 <y<1.
<y<1.
19.解:(1)∵由题意可知MN是线段AC的垂直平分线,∴∠ADE=90°;
(2)∵在Rt△ABC中,∠B=90°,AB=3,AC=5,∴BC=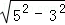 =4,
=4,
∵MN是线段AC的垂直平分线,∴AE=CE,
∴△ABE的周长=AB+(AE+BE)=AB+BC=3+4=7.
四、解答题(二)(共3小题,每小题9分,共27分)
20.(1)证明:∵在平行四边形ABCD中,E是AD边上的中点,∴AE=ED,∠ABE=∠F,
在△ABE和△DFE中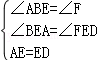 ,∴△ABE≌△DFE(AAS),∴FD=AB;
,∴△ABE≌△DFE(AAS),∴FD=AB;
(2)解:∵DE∥BC,∴△FED∽△FBC,∵△ABE≌△DFE,
 ∴BE=EF,S△FDE=S平行四边形ABCD,∴
∴BE=EF,S△FDE=S平行四边形ABCD,∴ =
=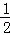 ,∴
,∴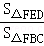 =
=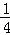 ,∴
,∴ =
=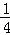 ,
,
∴△FED的面积为:2.
21.解:(1)画树状图得:
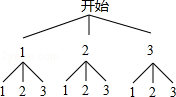
则共有9种等可能的结果;
(2)由(1)得:两次摸出的球上的数字和为偶数的有5种情况,
∴两次摸出的球上的数字和为偶数的概率为: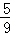 .
.
22.解:(1)将x=1代入方程x2+ax+a﹣2=0得,1+a+a﹣2=0,解得,a=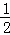 ;
;
方程为x2+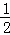 x﹣
x﹣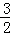 =0,即2x2+
=0,即2x2+ x﹣3=0,设另一根为x1,则1x1=﹣
x﹣3=0,设另一根为x1,则1x1=﹣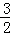 ,x1=﹣
,x1=﹣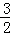 .
.
(2)∵△=a2﹣4(a﹣2)=a2﹣4a+8=a2﹣4a+4+4=(a﹣2)2+4≥0,
∴不论a取何实数,该方程都有两个不相等的实数根.
点评:本题考查了根的判别式和根与系数的关系,要记牢公式,灵活运用.
五、解答题(三)(共3小题,第23、24小题各11分,第25小题10分,共32分)
23.解:(1)设乙工程队每天能完成绿化的面积是xm2,根据题意得: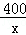 ﹣
﹣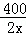 =4,
=4,
解得:x=50经检验x=50是原方程的解,
则甲工程队每天能完成绿化的面积是50×2=100(m2),
答:甲、乙两工程队每天能完成绿化的面积分别是100m2、50m2;
(2)设至少应安排甲队工作x天,根据题意得:
0.4x+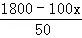 ×0.25≤8,解得:x≥10,
×0.25≤8,解得:x≥10,
答:至少应安排甲队工作10天 .
.
24.证明:(1)如图,连接OD .∵DE为切线,∴∠EDC+∠ODC=90°;
.∵DE为切线,∴∠EDC+∠ODC=90°;
∵∠ACB=90°,∴∠ECD+∠OCD=90°.又∵OD=OC,∴∠ODC=∠OCD,
∴∠EDC=∠ECD,∴ED=EC;∵AC为直径,∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,∴∠B=∠BDE,∴ED=DB.
∴EB=EC,即点E为边BC的中点;
(2)∵AC为直径,∴∠ADC=∠ACB=90°,又∵∠B=∠B
∴△ABC∽△CDB,∴ ,∴BC2=BD•BA;
,∴BC2=BD•BA;
(3)当四边形ODEC为正方形时,∠OCD=45°;∵AC为直径,
∴∠ADC=90°,∴∠CAD=∠ADC﹣∠OCD=90°﹣45°=45°
∴Rt△ABC为等腰直角三角形.
点评:本题是几何证明题,综合考查了切线性质、圆周角定理、相似三角形、正方形、等腰直角三角形等知识点.试题着重对基础知识的考查,难度不大.
25.解:(1)∵y=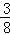 x2﹣
x2﹣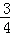 x﹣3,∴当y=0时,
x﹣3,∴当y=0时,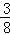 x2﹣
x2﹣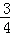 x﹣3=0,
x﹣3=0,
解得x1=﹣2,x2=4.当x=0,y=﹣3.
∴A点坐标为(4,0),D点坐标为(﹣2,0),C点坐标为(0,﹣3);
(2)∵y=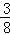 x2﹣
x2﹣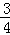 x﹣3,∴对称轴为直线x=
x﹣3,∴对称轴为直线x= =1.
=1.
∵AD在x轴上,点M在抛物线上,
∴当△MAD的面积与△CAD的面积相等时,分两种情况:
①点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,
∵C点坐标为(0,﹣3),∴M点坐标为(2,﹣3);
②点M在x轴上方时,根据三角形的等面积法,可知M点到x轴的距离等于点C到x轴的距离3.当y=4时,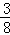 x2﹣
x2﹣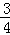 x﹣3=3,解得x1=1+
x﹣3=3,解得x1=1+ ,x2=1﹣
,x2=1﹣ ,
,
∴M点坐标为(1+ ,3)或(1﹣
,3)或(1﹣ ,3).
,3).
综上所述,所求M点坐标为(2,﹣3)或(1+ ,3)或(1﹣
,3)或(1﹣ ,3);
,3);
(3)结论:存在.
如图所示,在抛物线上有两个点P满足题意:
①若BC∥AP1,此时梯形为ABCP1.
由点C关于抛物线对称轴的对称点为B,可知BC∥x轴,则P1与D点重合,
∴P1(﹣2,0).∵P1 A=6,BC=2,∴P1A≠BC,∴四边形ABCP1为梯形;
A=6,BC=2,∴P1A≠BC,∴四边形ABCP1为梯形;
②若AB∥CP2,此时梯形为ABCP2.
∵A点坐标为(4,0),B点坐标为(2,﹣3),∴直线AB的解析式为y=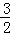 x﹣6,
x﹣6,
∴可设直线CP2的解析式为y=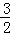 x+n,将C点坐标(0,﹣3)代入,得b=﹣3,
x+n,将C点坐标(0,﹣3)代入,得b=﹣3,
∴直线CP2的解析式为y=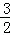 x﹣3.∵点P2在抛物线y=
x﹣3.∵点P2在抛物线y=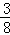 x2﹣
x2﹣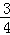 x﹣3上,
x﹣3上,
∴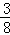 x2﹣
x2﹣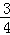 x﹣3=
x﹣3=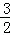 x
x ﹣3,化简得:x2﹣6x=0,解得x1=0(舍去),x2=6,
﹣3,化简得:x2﹣6x=0,解得x1=0(舍去),x2=6,
∴点P2横坐标为6,代入直线CP2解析式求得纵坐标为6,∴P2(6,6).
∵AB∥CP2,AB≠CP2,∴四边形ABCP2为梯形.
综上所述,在抛物 线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(﹣2,0)或(6,6).
线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(﹣2,0)或(6,6).


