每日一题

Mathematics>Standard Multiple Choice

Read the following SAT test question and then click on a button to select your answer.

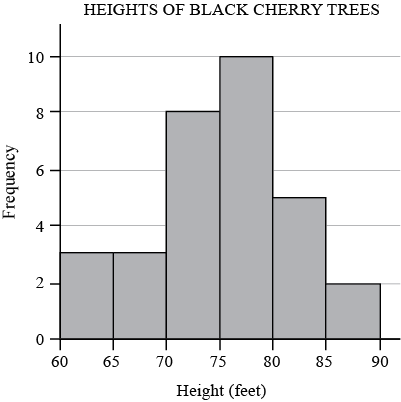
The histogram above shows the distribution of 31 black cherry trees, by height. For example, the leftmost bar represents the black cherry trees that are at least 60 feet, but less than 65 feet, in height. Based on the histogram, which of the following can be the average (arithmetic mean) height of the 31 black cherry trees?

(A) 70 feet
(B) 72 feet
(C) 74 feet
(D) 78 feet
(E) 80 feet

答案和解析

答案：C

解析：

The histogram does not give the recorded heights for each cherry tree, but rather the intervals in which the heights lie. Thus, to find possible values for the average (arithmetic mean) height, one can find lower and upper bounds for the average height by calculating the averages of lower and upper interval bounds of the histogram with the frequencies given. A lower bound for the average, found by using the value at the left endpoint of the interval, is ((60*3) + (65*3) + (70*8) + (75*10) + (80*5) + (85*2)) over 31 is approximately equal to 72.74 feet, and so 72.74 + 5 = 77.74 feet would be an upper bound for the average height. Therefore, the average height of the 31 black cherry trees can be between 72.74 feet and 77.74 feet. Of the choices given, only 74 feet can be a possible value for the average height of the 31 black cherry trees.