(单词翻译:单击)
数学模拟题
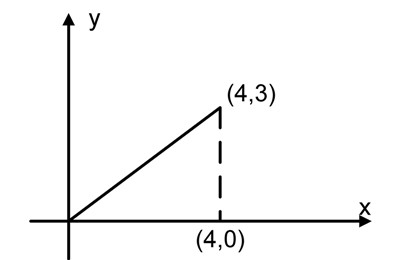
Question 1: In the x,y plane, what is the distance between origin and the (4,3) point?
Question 2: The sum of 4 consecutive integers is 26. What is the product of the 4 numbers?
Question 3: 60% of the players of a team score 5 points each during a basketball game, 30% of players score 1 point each, and 10% score 7 points each. What is the average number of points scored by the players of the team?
Question 4: If f(x) = x - 1, what is the value of x that satisfies the equality f(x) - 1 = f(x2) - x2
Question 5: The amount of time taken to build a house is inversely proportional to the number of construction workers on the job. If it takes 6 workers 6 days to complete such a job, how many days will it take if the job is done by only 4 workers?
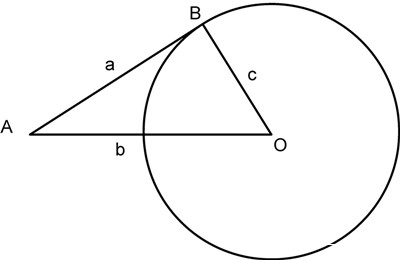
Question 6: If side a of triangle ABO is tangent to the circle of center O, what is the value of the radius of the circle in inches? Side a of the ABO triangle is 4 inches and side b of the same triangle is 5 inches.
Question 7: A jar contains a nickel, a dime, and six quarters. Tom draws a coin from the jar, and then Mary draws a coin from those remaining. If the probability that Tom draws the nickel and Mary draws the dime is 1/x, what is the value of x?
Question 8: What is the length of the sides of an equilateral triangle, if the lengths of the altitudes of the triangle are √3?
Question 9: If the population of virus doubles every 90 minutes, the population after 9 hours will be how many times the population at the start?
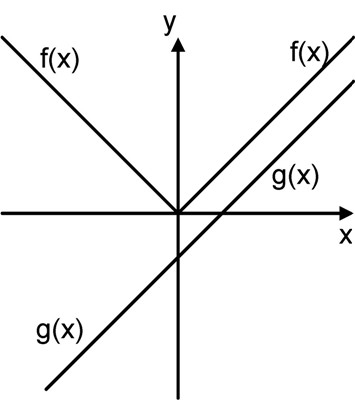
Question 10: f(x) = |x| and g(x) = x - 1. How many solutions x satisfy f(x) = g(x)?
参答案
参考答案:
SAT考试Grid-in数学习题参考答案
Question 1: In the x,y plane, what is the distance between origin and the (4,3) point?
Answer: 5
Explanation: We apply Pythagoras' Theorem to the triangle created by the following points: (4,3), (4,0) and (0,0).
The distance between origin and the (4,3) point is equal to 5, as the other 2 sides of this right triangle are 4 and 3.
Question 2: The sum of 4 consecutive integers is 26. What is the product of the 4 numbers?
Answer: 1680
Explanation: If m is the least of the integers, m + (m + 1) + (m + 2) + (m + 3) = 26
4m + 6 = 26
m = 5, so the 4 consecutive numbers are 5, 6, 7, 8.
Their product is 5·6·7·8 = 1680
Question 3: 60% of the players of a team score 5 points each during a basketball game, 30% of players score 1 point each, and 10% score 7 points each. What is the average number of points scored by the players of the team?
Answer: 4
Explanation: n being the number of players, 60% of the players is .6·n, 30% of the players is .3·n and 10% of the players is .1·n.
The numbers of points scored by players that scored 5 points is (.6·n)·5.
The numbers of points scored by players that scored 1 point is (.3·n)·1.
The numbers of points scored by players that scored 7 points is (.1·n)·7.
The total number of points will be (.6·n)·5 + (.3·n)·1 + (.1·n)·7 = 4·n and the average number of points = ( total number of points)/number of players = 4·n/n = 4
Question 4: If f(x) = x - 1, what is the value of x that satisfies the equality f(x) - 1 = f(x2) - x2
Answer: 1
Explanation:
f(x) - 1 = f(x2) - x2
(x - 1) - 1 = (x - 1)2 - x2
x - 2 = x2 - 2x + 1 - x2
x - 2 = -2x + 1
x = 1
Question 5: The amount of time taken to build a house is inversely proportional to the number of construction workers on the job. If it takes 6 workers 6 days to complete such a job, how many days will it take if the job is done by only 4 workers?
Answer: 9
Explanation: The amount of time taken to build a house is inversely proportional to the number of construction workers on the job, so Nworkers = k/Ndays
k = Nworkers·Ndays
k = 6·6, as it takes 6 workers 6 days to build the house
k = 36 worker·days
k = 4 workers · Ndays_4workers
Ndays_4workers = 36/4 = 9 days
Question 6: If side a of triangle ABO is tangent to the circle of center O, what is the value of the radius of the circle in inches? Side a of the ABO triangle is 4 inches and side b of the same triangle is 5 inches.

Answer: 3
Explanation: Side a is tangent to the circle, so the triangle created by the sides a, b and c is right.
c2 = b2 - a2
c2 = 52 - 42
c2 = 9
c = 3
Question 7: A jar contains a nickel, a dime, and six quarters. Tom draws a nickel from the jar, and then Mary draws a dime from those remaining. If the probability that Tom draws the nickel and Mary draws the dime is 1/x, what is the value of x?
Answer: 56
Explanation: The probability that Tom draws the nickel is (number of nickels)/(number of coins in the jar) = 1/8
After Tom draws a coin, the number of coins in the jar is 8 - 1 = 7
The probability that Mary draws the dime is (number of dimes)/(number of coins in the jar) = 1/7
The probability that Tom draws the nickel AND Mary draws the dime is the product of the 2 probabilities calculated above.
1/8 · 1/7 = 1/56 so x = 56
Question 8: What is the length of the sides of an equilateral triangle, if the lengths of the altitudes of the triangle are √3?
Answer: 2
Explanation: In the triangle formed by the the altitude a, one side l and the base of the altitude, l2 = a2 + (l/2)2
(3/4)·l2 = a2
(3/4)·l2 = (√3)2
(3/4)·l2 = 3
l2 = 4 and l = 2.
Question 9: If the population of virus doubles every 90 minutes, the population after 9 hours will be how many times the population at the start?
Answer: 64
Explanation:
After 90 minutes the virus population will be 2·x, where x is the population at the start.
After 3 hours the virus population will be 2·(2·x) = 22·x.
After 4 hours and 30 minutes, the population will be 23·x.
After 6 hours, the population will be 24·x.
After 7 hours and 30 minutes, the population will be 25·x.
After 9 hours, the population will be 26·x.
Question 10: f(x) = |x| and g(x) = x - 1. How many solutions x satisfy f(x) = g(x)?
Answer: 0
Explanation:
The simplest way to solve this problem is to draw the 2 functions in the x,y plane.
We notice that for any x < 0, f(x) is positive and g(x) is negative and they don't intersect.
For any x > 0, f(x) is parallel with g(x) and they do not intersect
in conclusion there are no x that satisfy f(x) = g(x).