(单词翻译:单击)
一、选择题(本大题共12小题,每小题3分,满分36分;在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案号涂黑).
1.计算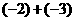 的结果是
的结果是
A.-5 B.-1 C.1 D.5
2.从上往下看如图所示的几 何体,得到的图形是
何体,得到的图形是
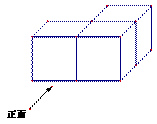

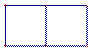
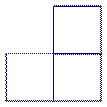
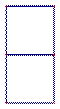
A. B. C. D.
3.甲、乙、丙、丁四人参加射击训练,每人各射击20次,他们射击成绩的平均数是9.1环,各自的方差见如下表格:
甲 | 乙 | 丙 | 丁 | |
方差 | 0.293 | 0.375 | 0.362 | 0.398 |
由上可知射击成绩最稳定的是
A. 甲 B.乙 C.丙 D.丁
甲 B.乙 C.丙 D.丁
4.已知两圆的半径分别为1cm和4cm,圆心距为5cm,那么这两个圆的位置关系是
A.内切 B.相交 C.外切 D.外离
5.在平面直角坐标系中,点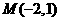 在
在
A.第一象限 B.第二象限 C.第三象限  D.第四象限
D.第四象限
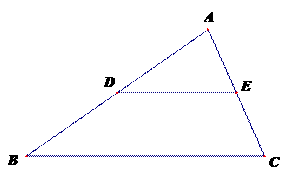
6.如图,在△ABC中,D、E分别是边AB、AC的中点,已知DE=5,则BC的长为
A.8 B.9 C.10 D.11
7.下列几何图形中,一定是轴对称图形的有

A.1个 B.2个 C.3个 D.4个
8.下列命题中,不正确的是
A.n边形的内角和等于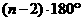
B.两组对边分别相等的四边形是矩形
C.垂直于弦的直径平分弦所对的两条弧
D.直角三角形斜边上的中线等于斜边的一半
9.已知一个扇形的半径为12,圆心角为150°,则此扇形的弧长是
A.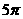 B.
B.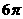 C.
C.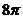 D.
D.
10.北海到南宁的铁路长210千米,动车运行后的平均速度是原来火车的1.8倍,这样由北海到南宁的行驶时间缩短了1.5小时,设原来火车的平均速度为x千米/时,则下列方程正确的是
A.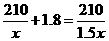 B.
B.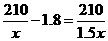
C.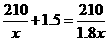 D.
D.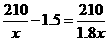
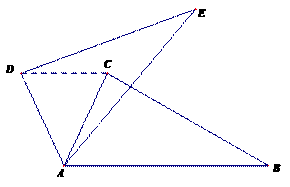
11.如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC ∥AB,则∠BAE等于
∥AB,则∠BAE等于
A.30° B.40° C.50° D.60°
12.函数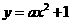 与
与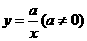 在同一平面直角坐标系中的图象可能是
在同一平面直角坐标系中的图象可能是
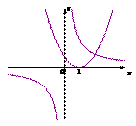
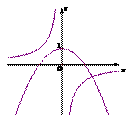

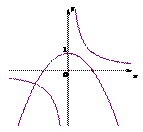
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,满分18分,请将答案填在答题卡上)
13.已知∠A=43°,则∠A的补角等于_________度.
14.因式分解: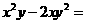 _______.
_______.
15.若一元二次方程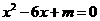 有两个相等的实数根,则m的值为_______.
有两个相等的实数根,则m的值为_______.
16.某校男子足球队的年龄分布如下面的条形统计图所示,则这些足球队员的年龄的中位数是_______岁.
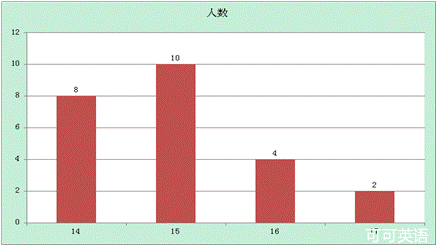

17.下列式子按一定规律排列: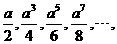 则第2014个式子是_______ .
则第2014个式子是_______ .
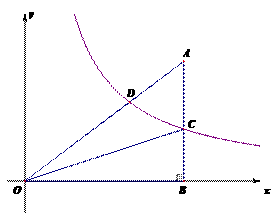
18.如图,反比例函数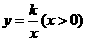 的图象交Rt△AOB的斜边OA于点D,交直角边AB于点C,点B在x轴上.若△OAC的面积为5,
的图象交Rt△AOB的斜边OA于点D,交直角边AB于点C,点B在x轴上.若△OAC的面积为5,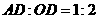 ,则k的值为 _______.
,则k的值为 _______.
三、解答题(本大题共8小题,满分66分.请在答题卡上答题,解答应写出必要的文字说明、演算步骤或推理过程)
19.(本题满分6分)计算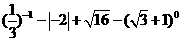
20.(本题满分6分)解方程组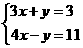
21.(本题满分8分)经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同.现有两辆汽车经过这个十字路口,
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率.
22.(本题满分8分)已知△ABC中,∠A=25°,∠B=40°.
(1)求作:,使得⊙O经过A、C两点,且圆心O落在AB边上.(要求尺规作图,保留作图痕迹,不必写作法)
(2)求证:BC是(1)中所作⊙O的切线.

23.(本题满分8分)下图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(保留小数点后两位;参考数据:sin22°=0.3746,cos22°=0.9272,tan22°=0.4040)

24.(本题满分8分)某经销商从市场得知如下信息
A品牌手表 | B品牌手表 | |
进价(元/块) | 700 | 100 |
售价(元/块) | 900 | 160 |
他计划用4万元的资金一次性购进这两种品牌手表共100块.设该经销商购进A品牌手表x块,这两种品牌手表全部 销售完后获得的利润为y元.
销售完后获得的利润为y元.
(1)试写出y与x之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案?
(3)选择哪种进货方案,该经销商可获利最大?最大利润是多少元?
25.(本题满分10分)如图(1),E是正方形ABCD的边BC上的一个点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.
(1)求证:FG=BE;
(2)连接CF,如图(2),求证:CF平分∠DCG;
(3)当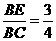 ,求sin∠CFE的值.
,求sin∠CFE的值.


(1) (2)
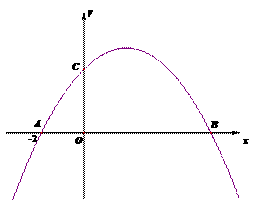
26.(本题满分12分)如图(1)抛物线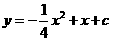 与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为
与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为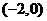 .
.
(1)求此抛物线的解析式;
(2)①若点D是第一象限内抛物线上的一个动点,过点D作DE⊥x轴于E,连接CD,以OE为直径作⊙M,如图(2)试求当CD与⊙M相切时D点的坐标;
②点F是x轴上的动点,在抛物线上是否存在一点G,使以A、C、G 、F四点为顶点的四边形是平行四边形?若存在,求存点G的坐标;若不存在,请说明理由.
、F四点为顶点的四边形是平行四边形?若存在,求存点G的坐标;若不存在,请说明理由.

一、选择题
1. A;2.C ;3.A;4. C;5.B ;6.C ;7.D ;8.B ;9.D ;10.D ;11.C ;12. B。
二、填空题
13、137°;14、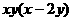 ;15、9;16、10;17、
;15、9;16、10;17、
 ;18、8
;18、8
三、解答题
19. 解:原式=3-4+2-1=0
20. 解:①+②得7x=14, ∴x=2,把x=2代入①得6+y=3, ∴y= -3
∴原方程组的解是: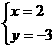
21. 解:(1)两辆 汽车所有9种可能的行驶方向如下:
汽车所有9种可能的行驶方向如下:
甲汽车 乙汽车 | 左转 | 右转 | 直行 |
左转 | (左转,左转) | (右转,左转) | (直行,左转) |
右转 | (左转,右转) | (右转,右转) | (直行,右转) |
直行 | (左转,直行) | (右转,直行 | (直行,直行) |

(2)由上表知:两辆汽车都向左转的概率是: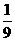 。
。
22. 解:(1)作图如右图1:
(2)如图2,连OC,∵OA=OC,∠A=25°
∴∠AOC=50°,

又∵∠C=40,
∴∠AOC+∠C=90°
∴∠OCB=90°
∴OC⊥BC
∴BC是⊙O的切线。
23. 解:由已 知有:∠BAE=22°,∠ABC=90°,∠CED=∠AEC=90°
知有:∠BAE=22°,∠ABC=90°,∠CED=∠AEC=90°
∴∠BCE=158°,∴∠DCE=22°,又∵tan∠BAE=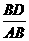 ,∴BD=A
,∴BD=A B·tan∠BAE,
B·tan∠BAE,
又∵cos∠BAE=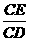 ,
,
∴CE= CD·cos∠BAE = (BD-BC) ·cos∠BAE= ( AB·tan∠BAE-BC) ·cos∠BAE
( AB·tan∠BAE-BC) ·cos∠BAE
=( 10×0.4040-0.5) ×0.9272≈3.28(m)
10×0.4040-0.5) ×0.9272≈3.28(m)
24.解:(1) y = 140x+6000,(x≤50)
y = 140x+6000,(x≤50)
(2)令y≥12600,则140x+6000≥12600,∴x≥47.1,又∵x≤50
∴经销商有以下三种进货方案:
方案 | A品牌(块) | B品牌(块) |
① | 48 | 52 |
| 49 | 51 |
③ | 50 |
|
(3)∵140>0,∴y随x的增大而增大,∴x=50时y取得最大值,
又∵140×50+6000=13000
∴选择方案③进货时,经销商可获利最大,最大利润是13000元。
25. 解:(1) 证明:
证明: ∵EP⊥AE,∴∠AEB+∠GEF=90°,又∵∠AEB+∠BAE=90°,∴∠GEF=∠BA
∵EP⊥AE,∴∠AEB+∠GEF=90°,又∵∠AEB+∠BAE=90°,∴∠GEF=∠BA E,又∵FG⊥BC,∴∠ABE=∠EGF=90°,在△ABE与△EGF中,
E,又∵FG⊥BC,∴∠ABE=∠EGF=90°,在△ABE与△EGF中,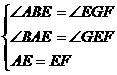 ,
,
∴△ABE≌△EGF,∴FG=BE
(2)由(1)知:BC=AB=EG,∴ BC-EC=EG-EC,∴BE=CG,又∵FG=BE,∴FG=CG,
BC-EC=EG-EC,∴BE=CG,又∵FG=BE,∴FG=CG,
又∵∠ CGF=90°,∴∠FCG=45°=
CGF=90°,∴∠FCG=45°=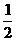 ∠DCG,∴CF平分∠DCG。
∠DCG,∴CF平分∠DCG。
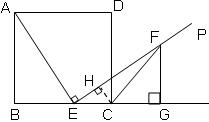 (3)如图,作CH⊥EF于H,则△EHC∽△EGF,∴
(3)如图,作CH⊥EF于H,则△EHC∽△EGF,∴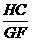 =
=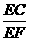
 ∵
∵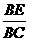 =
=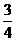 ,令BE=3a,则EC=3a,EG=4a,FG=CG=3a,
,令BE=3a,则EC=3a,EG=4a,FG=CG=3a,
∴EF=5a,CF=3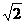 a,∴
a,∴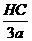 =
=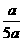 ,HC=
,HC=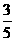 a,
a,
∴sin∠CFE=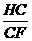 =
=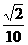

26. 解:(1)由已知有:-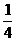
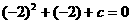 ,∴c=3,抛物线的解析式是:
,∴c=3,抛物线的解析式是: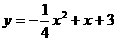 (2)①令D(x,y),(x>0,y>0),
(2)①令D(x,y),(x>0,y>0),
则E(x,0),M(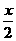 ,0),由(1)知C(0,3),
,0),由(1)知C(0,3),
连接MC、MD ∵DE、CD与⊙O相切,∴∠CMD=90°,
∵DE、CD与⊙O相切,∴∠CMD=90°,
∴△COM∽△MED,∴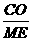 =
=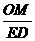 ,∴
,∴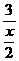 =
=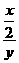 ,又∵
,又∵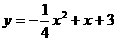 ,∴x=
,∴x=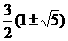 ,
,
又∵x>0,∴x=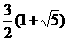 ,∴
,∴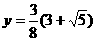 ,D点的坐标是:(
,D点的坐标是:(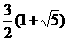 ,
,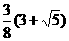 )。
)。
②假设存在满足条件的点G(a,b).
若构成的四边形是□ACGF,(下图1)则G与C关于直线x=2对称,∴G点的坐标是:(4,3);
若构成的四边形是□ACFG,(下图2)则由平行四边形的性质有b=-3,
又∵-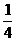
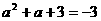
 ,∴a=2±2
,∴a=2±2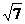 ,此时G点
,此时G点 的坐标是:(2±2
的坐标是:(2±2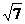 ,-3)
,-3)

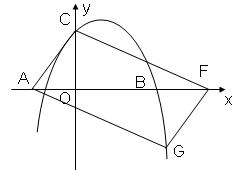
图1 图2


