(单词翻译:单击)
第Ⅰ卷(选择题,共24分)
一、选择题(每小题3分,共24分)
1. ﹣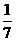 的相反数是( )
的相反数是( )
A.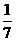 B. ﹣
B. ﹣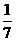 C. 7 D. ﹣7
C. 7 D. ﹣7

2. 下列图形中,是正方体表面展开图的是( )
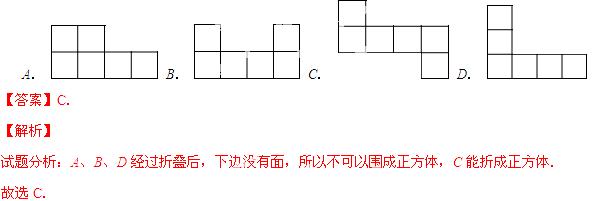
考点:几何体的展开图.
3. 计算(3ab)2的结果是( )
A. 6ab B. 6a2b C. 9ab2 D. 9a2b2

4. 不等式组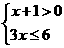 的解集为( )
的解集为( )
A. x≤2 B. x>﹣1 C. ﹣1<x≤2 D. ﹣1≤x≤2
B. x>﹣1 C. ﹣1<x≤2 D. ﹣1≤x≤2

考点:解一元一次不等式组.
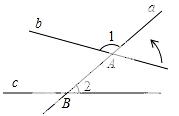
5. 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A. 15 ° B. 30° C. 45° D. 60°
° B. 30° C. 45° D. 60°
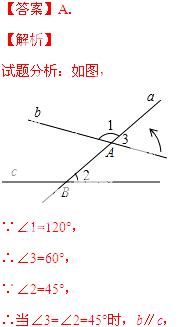
∴直线b绕点A逆时针旋转60°﹣45°=15°.
故选A.
考点:平行线的判定.
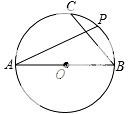
6. 如图,在⊙O中,AB是直径,BC是弦,点P是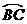 上任意一点.若AB=5,BC=3,则AP的长不可能为( )
上任意一点.若AB=5,BC=3,则AP的长不可能为( )
A. 3 B. 4 C.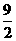 D. 5
D. 5
【答案】A.
【解析】

考点:1.圆周角定理2.勾股定理2.圆心角、弧、弦的关系.
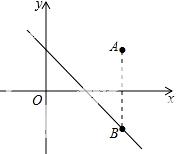
7. 如图,在平面直角坐标系中,点A(2,m)在第一象限,若点A关于x轴的对称点B在直线y=﹣x+1上,则m的值为( )
A. ﹣1 B. 1 C. 2 D. 3

考点:1.一次函数图象上点的坐标特征2.关于x轴、y轴对称的点的坐标.
8. 如图,在 平面直角坐标系中,
平面直角坐标系中, 点A、B均在函数y=
点A、B均在函数y=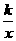 (k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
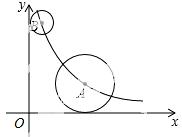
A. (2,2) B. (2,3) C. (3,2) D. (4,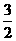 )
)
【答案】C.
【解析】
试题分析:把B的坐标为(1,6)代入反比例函数解析式得:k=6,
则函数的解析式是:y=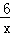 ,
,
∵B的坐标为(1,6),⊙B与y轴相切,
∴⊙B的半径是1,
则⊙A是2,
把y=2代入y=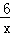 得:x=3,
得:x=3,
则A的坐标是(3,2).
故选C.
考点:1.切线的性质2.反比例函数图象上点的坐标特征.
第Ⅱ卷(非选择题,共96分)
二、填空题(每小题3分,共18分)
9. 计算: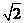 ×
×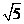 =__________.
=__________.

10. 为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为______元.

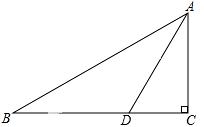
11. 如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为______.
【答案】15.
【解析】
试题分析:作DE⊥AB于E.
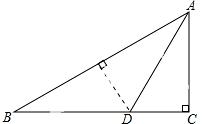
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3.
∴△ABD的面积为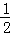 ×3×10=15.
×3×10=15.
故答案是15.
考点:角平分线的性质.
12. 如图,在⊙ O中,半径OA垂直弦于点D.若∠ACB=33°,则∠OBC的大小为______度.
O中,半径OA垂直弦于点D.若∠ACB=33°,则∠OBC的大小为______度.
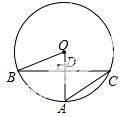

13 . 如图,在边长为3的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为______.
. 如图,在边长为3的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为______.

考点:1.菱形的性质2.相似三角形的判定与性质.
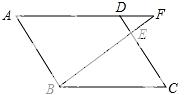
14. 如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B ,对称轴为直线x=﹣2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为______(用含a的式子表示).
,对称轴为直线x=﹣2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为______(用含a的式子表示).
【答案】a+4.
【解析】
试题分析:∵对称轴为直线x=﹣2,抛物线经过原点、 x轴负半轴交于点B,
x轴负半轴交于点B,
∴OB=4,
∵由抛物线的对称性知AB=AO,
∴四边形AOBC的周长为AO+AC+BC+OB=△ABC的周长+OB=a+4.
故答案是a+4.
考点:二次函数的性质.
三、解答题(本大题共10小题,共78分)
15.(6分) 先化简,再求值: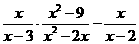 ,其中x=10.
,其中x=10.

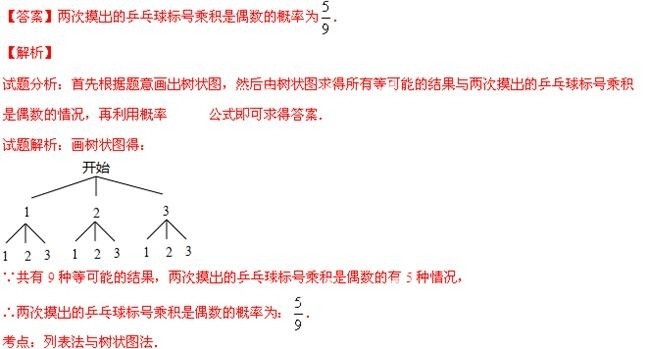
16.(6分) 在一个不透明的袋子里装有3个乒乓球,分别标有数字1,2,3,这些乒乓球除所标数字不同外其余均相同.先从袋子里随机摸出1个乒乓球,记下标号后放回,再从袋子里随机摸出1个乒乓球记下标号,请用画树状图(或列表)的方法,求两次摸出的乒乓球标号乘积是偶数的概率.
17.(6分) 某文具厂计划加工3000套画图工具,为了尽快完成任务,实际每天加工画图工具的数量是原计划的1.2倍,结果提前4天完成任务,求该文具厂原计划每天加工这种画图工具的数量.

18.(7分) 如图,为测量某建筑物的高度AB,在离该建筑物底部24米的点C处,目测建筑物顶端A处,视线与水平线夹角∠ADE为39°,且高CD为1.5米,求建筑物的高度AB.(结果精确到0.1米)(参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81)
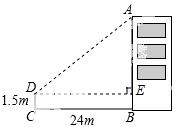
【答案】建筑物的高度AB约为20.9米 .
.
【解析】

∴AB=E+EB=19.44+1.5=20.94≈20.9(米).
答:建筑物的高度AB约为20.9米.
考点:解直角三角形的应用-仰角俯角问题.
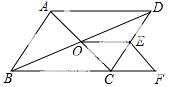
19.(7分) 如图,在▱ABCD中,点O是对角线AC、BD的交 点,点E是边CD的中点,点F在BC的延长线上,且CF=
点,点E是边CD的中点,点F在BC的延长线上,且CF=
 BC,求证:四边形OCFE是平行四边形.
BC,求证:四边形OCFE是平行四边形.
【答案】证明见解析.
【解析】

考点:1.平行四边形的判定与性质2.三角形中位线定理.
20.(7分) 某校学生会为了解本校学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案:
(A)对各班班长进行调查;
(B)对某班的全体学生进行调查;
(C)从全校每班随机抽取5名学生进行调查.
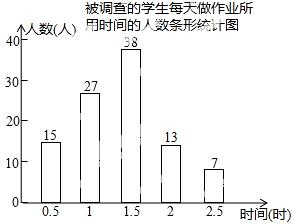
在问卷调查时,每位被调查的学生都选择了问卷中适合自己的一个时间,学生会收集到的数据整理后绘制成如图所示的条形统计图.
(1)为了使收集到的数据具有代表性,学生会在确定调查对象时选择了方案________(填A、B或C);
(2)被调查的学生每天做作业所 用时间的众数为_____小时;
用时间的众数为_____小时;
(3)根据以上统计结果,估计该校800名学生中每天做作业用1.5小时的人数.

考点:1.条形统计图2.抽样调查的可靠性3.用样本估计总体4.众数.
21.(8分) 甲、乙两支清雪队同时开始清理某路段积雪,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的清 雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨)
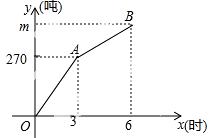
雪任务,已知甲队每小时的清雪量保持不变,乙队每小时清雪50吨,甲、乙两队在此路段的清雪总量y(吨) 与清雪时间x(时)之间的函数图象如图所示.
与清雪时间x(时)之间的函数图象如图所示.
(1)乙队调离时,甲、乙两队已完成的清雪总量为_____吨;
(2)求此次任务的清雪总量m;
(3)求乙队调离后y与x之间的函数关系式.
【答案】(1)270;
(2)此次任务的清雪总量为390吨;
(3)乙队调离后y与x之间的函数关系式:y=40x+150.
【解析】

∴乙队调离后y与x之间的函数关系式:y=40x+15 0.
0.
考点:一次函数的应用.
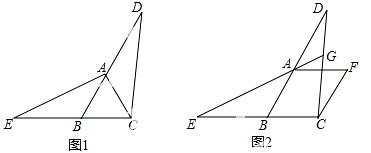
22.(9分) 探究:如图①,在△ABC中,AB=AC,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,AE,求证:△ACE≌△CBD.
应用:如图②,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB 至点E,使BE=AD,连结CD,EA,延长EA交CD于点G,求∠CGE的度数.
至点E,使BE=AD,连结CD,EA,延长EA交CD于点G,求∠CGE的度数.
【答案】探究:证明见解析;
应用:∠CGE=60°.
【解析】

∴△ACE≌△CBD(SAS);
应用:如图,连接AC,易知△ABC是等边三角形,
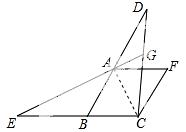
由探究可知△ACE≌△CBD,
∴∠E=∠D,
∵∠BAE=∠DAG,
∴∠E+∠BAE=∠D+∠DAG,
∴∠CGE=∠ABC,
∵∠ABC=60°,
∴∠CGE=60°.
考点:1.全等三角形的判定与性质2.等边三角形的判定与性质3.菱形的性质.
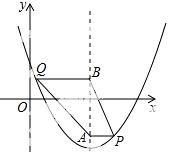
23.(10分) 如图,在平面直角坐标系中,抛物线y=x2+bx +c经过点(1,﹣1),且对称轴为在线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.
+c经过点(1,﹣1),且对称轴为在线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.
(1)求这条抛物线所对应的函数关系式;
(2)求点Q的坐标(用含m的式子表示);
(3)请探究PA+Q B=AB是否成立,并说明理由;
B=AB是否成立,并说明理由;
(4 )抛物线y=a1x2+b1x+c1(a1≠0)经过Q、B、P三点,若其对称轴把四边形PAQB分成面积为1:5的两部分,直接写出此时m的值.
)抛物线y=a1x2+b1x+c1(a1≠0)经过Q、B、P三点,若其对称轴把四边形PAQB分成面积为1:5的两部分,直接写出此时m的值.

(4)根据抛物线的对称性,抛物线y=a1x2+b1x+c1的对称轴为QB的垂直平分线,然后根据四边形PAQB被分成的两个部分列出方程求解即可.
试题解析:(1)∵抛物线y=x2+bx+c经过点(1,﹣1),且对称轴为在线x=2,
∴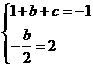 ,
,
解得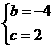 .
.

∴PA+QB=AB;
(4)∵抛物线y=a1x2+b1x+c1(a1≠0)经过Q、B、P三点,
∴抛物线y=a1x2+b1x+c1的对称轴为QB的垂直平分线,
∵对称轴把四边形PAQB分成面积为1:5的两部分,
∴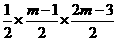 =
=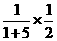 (2m﹣3)×(2m﹣3),
(2m﹣3)×(2m﹣3),
整理得,(2m﹣3)(m﹣3)=0,
∵点P位于对称轴右侧,
∴m>2,
∴2m﹣3≠0,
∴m﹣3=0,
解得m=3.
考点:二次函数综合题.
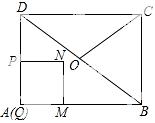
24.(12分) 如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)求点N落在BD上时t的值;
(2)直接写出点O在正方形PQMN内部时t的取值范围;
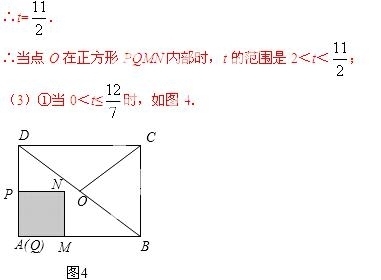
(3 )当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;
)当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;
(4)直接写出直线DN平分△BCD面积时t的值.
【答案】(1)当t=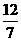 时,点N落在BD上;
时,点N落在BD上;
(2)当点O在正方形PQMN内部时,t的范围是2<t<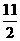 ;
;
(3)当0<t≤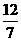 时,S=t2.
时,S=t2.

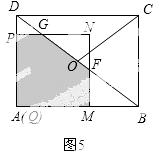
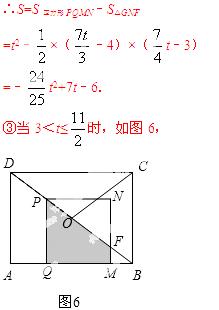
(3)根据正方形PQMN与△ABD重叠部分图形形状不同 分成三类,如图4、图5、图6,然后运用三角形相似、锐角三角函数等知识就可求出S与t之间的函数关系式;
分成三类,如图4、图5、图6,然后运用三角形相似、锐角三角函数等知识就可求出S与t之间的函数关系式;
(4)由于点P在折线AD﹣DO﹣OC运动,可分点P在AD上,点P在DO上,点P在OC上三种 情况进行讨论,然后运用三角形相似等知识就可求出直线DN平分△
情况进行讨论,然后运用三角形相似等知识就可求出直线DN平分△ BCD面积时t的值.
BCD面积时t的值.
试题解析:(1)当点N落在BD上时,如图1.
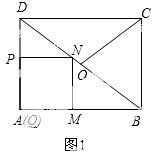
∵四边形PQMN是正方形,
∴PN∥QM,PN=PQ=t.
∴△DPN∽△DQB.
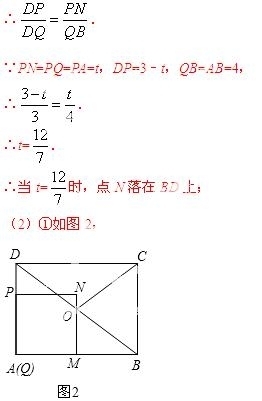
则有QM=QP=t,MB=4﹣t.
∵四边形PQMN是正方形,
∴MN∥DQ.
∵点O是DB的中点,
∴QM=BM.
∴∠A=90°.
∵AB=4,AD=3,
∴DB=5.
∵点O是DB的中点,
∴DO=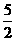 .
.
∴1×t=AD+DO=3+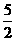 .
.
S=S正方形PQMN=PQ2=PA 2=t2.
2=t2.
②当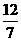 <t≤3时,如图5,
<t≤3时,如图5,
∵tan∠ADB=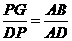 ,
,
∴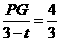 .
.
∴PG=4﹣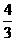 t.
t.
∴GN=PN﹣PG=t﹣(4﹣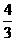 t)=
t)=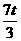 ﹣4.
﹣4.
∵tan∠NFG=tan∠ADB=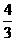 ,
,
∴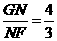 .
.
∴NF=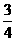 GN=
GN=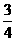 (
(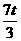 ﹣4)=
﹣4)=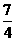 t﹣3.
t﹣3.
∵四边形 PQMN是正方形,四边形ABCD是矩形.
PQMN是正方形,四边形ABCD是矩形.
∴∠PQM=∠DAB=90°.
∴PQ∥AD.
∴△BQP∽△BAD.
∴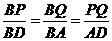 .
.
∵BP=8﹣t,BD=5,BA=4,AD=3,
∴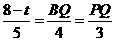 .
.
∴BQ=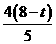 ,PQ=
,PQ=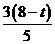 .
.

当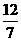 <t≤
<t≤ 3时,S=﹣
3时,S=﹣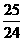 t2+7t﹣6.
t2+7t﹣6.
当3<t≤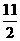 时,S=
时,S=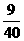 t2﹣
t2﹣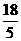 t+
t+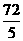 ;
;
(4)设直线DN与BC交于点E,
∵直线DN平分△BCD面积,
∴BE=CE=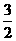 .
.
①点P在AD上,过点E作EH∥PN交AD于点H,如图7,
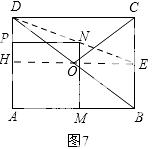
则有△DPN∽△DHE.
∴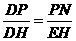 .
.
∵PN=PA=t,DP=3﹣t,DH=CE=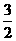 ,EH=AB=4,
,EH=AB=4,
∴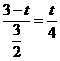 .
.
∵PQ=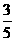 (8﹣t),PN=PQ,
(8﹣t),PN=PQ,
∴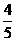 (t﹣3)=
(t﹣3)=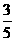 (8﹣t).
(8﹣t).
解得:t=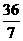 .
.
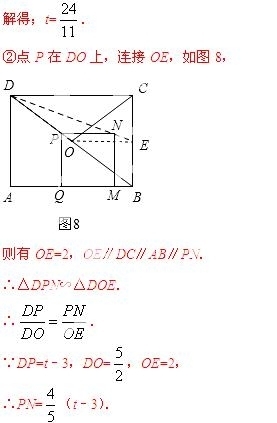
③点P在OC上,设DE与OC交于点S,连接OE,交PQ于点R,如图9,
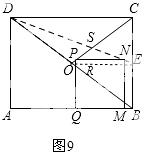
则有OE=2,OE∥DC.
∴△DSC∽△ESO.
∴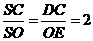 .
.
∴SC=2SO.
∵OC=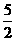 ,
,

∴PR=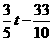 .
.
∵QR=B E=
E=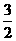 ,
,
∴PQ=PR+QR=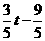 .
.
∵PN=PQ,
∴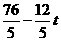 =
=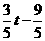 .
.
解得:t=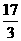 .
.
综上所述:当直线DN平分△BCD面积时,t的值为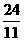 、
、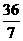 、
、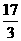 .
.
考点:相似形综合题.


