(单词翻译:单击)
一、选择题
1.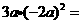 ( )
( )
A.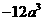 B.
B. 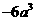 C.
C. 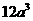 D.
D. 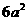
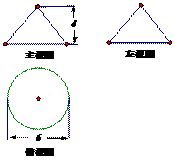
2. 已知某几何体的三视图( 单位:cm)则该几何体的侧面积等于( )
单位:cm)则该几何体的侧面积等于( )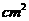
A. 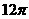 B.
B. 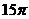 C.
C. 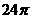 D.
D. 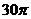
3.在RT△ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A. 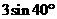 B.
B. 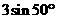 C.
C. 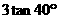 D.
D. 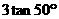
4.已知边长为a的正方形面积为8,则下列关于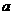 的说法中,错误的是( )
的说法中,错误的是( )
A. a是无理数 B. a是方程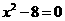 的解
的解
C. a是8的 算术平方根 D. a满足不等式组
算术平方根 D. a满足不等式组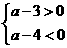
5.下列命题中,正确的是( )
A .梯形的对角线相等 B. 菱形的对角线不相等
C. 矩形的对角线不能互相垂直 D. 平行四边想的对角线可以互相垂直
6. 函数的自变量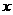 满足
满足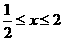 时,函数值
时,函数值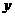 满足
满足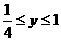 ,则这个函数可以是( )
,则这个函数可以是( )
A. 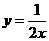
 B.
B. 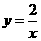 C.
C. 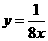 D.
D. 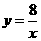
7. 若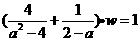 ,则w=( )
,则w=( )
A.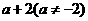 B.
B. 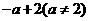 C.
C. 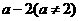 D.
D. 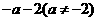
8. 已知2001年至2012年杭州市小学学校数量(单位:所)和在校学生人数(单位:人)的两幅统计图,由图得出如下四个结论:
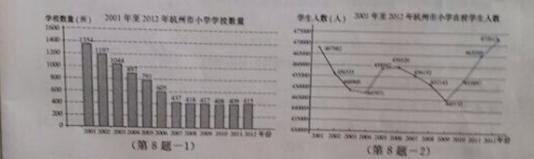
①学校数量2007至2012年比2001至2006年更稳定;
②在校学生人数有两次连续下降,两次连续增长的变化过程;
③2009年的 大于1000;
大于1000;
④2009~2012年,各相邻两年的学校数量增长和在校学生人数增长最快的都是2011~2012年.
其中,正确的结论是( )
A. ①②③④ B. ①②③ C. ①②③ D.③④
9. 让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和是2的倍数或是3的倍数的概率等于( )
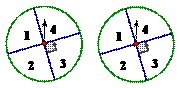
A.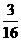 B.
B. 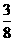 C.
C. 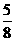 D.
D.
10.已知AD//BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
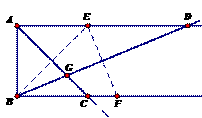
A. 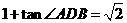 B.
B. 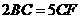
C. 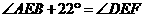 D.
D. 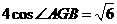
二、填空题
11. 2012年末统计,杭 州市常住人口是880.2万人,用科学技术法表示为____________.
州市常住人口是880.2万人,用科学技术法表示为____________.
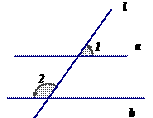
12. 已知直线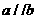 ,若∠1=40°50′,则∠2= ___________.
,若∠1=40°50′,则∠2= ___________.
13. 设实数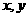 满足方程组
满足方程组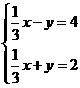 ,则
,则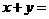 ___________.
___________.
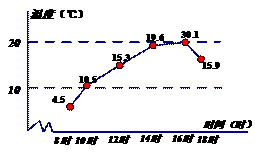
14.已知杭州市某天六个整点时的气温绘制成的统计图,则这六个整点时气温的中位数 是___________.
是___________.
15.设抛物线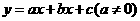 过A(0,2), B(4,3),C三点,其中点C在直线
过A(0,2), B(4,3),C三点,其中点C在直线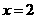 上,且点C到抛物线对称轴的距离等于1,则抛物线的函数解析式为___________.
上,且点C到抛物线对称轴的距离等于1,则抛物线的函数解析式为___________.
16. 点A,B,C都在半径为 的圆上,直线AD⊥直线BC,垂足为D,直线BE⊥直线AC,垂足为E,直线AD与BE相交于点H,若
的圆上,直线AD⊥直线BC,垂足为D,直线BE⊥直线AC,垂足为E,直线AD与BE相交于点H,若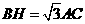 ,则∠ABC所对的弧长等于___________(长度单位).
,则∠ABC所对的弧长等于___________(长度单位).
三、解答题
17. 一个布袋中装有只有颜色不同的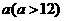 个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整),请补全该统计图并求出
个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整),请补全该统计图并求出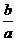 的值。
的值。
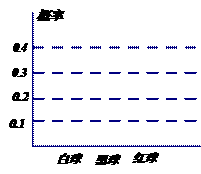
18. 在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,求证:PB=PC,并请直接写出图中其他相等的线段。
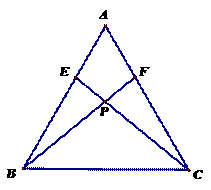
19. 设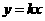 是否存在实数
是否存在实数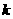 ,使得代数式
,使得代数式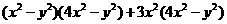 能化简为
能化简为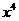 ?若能,请求出所有满足条件的
?若能,请求出所有满足条件的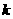 值,若不能,请说明理由。
值,若不能,请说明理由。
20. 把一条12个单位长度的线段分成三条线段,其中一条线段长为4个单位长度,另两条线段长都是单位长度的整数倍。
(1)不同分法得到的三条线段能组成多少个不全等的三角形?用尺规作出这些三角形(用给定的单位长度,不写作法,保留作图痕迹 );
);
(2)求出(1)中所作三角形外接圆的周长。
21. 在直角坐标系中,设x轴为直线l,函数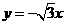 ,
,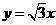 的图像分别是
的图像分别是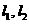 ,半径为1的
,半径为1的 与直线
与直线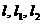 中的两条相切,例如
中的两条相切,例如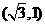 是其中一个
是其中一个 的圆心坐标。
的圆心坐标。
(1) 写出其余满足条件的
写出其余满足条件的 的圆心坐标;
的圆心坐标;
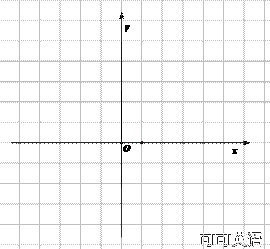
(2)在图中标出所有圆心,并用线段依次连结各圆心,求所得几何图形的周长(该题问法不严密)。
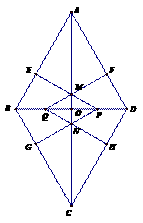
22.菱形ABCD的对角线AC,BD相交于点O,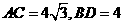 ,动点P在线段BD上从点B向点D运动,PP′⊥AB于点P′,四边形PFBG关于BD对称。四边形QEDH与四边形PFBG关于AC对称,设菱形ABCD被这两个四边形盖住部分的面积为
,动点P在线段BD上从点B向点D运动,PP′⊥AB于点P′,四边形PFBG关于BD对称。四边形QEDH与四边形PFBG关于AC对称,设菱形ABCD被这两个四边形盖住部分的面积为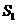 ,未盖住部分的面积为
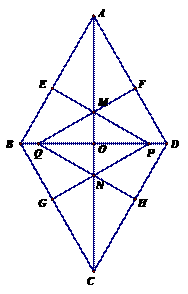
,未盖住部分的面积为 ,
,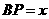 .
.
(1)用含x代数式分别表示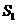
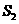 ;
;
(2 )若
)若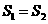 ,求x.
,求x.
23.复习课中,教师给出关于x的函数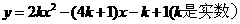 .
.
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写道黑板上.
学生思考后,黑板上出现了一些结论,教师作为活动医院,又补充一些结论,并从中选择如下四条:
①存在函数,其图像经过(1,0)点;
②函数图像与坐标轴总有三个不同的交点;
③当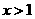 时,
时, 不是y随x的增大而增大就是y随x的增大而减小;
不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数。
教师:请你分别判断四条结论的真假,并给出理由.最后简单写出解决问题时所用的数学方法。
数学卷参考答案
一、选择题
1. C 2、B 3、D 4、D 5、D 6、A 7、D 8、B 9、C 10、A
二、填空题
11. 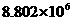
12. 139°10′.
13. 8 .
14. 15.6 .
15. 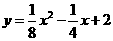 或
或 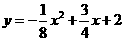 .
.
16. 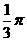 或
或 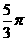
三、解答题
17. 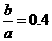
18、证明:因为AB=AC,所以,∠ABC=∠ACB,
又因为AE=AF,∠A=∠A,所以,ΔABF≌ΔACE,
所以,∠ABF=∠ACE,所以,∠PBC=∠PCB,所以,PB=PC
相等的线段还有BF=CE,PF=PE,BE=CF
19. 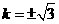 或
或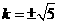
20. (1)3,4,5;4,4,4;
(2)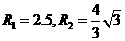
21. (1)分两类,利用对称求解:
①相邻直线对称轴
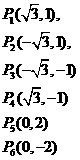
②不相邻直线对称轴
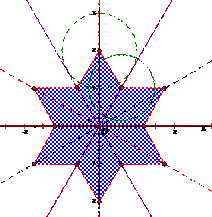
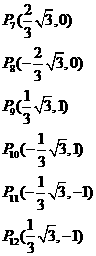 除
除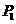 外余11点。
外余11点。
(2)一边为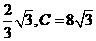 。
。
22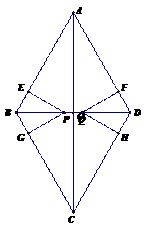 、解:(1)①当
、解:(1)①当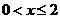
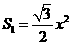 ,
,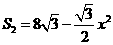
②当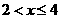
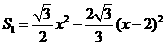 ,
,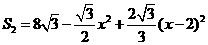
(不化简更实用)
 (2)①当
(2)①当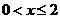 得:
得:
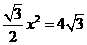 得:
得: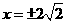 (舍去);
(舍去);
②当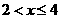 得:
得: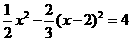
解得: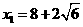 (舍去),
(舍去),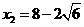
∴当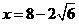 。
。
23.解:①真,代入得: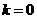 ;数形结合?方程思想?
;数形结合?方程思想?
②假,反例如: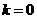 ;特殊与一般?举反例
;特殊与一般?举反例
③假 ,如
,如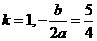 ,当
,当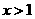 时,先减后增;举反例,特殊一般?
时,先减后增;举反例,特殊一般?
④真,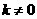 ,记:
,记: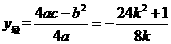 ,
,
∴当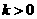 时,有最小值,最小值为负;
时,有最小值,最小值为负;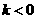 时,有最大值,最大值为正。
时,有最大值,最大值为正。


