(单词翻译:单击)
一、选择题(本大题共8小题,每小题3 分,共24分)每小题只有一个准确选项
分,共24分)每小题只有一个准确选项
1. -7的相反数是
A. -7 B. 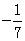 C.
C. 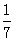 D. 7
D. 7
2. 下列安全标志图中,是中心对称图形的是

A. B. C. D.
3. 下列运算准确的是

4. 抚州名人雕塑园是国家4A级旅游景区,占地面积约560000m2,将560000用科学记数法表示应为
A. 0.56×106 B. 5.6×106 C. 5.6×10 5 D. 56×104
5. 某运动器材的形状如图所示,以箭头所指的方向为左视方向,则它的主视图可以是

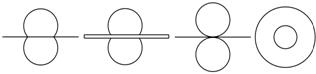
A. B. C. D.
6. 已知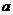 、
、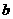 满足方程组
满足方程组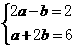 ,则
,则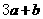 的值为
的值为
A. 8 B. 4 C. -4 D. -8
7. 为了解某小区小孩暑假的学习情况, 王老师随机调查了该小区8个小孩某天的学习时间,结果如下 (单位:小时):1.5 ,1.5 ,3 ,4,2 ,5 ,2.5 ,4.5.关于这组数据,下列结论错误的是
王老师随机调查了该小区8个小孩某天的学习时间,结果如下 (单位:小时):1.5 ,1.5 ,3 ,4,2 ,5 ,2.5 ,4.5.关于这组数据,下列结论错误的是
A. 极差是3.5 B. 众数是1.5 C. 中位数是3 D.平均数是3
8. 一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍, 其主视图如图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是
其主视图如图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是
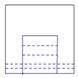

A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分.请把准确的答案填写在答题卷相应位置的横线上)
9. 计算: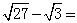 ____________ .
____________ .
10. 因式分解:a3-4a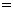 ___________.
___________.
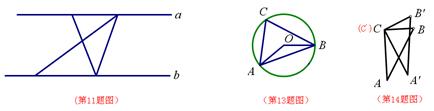
11. 如图,a∥b ,∠1+∠2=75°,则∠3+∠4= ___________°.
12. 关于x的一元二次方程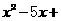 k=0有两个不相等的实数根,则k可取的最大整数为___________ .
k=0有两个不相等的实数根,则k可取的最大整数为___________ .
13. 如图,△ABC内接于⊙O ,∠OAB=20°,则∠C的度数为 _____________.
14. 如图,两块完全相同的含30°角的直角三角板ABC和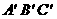 重合在一起,将三角板
重合在一起,将三角板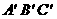 绕其顶点
绕其顶点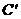 按逆时针方向旋转角α(0°< α≤90°),有以下四个结论:
按逆时针方向旋转角α(0°< α≤90°),有以下四个结论:
①当α=30°时,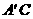 与
与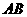 的交点恰好为
的交点恰好为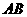 的中点;②当α=60°时,
的中点;②当α=60°时,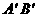 恰好经过点
恰好经过点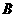 ;
;
③在旋转过程中,存在某一时刻,使得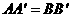 ; ④在旋转过程中,始终存在
; ④在旋转过程中,始终存在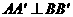 ,其中结论正确的序号是______________.(多填或填错得0分,少填酌情给分)
,其中结论正确的序号是______________.(多填或填错得0分,少填酌情给分)
三、( 本大题共2小题,每小题5分,共10分)
本大题共2小题,每小题5分,共10分)
15. 如图,△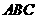 与△
与△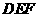 关于直线
关于直线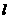 对称,请用无刻度的直尺,在下面两个图中分别作出直线
对称,请用无刻度的直尺,在下面两个图中分别作出直线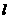 .
.
16. 先化简: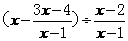 ,再任选一个你喜欢的数
,再任选一个你喜欢的数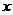 代入求值.
代入求值.
四、(本大题共2小题,每小题7分,共14分)
17. 某同学报名参加运动会,有以下5个项目可供选择:径赛项目:100m ,200m ,400m(分别用A1 、A2 、A3表示);田赛项目:跳远 ,跳高(分别用B1 、B2表示).
⑴ 该同学从5个项目中任选一个,恰好是田赛项目的概率为_____________;
⑵ 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能 出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
18. 如图,在平面直角坐标系中,过点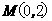 的直线
的直线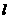 与
与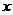 轴平行,且直线
轴平行,且直线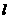 分别与反比例函数
分别与反比例函数 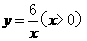 和
和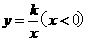 的图象交于点
的图象交于点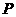 、点
、点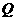 .
.
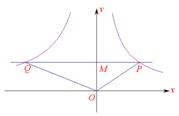
⑴ 求点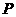 的坐标;
的坐标;
⑵ 若△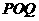 的面积为8 ,求k的值 .
的面积为8 ,求k的值 .
五、(本大题共2小题,每小题8分,共16分)
19. 情景:

试根据图中的信息,解答下列问题:
⑴ 购买6根跳绳需__________元,购买12根跳绳需__________元.
⑵ 小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红 __________购 买跳绳的根数;若没有,请说明理由.
买跳绳的根数;若没有,请说明理由.
20. 某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
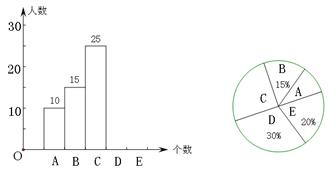
组别 | 听写正确的 个数x | 组中值 |
A | 0≤x<8 | 4 |
B | 8≤x<16 | 12 |
C | 16≤x<24 | 20 |
D | 24≤x<32 | 28 |
E | 32≤x<40 | 36 |
根据以上信息解决下列问题:
⑴ 本次共随机抽查了__________名学生,并补全条形统计图;
⑵ 若把每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确的个数的平均数是多少?
⑶ 该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
六、(本大题共2小题,每小题9分,共18分)
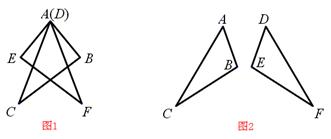
21. 如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2.晾衣架伸缩时,点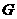 在射线
在射线 
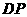 上滑动,∠
上滑动,∠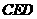 的大小也随之发生变化.已知每个菱形边长均等于20cm ,且
的大小也随之发生变化.已知每个菱形边长均等于20cm ,且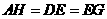 =20cm .
=20cm .

⑴ 当∠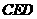 =60°时,求
=60°时,求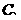
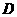 两点间的距离;
两点间的距离;
⑵ 当∠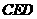 由60°变为120°时,点
由60°变为120°时,点 向左移动了多少cm ?(结果精确到0.1cm)
向左移动了多少cm ?(结果精确到0.1cm)
⑶ 设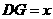 cm ,当∠
cm ,当∠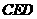 的变化范围为60°~ 120°(包括端点值)时,求
的变化范围为60°~ 120°(包括端点值)时,求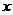 的取值范围 .(结果精确到0.1cm) (参考数据:
的取值范围 .(结果精确到0.1cm) (参考数据: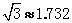 ,可使用科学计算器)
,可使用科学计算器)
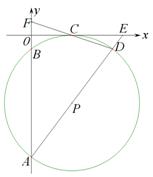
22. 如图,在平面直角坐标系中,⊙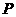 经过
经过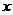 轴上一点
轴上一点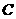 ,与y轴
,与y轴 分别交于
分别交于 、
、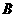 两点,连接
两点,连接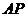 并延长分别交⊙
并延长分别交⊙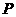 、
、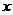 轴于点
轴于点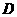 、
、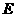 ,连接
,连接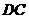 并延长交y轴于点
并延长交y轴于点 ,若点
,若点 的坐标为(0 ,1)
的坐标为(0 ,1) ,点
,点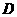 的坐标为(6 ,-1).
的坐标为(6 ,-1).
⑴ 求证: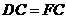
⑵ 判断⊙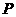 与
与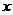 轴的位置关系,并说明理由.
轴的位置关系,并说明理由.
⑶ 求直线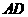 的解析式.
的解析式.
七、(本大题共2小题,每小题10分,共20分)
23. 如图,抛物线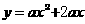 (
(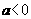 )位于
)位于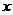 轴上方的图象记为
轴上方的图象记为 1 ,它与
1 ,它与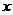 轴交于
轴交于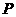 1 、
1 、 两点,图象
两点,图象 2与
2与 1关于原点
1关于原点 对称,
对称,  2与
2与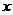 轴的另一个交点为
轴的另一个交点为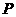 2 ,将
2 ,将 1与
1与 2同时沿
2同时沿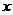 轴向右平移
轴向右平移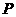 1
1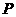 2的长度即可得
2的长度即可得 3与
3与 4 ;再将
4 ;再将 3与
3与 4 同时沿
4 同时沿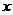 轴向右平移
轴向右平移 1
1 2的长度即可得
2的长度即可得 5与
5与 6 ;
6 ;
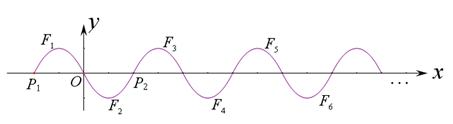
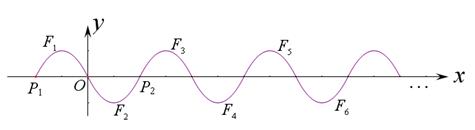
……按这样的方式一直平移下去即可得到一系列图象 1 ,
1 , 2 ,…… ,
2 ,…… , n ,我们把这组图象称为“波浪抛物线”.
n ,我们把这组图象称为“波浪抛物线”.
⑴ 当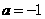 时,
时,
① 求图象 1的顶点坐标;
1的顶点坐标;
② 点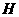 (2014 , -3)_______(填“在”或“不在”)该“波浪抛物线”上;若图象
(2014 , -3)_______(填“在”或“不在”)该“波浪抛物线”上;若图象 n 的顶点
n 的顶点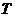 n对应的解析式为______________,其自变量
n对应的解析式为______________,其自变量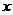 的取值范围为______________.
的取值范围为______________.
⑵ 设图象 m、
m、 m+1的顶点分别为
m+1的顶点分别为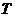 m 、
m 、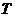 m+1 (m为正整数),
m+1 (m为正整数),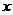 轴上一点Q的坐标为(12 ,0).试探究:当
轴上一点Q的坐标为(12 ,0).试探究:当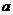 为何值时,以
为何值时,以 、
、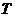 m 、
m 、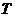 m+1、Q四点为顶点的四边形为矩形?并直接写出此时m的值.
m+1、Q四点为顶点的四边形为矩形?并直接写出此时m的值.
24.【试题背景】
已知: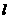 ∥
∥ ∥
∥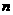 ∥
∥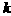 ,平行线
,平行线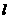 与
与 、
、 与
与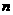 、
、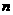 与
与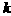 之间的距离分别为
之间的距离分别为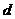 1、
1、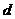 2、
2、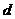 3,且
3,且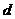 1 =
1 =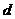 3 = 1,
3 = 1,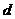 2 = 2 . 我们把四个顶点分别在
2 = 2 . 我们把四个顶点分别在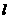 、
、 、
、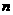 、
、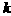 这四条平行线上的四边形称为“格线四边形”.
这四条平行线上的四边形称为“格线四边形”.
【探究1】 ⑴ 如图1,正方形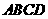 为“格线四边形”,
为“格线四边形”,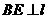 于点
于点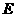 ,
,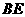 的反向延长线交直线
的反向延长线交直线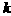 于点
于点 . 求正方形
. 求正方形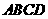 的边长.
的边长.
【探究2】 ⑵ 矩形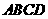 为“格线四边形”,其长 :宽 = 2 :1 ,则矩形
为“格线四边形”,其长 :宽 = 2 :1 ,则矩形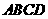 的宽为____________.
的宽为____________.
(直接写出结果即可)
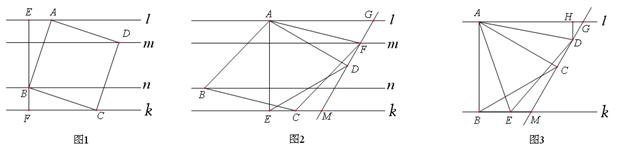
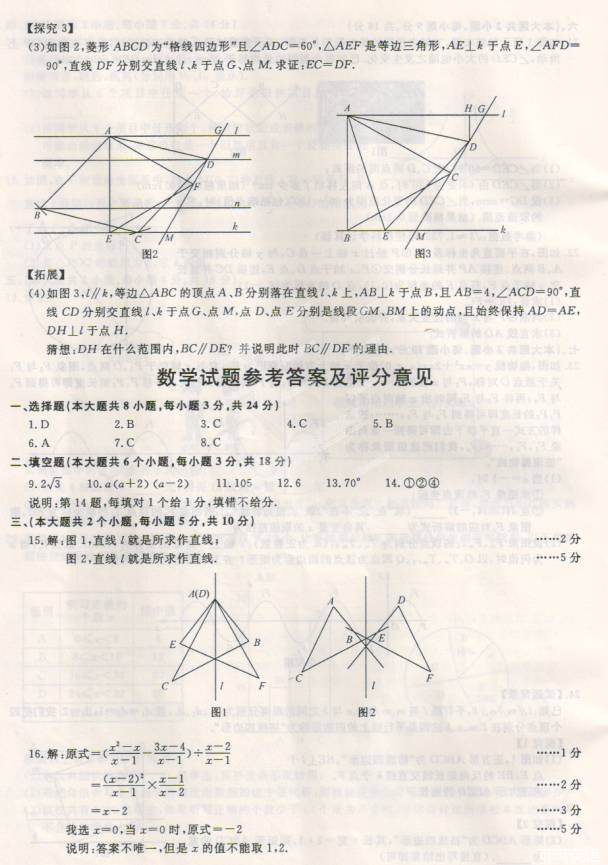
【探究3】 ⑶ 如图2,菱形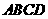 为“格线四边形”且∠
为“格线四边形”且∠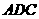 =60°,△
=60°,△ 是等边三角形,
是等边三角形,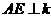 于点
于点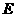 , ∠
, ∠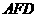 =90°,直线
=90°,直线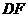 分别交直线
分别交直线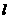 、
、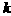 于点
于点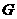 、
、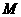 . 求证:
. 求证: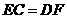 .
.
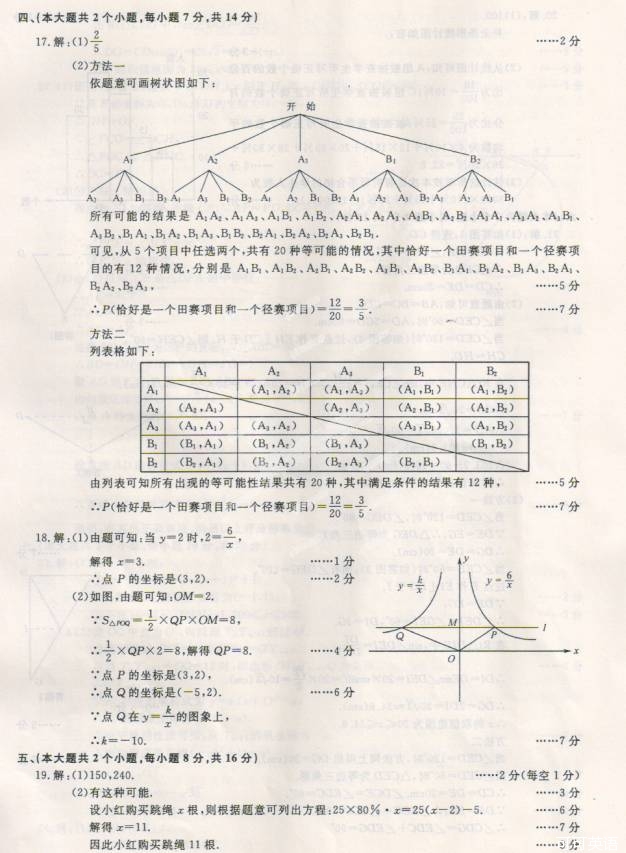
【拓 展】 ⑷ 如图3,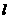 ∥
∥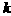 ,等边三角形
,等边三角形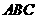 的顶点
的顶点 、
、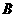 分别落在直线
分别落在直线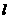 、
、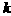 上,
上,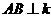 于点
于点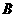 ,且
,且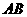 =4 ,∠
=4 ,∠ =90°,直线
=90°,直线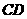 分别交直线
分别交直线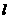 、
、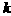 于点
于点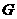 、
、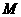 ,点
,点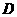 、
、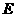 分别是线段
分别是线段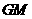 、
、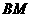 上的动点,且始终保持
上的动点,且始终保持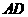 =
=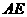 ,
,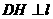 于点
于点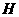 .
.
猜想: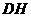 在什么范围内,
在什么范围内,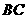 ∥
∥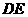 ?并说明此时
?并说明此时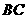 ∥
∥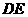 的理由.
的理由.